Math 119 Chap 6 part 1

Brad Bolton
14 Dec 202017:05
EducationalLearning
32 Likes 10 Comments

TLDRThis instructional video introduces Chapter Six, focusing on normal distribution in statistics. The instructor explains the concept of a normal distribution, its attributes like symmetry and bell shape, and the significance of the total area under the curve equating to one. Emphasizing the use of calculators for complex calculations, the video demonstrates how to find probabilities using z-scores and the normal cumulative distribution function (normalcdf) on a TI-84 Plus calculator. The session includes practical examples to help students understand the calculation of probabilities for z-scores being less than, greater than, or between specific values.

Takeaways
  • 🎥 The video is an introduction to Chapter 6 of a course, focusing on normal distribution and z-scores.
  • 🕒 The video is expected to be around 20 to 30 minutes long to help students get accustomed to the format.
  • 📈 The instructor emphasizes the importance of the normal distribution's symmetric, bell-shaped graph and its formula involving 'e to the power of...'.
  • 📊 The total area under the normal distribution curve equals one, representing 100%, which is crucial for understanding probabilities.
  • 📚 Students are advised to have chapters 1 through 6 printed out for reference during the video.
  • 📉 The empirical rule is mentioned as a method for approximating probabilities in a normal distribution, with the 68-95-99.7 percentages.
  • 🔢 The standard normal distribution is defined with a mean (mu) of zero and a standard deviation (sigma) of one.
  • ⚖️ Z-scores are explained as a measure of relative standing in comparison to the mean, indicating how many standard deviations away from the mean a value is.
  • 🧮 The use of a calculator, specifically the 'normalcdf' function on a TI-84 Plus, is highlighted for finding probabilities associated with z-scores.
  • 📝 The instructor provides step-by-step instructions on how to use the calculator for different probability scenarios involving z-scores.
  • 🔍 The video script includes practical examples of calculating probabilities for z-scores being less than, greater than, and between certain values.
Q & A

  • What is the main focus of the first video from chapter six?

    -The main focus of the first video is to introduce the concept of normal distribution, its attributes, and the use of calculators for calculations related to it.

  • What are the key attributes of a normal distribution mentioned in the script?

    -The key attributes of a normal distribution are that it is symmetric, has a single peak (one mode), is bell-shaped, and the total area under the curve equals one (100%).

  • Why is the formula for a normal distribution not a primary concern in this context?

    -The formula for a normal distribution is not a primary concern because the calculations will be done using a calculator, emphasizing the understanding of the distribution's characteristics and the use of technology for computation.

  • What is the empirical rule and how does it relate to the normal distribution?

    -The empirical rule is a way to approximate probabilities of a normal distribution using the percentages 68%, 95%, and 99.7%, which represent the area under the curve within one, two, and three standard deviations from the mean, respectively.

  • What is a z-score and how does it relate to the standard normal distribution?

    -A z-score indicates the relative standing of a data point compared to the mean, measured in terms of standard deviations. In the context of the standard normal distribution, a z-score always has a mean of zero and a standard deviation of one.

  • What is the purpose of the normalcdf function on the calculator?

    -The normalcdf function on the calculator is used to find the cumulative distribution function (CDF) for a normal distribution, which helps in determining the probability of a z-score being less than, greater than, or between certain values.

  • How does the instructor plan to handle office hours for the course?

    -The instructor plans to have set times for office hours, where students can discuss parts of the course they didn't understand, presumably through the Zoom platform.

  • What is the significance of the area under the normal density curve in terms of probabilities?

    -The area under the normal density curve represents the probability of a particular event occurring. Since the total area is one (or 100%), it allows for the discussion of probabilities in terms of the area under the curve.

  • What is the standard normal distribution and why is it important?

    -The standard normal distribution is a normal distribution with a mean (mu) of zero and a standard deviation (sigma) of one. It is important because it serves as a basis for comparing other normal distributions and for calculating probabilities using z-scores.

  • How does the instructor plan to approach the teaching of z-scores in the course?

    -The instructor plans to focus heavily on z-scores, teaching how to interpret them in the context of a normal distribution as probabilities, and how to calculate them using the formula x minus mu over the standard deviation.

  • What is the formula for calculating a z-score mentioned in the script?

    -The formula for calculating a z-score is (x - mu) / sigma, where x is the data point, mu is the mean, and sigma is the standard deviation.

Outlines
00:00
📚 Introduction to Chapter Six and Normal Distribution

The instructor begins the first video of Chapter Six, introducing the format of 20-30 minute videos and the plan for office hours to discuss any difficulties. The main focus is on the normal distribution, characterized by its symmetric, bell-shaped graph and the formula involving 'e to the power of...'. The instructor emphasizes the importance of the area under the curve representing probabilities and the attributes of a normal distribution, such as being symmetric, having a single peak, and the total area equating to one. The standard normal distribution is also introduced with its specific parameters (mean=0, standard deviation=1) and the concept of z-scores for measuring relative standing to the mean.

05:00
🔢 Calculator Steps for Finding Probabilities of Z-Scores

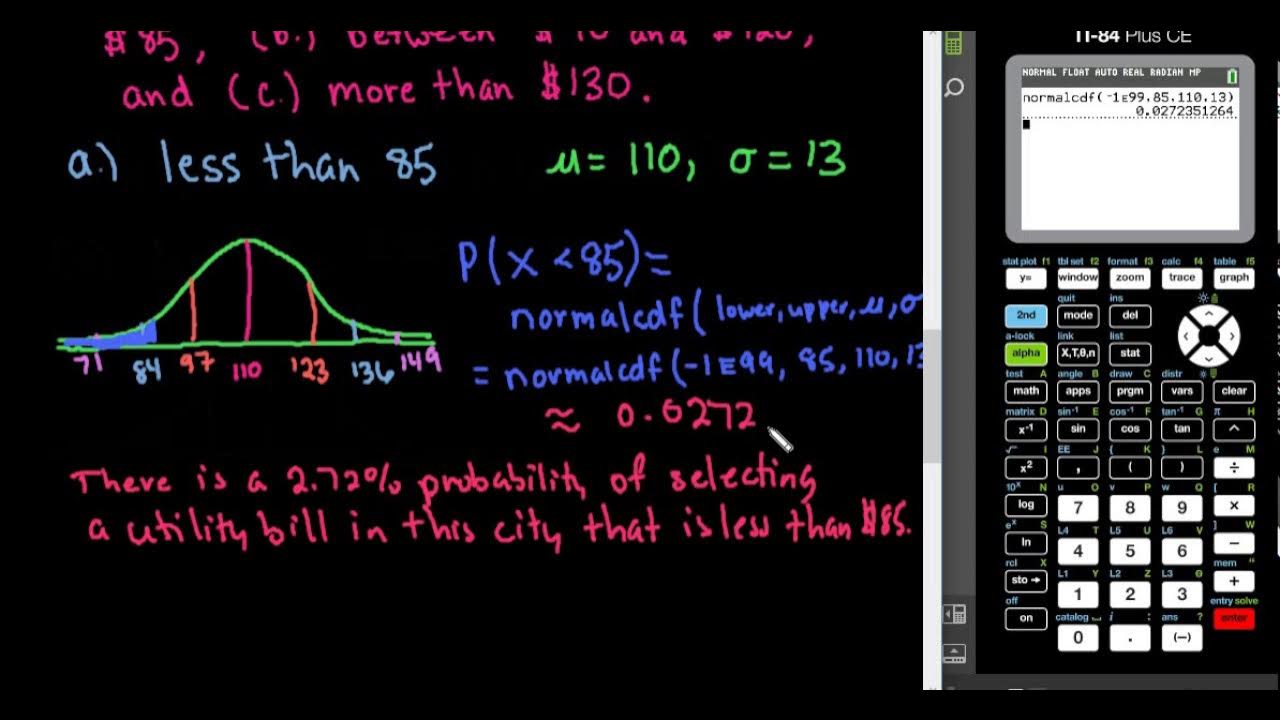
The instructor explains the process of using a calculator, specifically the TI-84 Plus, to find probabilities associated with z-scores. The focus is on using the 'normalcdf' function, which calculates the cumulative distribution function for the normal distribution. The video demonstrates how to find the probability of a z-score being less than a certain value by setting the lower bound to a very negative number and the upper bound to the z-score of interest. The example provided calculates the probability of a z-score being less than -2.16, resulting in approximately 0.0154.

10:01
📉 Understanding Z-Score Probabilities and Empirical Rule

The video continues with the calculation of probabilities for z-scores greater than a certain value and the probability of a z-score falling between two values. The instructor uses the empirical rule, which approximates probabilities based on the standard normal distribution, and the concept of z-scores to explain the calculations. The example for part b calculates the probability of a z-score being greater than 3.09, which is found to be very small, approximately 0.001. The instructor also discusses the importance of visualizing the z-scores on the normal distribution curve to understand the areas and probabilities better.

15:06
📝 Conclusion and Homework Preview

The instructor wraps up the video by summarizing the key points covered, including using calculators to find areas to the right, left, or in between two z-scores on the normal distribution curve. The video serves as an introduction to the homework, which will be posted soon, and encourages students to practice the examples provided. The instructor also reassures students that they will become more comfortable with the process as they continue with the course and looks forward to further discussions on Monday.

Mindmap
Keywords
💡Normal Distribution
A normal distribution, also known as Gaussian distribution, is a probability distribution that is characterized by its symmetric bell-shaped curve. In the context of the video, it is used to describe a continuous random variable with a specific formula, e^(-(x^2)/2), which is central to the study of statistics. The video emphasizes that the area under the curve represents probabilities, with a total area of one, indicating that it encompasses all possible outcomes.
💡Calculator
The calculator is mentioned as a primary tool for performing calculations related to normal distribution, particularly for finding areas under the curve which correspond to probabilities. The video script suggests that while some calculations can be done by hand, the use of a calculator is more efficient and recommended for dealing with normal distribution problems.
💡Empirical Rule
The empirical rule is a statistical concept that provides a way to approximate probabilities for a normal distribution. It is associated with the percentages 68, 95, and 99.7, which represent the proportion of data within one, two, and three standard deviations from the mean, respectively. The video script uses the empirical rule to illustrate the distribution of data in a normal distribution.
💡Z-Score
A z-score is a measure of how many standard deviations an element is from the mean. In the video, z-scores are used to standardize scores and compare them to the mean within the context of a normal distribution. The script explains how to calculate z-scores and emphasizes their importance in understanding relative standing in a dataset.
💡Standard Normal Distribution
A standard normal distribution is a specific type of normal distribution where the mean (mu) is zero and the standard deviation (sigma) is one. The video script discusses the standard normal distribution as a basis for calculating z-scores and interpreting probabilities associated with different z-scores.
💡Cumulative Distribution Function (CDF)
The cumulative distribution function, or CDF, is a concept used to describe the probability that a random variable takes a value less than or equal to a certain value. In the video, the CDF is used in conjunction with the normal distribution to find probabilities associated with z-scores, as demonstrated by the normalcdf function on the calculator.
💡Continuous Random Variable
A continuous random variable is a variable that can take on any value within an interval, as opposed to discrete variables which can only take on specific values. The video script discusses how a continuous random variable with a symmetric, bell-shaped distribution can be described by the normal distribution formula.
💡Symmetric
Symmetry in the context of the video refers to the property of a normal distribution graph where the left and right sides of the curve are mirror images of each other. This characteristic is important for understanding the shape of the distribution and how data is distributed around the mean.
💡Mean
The mean, often denoted by the Greek letter mu (μ), is the average value of a dataset. In the video, the mean is central to the concept of z-scores and the standard normal distribution, where the mean is set to zero for standardization purposes.
💡Standard Deviation
Standard deviation is a measure of the amount of variation or dispersion in a set of values. In the video, it is used in the context of the normal distribution and z-scores, where it helps to understand how spread out the data is from the mean. The standard deviation is set to one in the standard normal distribution.
💡Area Under the Curve
The area under the curve in a normal distribution graph represents the probability of the random variable falling within a certain range. The video script explains that the total area under the curve is one, which corresponds to 100%, and is used to calculate probabilities for different ranges of the distribution.
Highlights

Introduction to the first video from chapter six with an expected duration of 20-30 minutes.

Announcement of future course structure with Zoom videos and set office hours for discussion.

Emphasis on the importance of the normal distribution formula and its characteristics such as symmetry and bell shape.

Explanation of the attributes of a normal distribution including single peak, bell-shaped curve, and total area under the curve equals one.

Clarification that the area under the normal density curve represents probabilities.

Brief mention of the uniform distribution and its equal probability across all values.

Discussion on the importance of the density curve in describing the pattern of a continuous distribution.

Introduction of the empirical rule and its use in approximating probabilities of a normal distribution.

Definition of the standard normal distribution with mean (mu) equal to zero and standard deviation (sigma) equal to one.

Explanation of the z-score as a measure of relative standing in comparison to the mean.

Focus on the use of calculators for normal distribution calculations rather than manual computation.

Instruction on using the normalcdf function on calculators for finding probabilities associated with z-scores.

Demonstration of how to calculate the probability of a z-score being less than a specific value using the calculator.

Illustration of calculating the probability of a z-score being greater than a specific value.

Method for finding the probability of a z-score falling between two given values.

Encouragement for students to practice using calculators to solve problems from the upcoming homework.

Closing remarks with an invitation for students to get comfortable with the Zoom platform and look forward to further discussions on Monday.

Transcripts

Browse More Related Video

Math 119 Chap 6 part 2

Elementary Statistics - Chapter 6 Normal Probability Distributions Part 1

Probabilities in a Normal Distribution - TI-84

Elementary Stats Lesson #11

Stats: Finding Probability Using a Normal Distribution Table

Standard Normal Distribution Tables, Z Scores, Probability & Empirical Rule - Stats

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
StatisticsNormal DistributionZ-ScoreEducationalOnline CourseEmpirical RuleCalculusGraphingProbabilityLearning ToolsStatistical Analysis