Math 119 Chap 6 part 2
TLDRThe video script is a detailed instructional session on understanding and solving probability problems involving z-scores and normal distribution. The instructor demonstrates how to use the inverse norm function on a calculator to find z-scores corresponding to given probabilities, and vice versa. The session covers various scenarios, including finding the probability of a z-score being less than a certain value, greater than a value, and between two values. It also applies these concepts to real-world examples, such as SAT scores and IQ distributions, emphasizing the importance of understanding the normal distribution and the use of technology to simplify calculations.
Takeaways
- 📚 The instructor is reviewing probability problems related to z-scores from a previous class.
- 🔍 The main difference between the problems discussed is that one asks for the z-score given a probability, while the other asks for the z-score that corresponds to a given probability.
- 📈 The instructor emphasizes the importance of visualizing the problem by drawing the normal distribution curve to understand the area under the curve that corresponds to the given probability.
- 🧮 The use of the calculator's inverse norm function is demonstrated to find z-scores that correspond to specific probabilities, such as finding a z-score for an area of 0.25 under the curve.
- ⚠️ The instructor clarifies that the z-score found is not a probability but a value on the standard normal distribution that corresponds to the given area.
- 📉 For problems involving 'greater than' probabilities, the instructor explains the need to find the z-score that has the specified area to its right due to the symmetrical nature of the normal distribution.
- 🤔 The concept of 'between a and b' probabilities is introduced, where the instructor shows how to find z-scores that correspond to the middle area of the distribution, using the calculator's inverse norm function with adjusted probabilities.
- 📝 The script includes practical examples, such as the probability of high school seniors qualifying for Division II sports based on SAT scores, demonstrating the application of normal distribution in real-world scenarios.
- 📉 The instructor explains how to use the normalcdf function on a calculator to find the probability of a score falling within a certain range, given the mean and standard deviation of the distribution.
- 🔢 The importance of converting non-standard normal distributions to z-scores for problems that do not directly provide them is highlighted, showing the process of standardization.
- 💡 The script concludes with a discussion on the distribution of IQ scores, emphasizing that they are normally distributed with a mean of 100 and a standard deviation of 15, and how to calculate the percentage of people with IQ scores within a specific range.
Q & A
What is the main topic discussed in the video script?
-The main topic discussed in the video script is the use of z-scores and the normal distribution in solving probability problems, including how to interpret and apply them using a calculator.
What is the difference between the problems discussed in the script?
-The difference between the problems is that in one, the z-score is given and the probability is sought, while in the other, the probability is given and the z-score is to be found.
What is the significance of drawing the normal distribution curve when solving these problems?
-Drawing the normal distribution curve helps visualize the problem, understand the area under the curve that corresponds to the given probability, and aids in comprehending what is being asked without just relying on the calculator.
How does the script describe the process of finding the z-score corresponding to a probability of 0.25?
-The script describes using the inverse norm function on a calculator, inputting an area of 0.25 with a mean of 0 and a standard deviation of 1, to find the z-score that corresponds to this area under the curve.
What is the z-score found for a probability of 0.25 according to the script?
-The z-score found for a probability of 0.25 is approximately -0.674, which is obtained using the inverse norm function on a calculator.
How does the script handle the problem of finding the z-score for a probability of 0.13 in the 'greater than' scenario?
-The script uses the inverse norm function with an input of 0.13 to find the z-score that has 0.13 area to the left. Since the calculator always calculates from left to right, the positive equivalent of the found negative z-score is used because the problem asks for 'greater than' the z-score.
What is the concept of symmetry in the normal distribution as discussed in the script?
-The concept of symmetry in the normal distribution as discussed in the script means that for every negative z-score, there is an equal and opposite positive z-score that corresponds to the same tail area in the distribution.
How does the script explain the process of finding the probability that a z-score is between two values?
-The script explains that to find the probability that a z-score is between two values, one should subtract the total probability (1) by the sum of the probabilities in the tails (outside the range), and then divide the result by two to find the probability in each tail, which are then symmetrical around the mean.
What is the significance of the 'inverse norm' function in the calculator as mentioned in the script?
-The 'inverse norm' function in the calculator is significant as it allows the user to input an area (probability) and find the corresponding z-score for that area under the standard normal distribution curve.
How does the script relate the concept of z-scores to real-world scenarios like SAT scores and water taxi loads?
-The script relates the concept of z-scores to real-world scenarios by demonstrating how to calculate the probability of certain outcomes, such as the percentage of high school seniors qualifying for Division II sports based on their SAT scores, or the probability of an adult man weighing less than a certain amount, using the normal distribution of the respective data.
Outlines
📚 Understanding Z-Scores and Probabilities
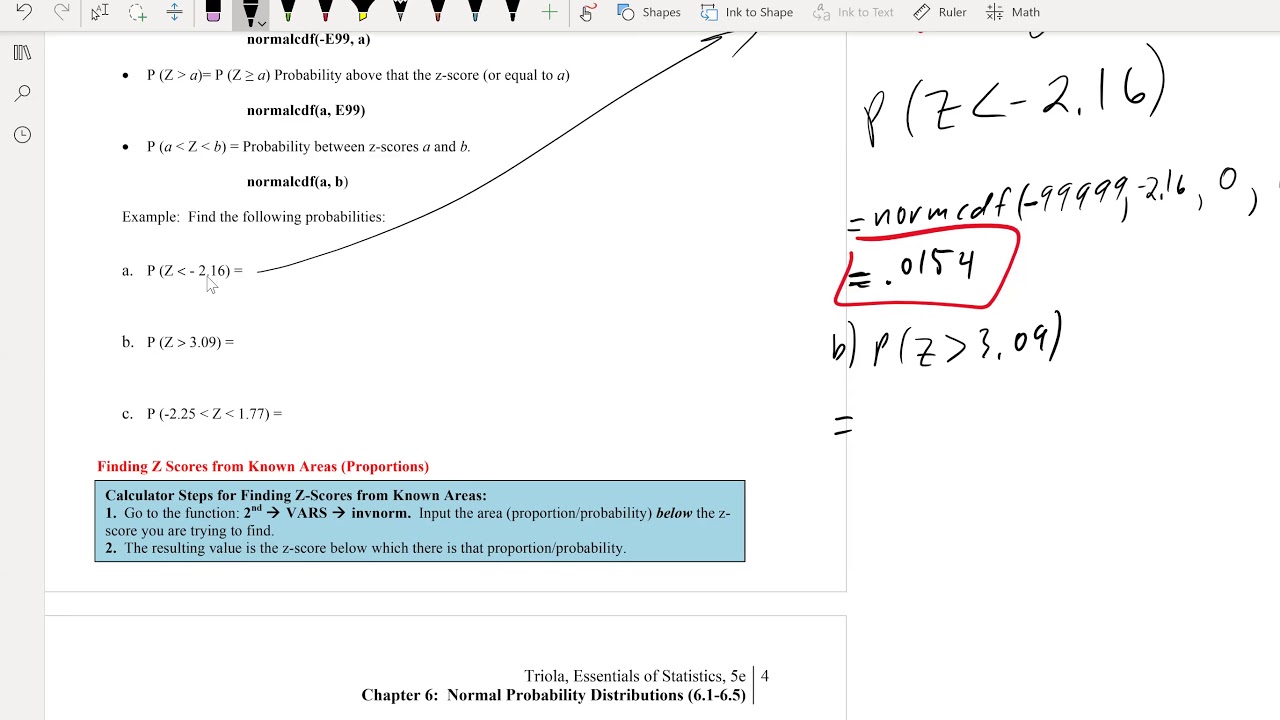
The instructor begins by revisiting problems from a previous class, focusing on the concept of Z-scores and their relation to probabilities. The main task is to interpret how given probabilities relate to Z-scores in standard normal distribution. The explanation walks through the process of finding a Z-score when the area under the normal curve to the left of the Z-score is known, using the inverse norm function on a calculator. The example given finds a Z-score corresponding to an area of 0.25, resulting in a Z-score of approximately -0.674. The instructor emphasizes the importance of visualizing the problem with a graph to enhance understanding.
📉 Probabilities of Greater Than and Less Than Z-Scores
This paragraph delves into the nuances of calculating probabilities for Z-scores that are greater than or less than a certain value. The instructor clarifies the difference between finding the Z-score for a given probability and vice versa. An example is provided where the probability of a Z-score being greater than a certain value is given, and the task is to find the Z-score. The use of the calculator's inverse norm function is demonstrated, and the importance of considering the symmetry of the normal distribution is highlighted. The summary also touches on the correct interpretation of 'greater than' and 'less than' in the context of Z-scores and probabilities.
📈 Working with Non-Standard Normal Distributions
The script moves on to problems involving non-standard normal distributions, where the mean and standard deviation are not the typical 0 and 1, respectively. The instructor outlines the steps to standardize observations to Z-scores and to find the probability of a proportion using the normal cumulative distribution function (CDF). An example is given involving the SAT scores of high school seniors, where the mean and standard deviation are provided, and the task is to find the percentage of students who qualify for Division II sports based on their SAT scores. The use of the normalcdf function on a calculator is demonstrated, and the process of converting raw scores to Z-scores for analysis is explained.
🔢 Applying Normal Distribution to Real-World Scenarios
The instructor applies the concepts of normal distribution to real-world scenarios, such as the weight distribution of adult men and the SAT scores of high school seniors. The focus is on using the normalcdf function to find probabilities for specific ranges of values. An example is given where the probability of a randomly selected man weighing less than 140 pounds is calculated, using the mean and standard deviation of the weight distribution of adult men. The process involves converting the raw weight value to a Z-score and then using the calculator to find the probability, resulting in approximately a 13% chance.
🧠 IQ Scores and Normal Distribution Application
The script concludes with an example of IQ scores, which are normally distributed with a mean of 100 and a standard deviation of 15. The task is to determine the percentage of people who have IQ scores between 85 and 120. The instructor demonstrates how to use the normalcdf function on a calculator to find the probability of an IQ score falling within this range, resulting in approximately 79.36%. The summary underscores the importance of understanding the parameters of a normal distribution and the ability to apply them to calculate probabilities for different score ranges.
Mindmap
Keywords
💡Probability
💡Z-score
💡Inverse Norm
💡Standard Deviation
💡Normal Distribution
💡Cumulative Distribution Function (CDF)
💡SAT Scores
💡Graphing Calculator
💡Standard Normal
💡IQ Scores
Highlights
Introduction to solving probability problems using z-scores and the normal distribution.
Explanation of the difference between finding the z-score given a probability and vice versa.
Demonstration of how to use the inverse norm function on a calculator to find z-scores.
Clarification on the importance of drawing the normal distribution curve to visualize the problem.
Illustration of calculating the z-score corresponding to a probability of 0.25.
Discussion on the symmetry of the normal distribution and its implications for z-scores.
Method to find the z-score for a probability of 'greater than' a certain value using the inverse norm function.
The concept of standardizing observations to z-scores for non-standard normal distributions.
Application of normalcdf function to find the percentage of high school seniors qualifying for Division II sports.
Use of the normal distribution to calculate the proportion of SAT scores falling between specific ranges.
Conversion of non-standard normal problems into z-scores for calculation using standard normal distribution methods.
Comparison between using calculator functions and manual standardization for normal distribution problems.
Example of calculating the probability of an adult man weighing less than 140 pounds based on a normal distribution of weights.
Importance of understanding the mean and standard deviation in the context of normal distribution.
Instruction on writing the correct distribution for IQ scores given a mean and standard deviation.
Calculation of the percentage of people with IQ scores between 85 and 120 using the normalcdf function.
Conclusion of the video with a summary of the methods and concepts covered for solving normal distribution problems.
Transcripts
Browse More Related Video
Math 119 Chap 6 part 1
Stats: Finding Probability Using a Normal Distribution Table

Elementary Stats Lesson #11

6.1.4 The Standard Normal Distribution - Given a range of z scores, find areas or probabilities.
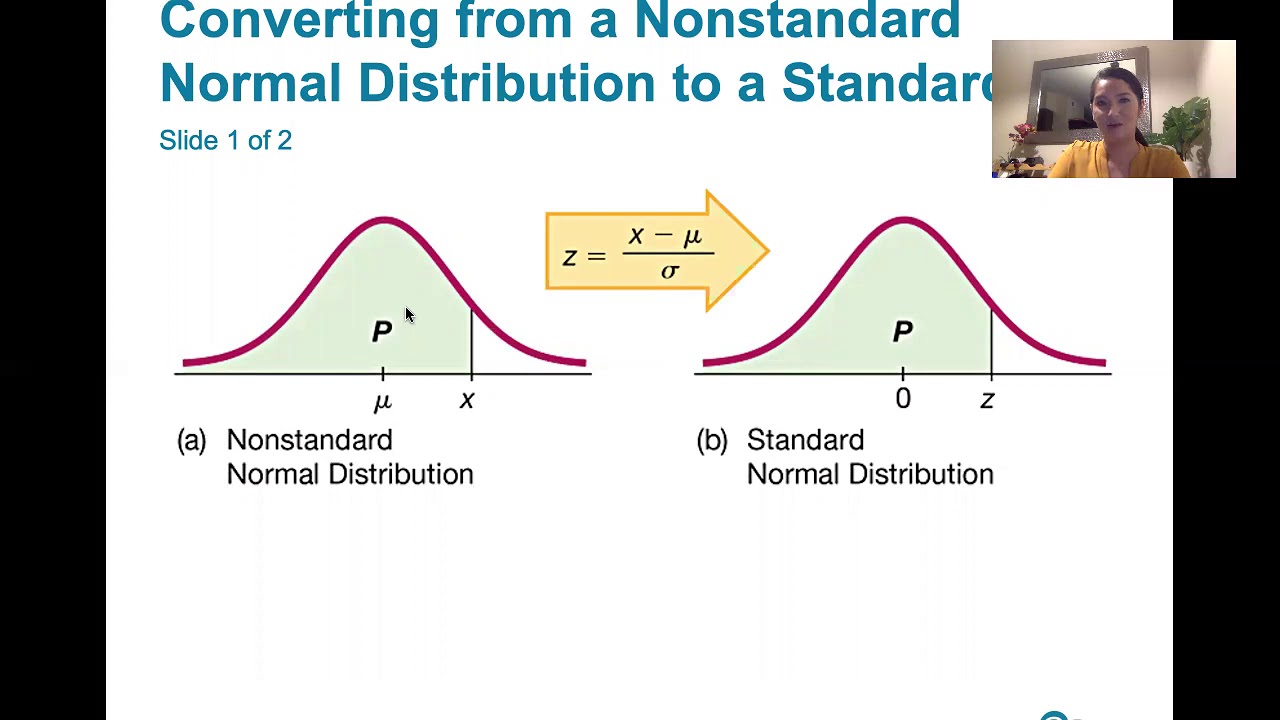
6.2.1 Nonstandard Normal Distributions -Converting B/t Standard and Nonstandard Normal Distributions

Find the z-score given the confidence level
5.0 / 5 (0 votes)
Thanks for rating: