Formulas for Trigonometric Functions: Sum/Difference, Double/Half-Angle, Prod-to-Sum/Sum-to-Prod

Professor Dave Explains
24 Jan 201809:28
EducationalLearning
32 Likes 10 Comments

TLDRThe video introduces important trigonometric formulas including the sum and difference formulas for sine, cosine, and tangent, which allow finding trig values for sums and differences of angles. It covers double-angle and half-angle formulas for simplifying or expanding trig functions. Power-reducing formulas express trig functions squared in terms of simpler trig functions. Product-to-sum and sum-to-product formulas transform products into sums and vice versa. Examples demonstrate applying the formulas to find exact trig values.

Takeaways
  • 😀 The sum and difference formulas allow us to evaluate sine and cosine for angles that are sums or differences of other angles.
  • 😇 There are double angle formulas that let us find sine, cosine, and tangent for twice a given angle.
  • 🤓 Power-reducing formulas express sine squared and cosine squared in terms of sine or cosine.
  • 😎 Half-angle formulas give sine, cosine, and tangent for half a given angle in terms of that angle.
  • 🧐 Product-to-sum formulas turn products of trig functions into sums and differences.
  • 🤔 Sum-to-product formulas turn sums and differences of trig functions into products.
  • 👍 The sum and difference tangent formulas allow us to find tangent for sums and differences.
  • 😊 Derivations for the formulas can be complex, so we focused on application.
  • 🙂 Exact trig values can be more useful than approximations.
  • 😉 These formulas have applications in areas like calculus and identity verification.
Q & A

  • What are the sum and difference formulas for sine and cosine?

    -The sum and difference formulas for sine and cosine allow you to find the sine or cosine of an angle that is the sum or difference of two other angles in terms of the sines and cosines of those two angles.

  • How can you use the sum and difference formulas to find trig values not on the unit circle?

    -You can split up the desired angle into two component angles that are on the unit circle. Then plug those values into the appropriate sum or difference formula to find the trig value for the original angle.

  • What are the double angle formulas for sine, cosine, and tangent?

    -The double angle formulas are: Sine(2θ) = 2*sin(θ)*cos(θ) Cosine(2θ) = cos^2(θ) - sin^2(θ) Tangent(2θ) = 2*tan(θ)/(1 - tan^2(θ))

  • What are the power-reducing formulas?

    -The power-reducing formulas express sine squared, cosine squared, and tangent squared in terms of sine, cosine, and tangent respectively. They allow you to reduce the power of the trig function.

  • What are the half-angle formulas and how are they useful?

    -The half-angle formulas express sine, cosine, and tangent of an angle in terms of the cosine of twice that angle. They allow you to find trig values for smaller angles based on larger angles with known values.

  • What are the product-to-sum formulas?

    -The product-to-sum formulas express the product of two trig functions involving different angles as the sum or difference of trig functions involving the sum and difference of those angles.

  • What are the sum-to-product formulas?

    -The sum-to-product formulas express the sum or difference of two trig functions as a product of trig functions.

  • How can you use the product-to-sum formulas?

    -You can use the product-to-sum formulas to transform products of trig functions into sums or differences, which can be useful for verifying trig identities.

  • Why are the sum and difference formulas important to know?

    -The sum and difference formulas allow you to find exact trig values for angles not on the unit circle by breaking them into component angles you can evaluate. This avoids approximation errors.

  • What are some key uses for the double angle and half angle formulas?

    -The double angle formulas allow you to find trig values for twice an angle based on the original angle. The half angle formulas do the opposite - finding values for half an angle from the full angle.

Outlines
00:00
📐 Understanding Trigonometric Formulas

This section introduces essential trigonometric formulas, focusing on sum and difference formulas for sine and cosine, double-angle formulas, and power-reducing formulas. It demonstrates how to apply these formulas to calculate exact values for trigonometric functions of specific angles, such as cosine of five twelfths pi, by breaking them down into more manageable angles. The segment emphasizes the practicality of these formulas in finding exact values without resorting to approximations and sets the stage for further exploration of trigonometric identities, including the derivation of double-angle and power-reducing formulas.

05:05
🔍 Expanding Trigonometry: Half-Angle and Product-to-Sum Formulas

This paragraph delves into more advanced trigonometric concepts, introducing half-angle formulas and product-to-sum, as well as sum-to-product formulas. It explains how half-angle formulas can evaluate trig functions for smaller angles based on known values for larger angles, using square roots and considering the quadrant to determine the sign. The discussion extends to product-to-sum and sum-to-product formulas, illustrating how they express trigonometric functions involving two angles as products or sums. These formulas are presented as useful tools for solving complex problems and verifying identities, though they are acknowledged as challenging to memorize.

Mindmap
Keywords
💡trig functions
Trigonometric functions like sine, cosine, and tangent that relate the angles and sides of a right triangle. They are used throughout mathematics and physics. The video introduces important formulas for evaluating trig functions.
💡sum and difference formulas
Allow you to evaluate the sine or cosine for an angle equal to the sum or difference of two other angles. This is useful because many angles are not on the unit circle.
💡double-angle formulas
Allow you to evaluate trig functions for twice a given angle based on the trig functions of the original angle. For example, cosine of 2x can be written in terms of cosine and sine of x.
💡power-reducing formulas
Express the square of a trig function for an angle in terms of the non-squared trig function. For example, sine squared x can be written in terms of just cosine x.
💡half-angle formulas
Allow you to evaluate trig functions for half a given angle based on the trig functions of the original angle. Useful when the smaller angle is not on the unit circle.
💡product-to-sum formulas
Express the product of two trig functions of different angles as a sum of trig functions of combined angles. For example, sine x cosine y becomes sine(x+y) + sine(x-y).
💡sum-to-product formulas
Reverse of product-to-sum, expressing the sum of two trig functions as a product of trig functions.
💡identities
Equalities between trig expressions that are always true. The video shows how product-sum, sum-product, and other formulas can help verify trig identities.
💡unit circle
The circle of radius 1 centered at the origin on which exact trig function values can be defined. Memorizing these is essential for using other formulas.
💡quadrant
Each of the 4 regions divided by the x and y axes on the coordinate plane. Quadrant dictates sign of trig functions so must consider when using half-angle and other formulas .
Highlights

First significant research finding

Introduction of new theoretical model

Description of innovative experimental method

Transcripts

Browse More Related Video

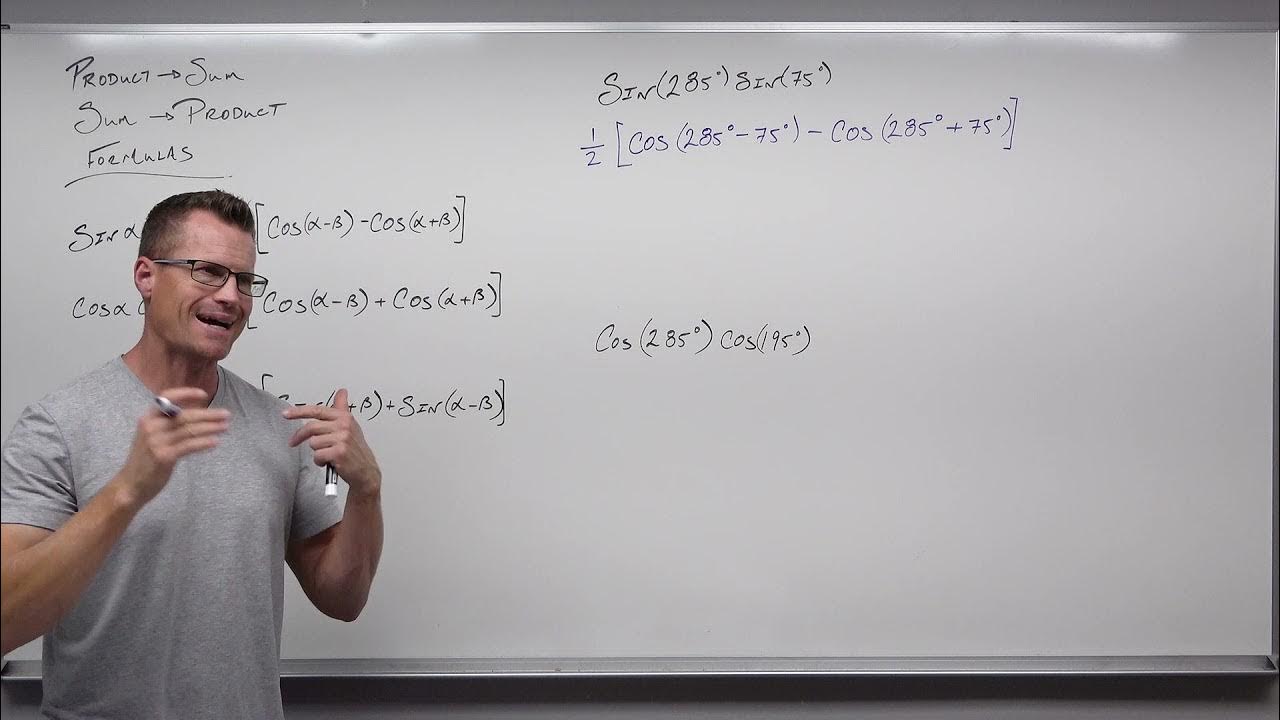
How to Use Product to Sum and Sum to Product Formulas in Trig (Precalculus - Trigonometry 29)

Precalc 5.4 Sum and Difference Formulas

Sum and Difference Identities of Sine and Cosine

Product To Sum Identities and Sum To Product Formulas - Trigonometry

5.5 Multiple Angle and Product to Sum Formulas (Part 1)

Trig Identities

Rate This

5.0 / 5 (0 votes)

Thanks for rating: