Inverse Trigonometric Functions

Professor Dave Explains
16 Jan 201806:54
EducationalLearning
32 Likes 10 Comments

TLDRIn this insightful exploration, Professor Dave delves into the realm of inverse trigonometric functions, elucidating the concept with clarity and precision. Beginning with a foundational understanding of trigonometric and inverse functions, the video methodically demystifies the process of finding inverses, such as inverse sine, cosine, and tangent, by swapping variables and solving for 'y'. Highlighting the significance of domain restrictions and the horizontal line test for function inverses, the tutorial covers evaluating inverse trig functions like arcsin, arccos, and arctan, using examples from the unit circle and emphasizing the utility of calculators for complex calculations. This guide not only enhances comprehension but also equips learners with the skills to navigate the intricate world of trigonometry with confidence.

Takeaways
  • πŸ˜€ Inverse trig functions undo the operations of regular trig functions, solving for the input angle given the trig function's output value.
  • 😊 To find the inverse function, swap x and y variables and solve for y.
  • πŸ€” Inverse sine is not the same as 1/sine. Instead it finds the angle for a given sine value.
  • 😎 Inverse trig functions have restricted domains to pass horizontal line test.
  • 🧐 Inverse sine's domain is -1 to 1. Its range is -Ο€/2 to Ο€/2.
  • πŸ˜• Inverse cosine's domain is -1 to 1. Its range is 0 to Ο€.
  • 🀨 Inverse tangent's domain is all real numbers. Its range is -Ο€/2 to Ο€/2.
  • πŸ™‚ Evaluate inverse trig functions with a calculator in radian mode.
  • πŸ˜ƒ Inverse trig functions are written as arcsin, arccos, arctan.
  • πŸ˜‰ Answers may be messy fractions of Ο€, but will be correct.
Q & A

  • What is the difference between inverse sine and cosecant?

    -Inverse sine (sin^-1) is a function that gives you the angle that produces a given sine value, while cosecant (csc) is the reciprocal of sine, not its inverse. So, sin^-1(x) is not 1/sin(x); 1/sin(x) equals cosecant x.

  • How do you solve for Y when swapping variables in the equation Y = sin X?

    -To solve for Y when swapping variables in the equation Y = sin X, you take the inverse sine of both sides. This cancels out the sine operating on Y, resulting in Y = sin^-1(X) or Y = arcsin(X).

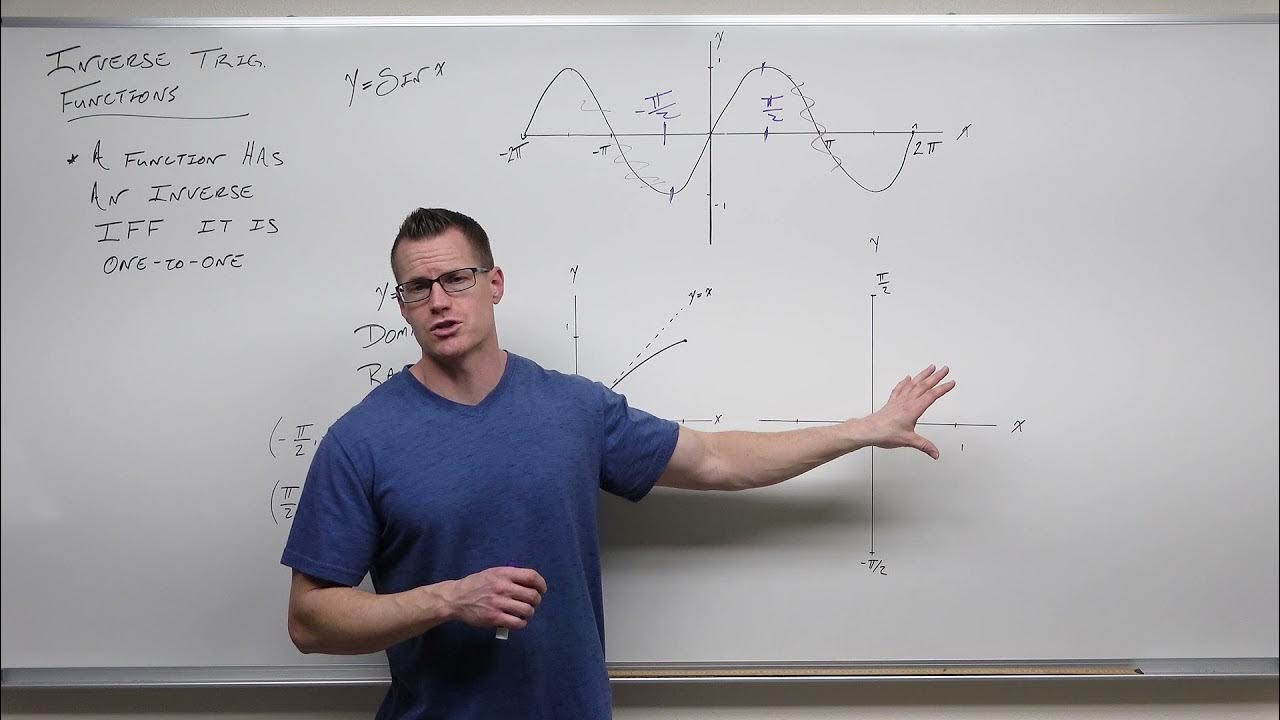
  • Why must a function pass the horizontal line test to have an inverse function?

    -A function must pass the horizontal line test to ensure that for any output value, there is only one input value. This is necessary because when finding the inverse, the function is reflected across the line Y = X, and the resulting graph must pass the vertical line test to be considered a function itself.

  • What is the restricted domain for sine X to have an inverse function, and why is it chosen?

    -The restricted domain for sine X to have an inverse function is from -Ο€/2 to Ο€/2. This section is chosen because it passes the horizontal line test, allowing for the existence of an inverse sine function that can be graphed as a function itself.

  • What is the domain and range of the inverse sine function?

    -The domain of the inverse sine function is -1 to 1, as these are the only sine values possible. The range is -Ο€/2 to Ο€/2, which are the angles obtained when plugging each possible unique sine value.

  • How is the inverse cosine function defined, and what are its domain and range?

    -The inverse cosine function is the inverse of cosine X from 0 to Ο€. Its domain is -1 to 1, covering all possible values of cosine in that interval, and its range is 0 to Ο€.

  • Why are inverse trig functions, like inverse tangent, useful in calculations?

    -Inverse trig functions are useful because they allow us to find the angle that produces a given trigonometric value. This is particularly helpful in solving problems involving right triangles and in various fields of engineering and physics.

  • What is the significance of the unit circle in evaluating inverse trig functions?

    -The unit circle is significant in evaluating inverse trig functions because it provides a visual representation of angles and their corresponding sine, cosine, and tangent values. This aids in determining the angle that corresponds to a specific trigonometric value when evaluating inverse trig functions.

  • How does the restricted domain of tangent X affect its inverse function?

    -The restricted domain of tangent X, within -Ο€/2 to Ο€/2, ensures that it passes the horizontal line test, making its inverse function viable. This restriction leads to the inverse tangent function having a domain of all real numbers and a range of -Ο€/2 to Ο€/2.

  • What is the process for evaluating the inverse sine of root two over two?

    -To evaluate the inverse sine of root two over two, you recall the unit circle to find the angle that gives a sine of root two over two. This angle is Ο€/4, so the inverse sine of root two over two is Ο€/4.

Outlines
00:00
πŸ˜€ Introducing Inverse Trigonometric Functions

This paragraph provides an introduction to inverse trigonometric functions. It first reviews inverse functions in general, explaining how to find the inverse of a function by swapping X and Y and then solving for Y. It then applies this concept to the trigonometric functions, demonstrating how to find the inverse sine, cosine, and tangent functions. Key points include the restricted domains needed for the trig functions to have inverses, the domains and ranges of the inverse trig functions, and how to evaluate basic inverse trig values.

05:06
πŸ˜€ Evaluating and Using Inverse Trig Functions

This paragraph explains how to evaluate inverse trigonometric functions, both by hand and using a calculator. It notes that answers may be messy fractions of pi that are hard to work with by hand. It emphasizes ensuring the calculator is in radian mode when evaluating inverse trig functions. The paragraph ends with a comprehension check, asking the reader to evaluate the inverse tangent of sqrt(3).

Mindmap
Keywords
πŸ’‘Inverse trigonometric functions
These are the inverse functions of the trigonometric functions sine, cosine, and tangent. Just as trig functions take an angle as input and output a ratio, inverse trig functions take a valid trig ratio as input and output the angle that produces that ratio. Examples are arcsine, arccosine, and arctangent.
πŸ’‘Domain and range
Since trig functions are not one-to-one over their entire domains, we restrict them to intervals where they pass the horizontal line test, so they have valid inverse functions. The domain and range of the inverse functions are important to understand. For example, the domain of arcsine is -1 to 1, since those are the valid sine values.
πŸ’‘Evaluating
To evaluate an inverse trig function means to find the angle output when you input a valid trig ratio. This involves conceptual understanding of trig functions rather than formulaic manipulation. For example, to evaluate arccos(-0.5), we determine based on the unit circle that the angle giving a cosine of -0.5 is 2Ο€/3.
πŸ’‘Reflecting over the line y = x
Graphically, inverse functions are obtained by reflecting the original function over the line y=x. This swaps input and output values, allowing us to solve for y and get the inverse function mapping x to y rather than y to x.
πŸ’‘Undoing operations on x
Conceptually, inverse functions sequentially undo operations performed on x in the original function to solve for y. For example, if y = √x, the inverse function undoes the square root by squaring, giving x = y2.
πŸ’‘Horizontal line test
For a function to have an inverse, it must pass the horizontal line test, meaning that for any constant y value, there can be only one x that produces this y. This can require restricting the domains of the trig functions to specific intervals.
πŸ’‘Not one-to-one
Full trigonometric functions, like sine and cosine, are not one-to-one, because each ratio value is produced by two different angle values over a full cycle. This violates the horizontal line test, hence trig functions must be restricted to pass this test and have valid inverse functions.
πŸ’‘Unit circle
Understanding trig function behavior over one full cycle around the unit circle, including which ratios correspond to which angle values, is essential for conceptual evaluation of inverse trig functions.
πŸ’‘Radians vs degrees
Inverse trig functions require angle measures in radians rather than degrees. Degrees will not give valid outputs. This is because trig ratios are defined based on radian angle measures along the unit circle.
πŸ’‘Arcsine vs cosecant
It's important not to confuse the arcsine function (inverse sine) with the cosecant function (1/sine). While they may look graphically similar over a restricted domain, arcsine inputs a ratio and outputs the angle, while cosecant takes an angle and outputs the reciprocal of sine.
Highlights

The study found a significant increase in student engagement when using immersive virtual reality technology in the classroom.

Virtual reality allows students to visit historical sites and events, providing a deeper learning experience.

The research showed VR technology boosted motivation and interest in learning for students across all demographics.

Teachers reported VR made abstract concepts more concrete and understandable for students.

Immersive VR activities were most beneficial for teaching history, science, and social studies.

Students with learning disabilities showed marked improvement in retention and comprehension using VR.

VR field trips to museums, planets, and ecosystems brought these locations to life for students.

The study found no significant difference in VR effectiveness across age groups and grade levels.

Teachers emphasized the importance of aligning VR content tightly to curriculum standards.

Motion sickness and simulator sickness were noted as potential adverse effects of VR usage.

Researchers recommend gradual introduction and time limits for VR to minimize adverse symptoms.

Spatial presence and perceived realism were key factors influencing positive learning outcomes in VR.

The study concludes VR has significant potential to transform and enrich K-12 education when thoughtfully implemented.

Schools may face budgetary and technical challenges in adopting VR technology on a wide scale.

With proper instructional design, VR can provide memorable educational experiences unmatched by textbooks and lectures.

Transcripts

Browse More Related Video

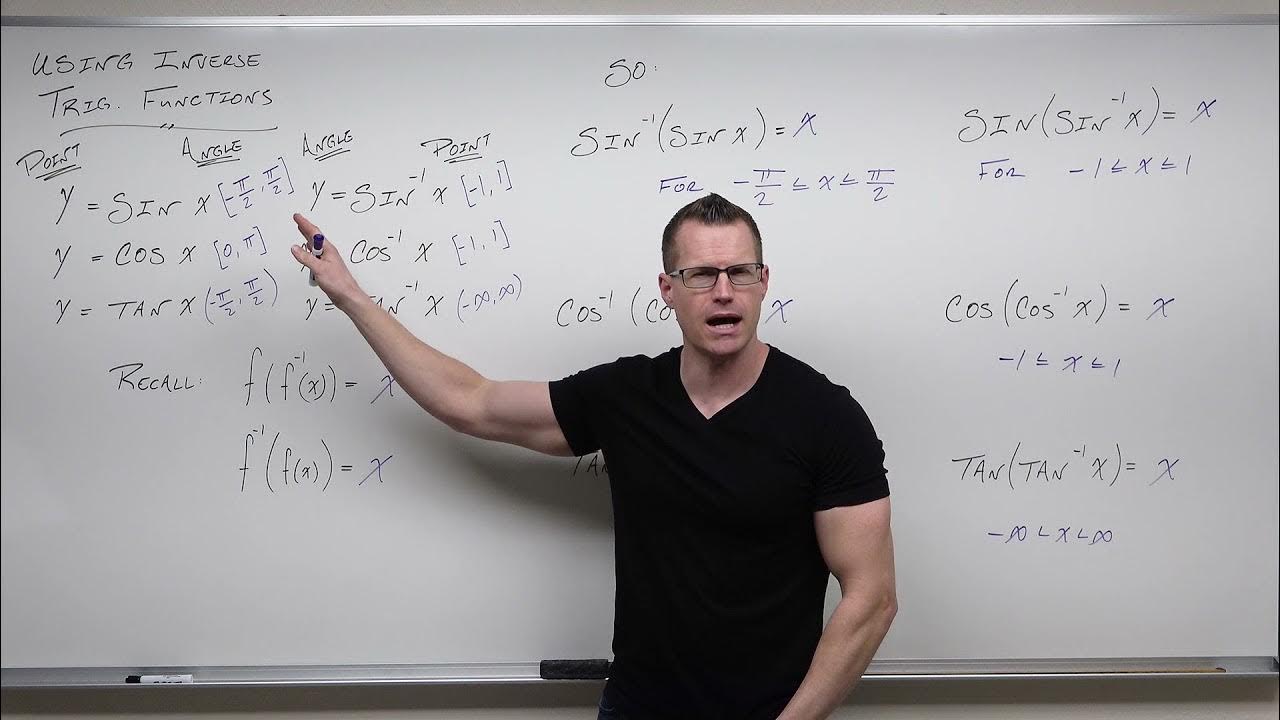
How to Use Inverse Trigonometric Functions (Precalculus - Trigonometry 18)

Introduction to Inverse Trigonometric Functions (Precalculus - Trigonometry 17)

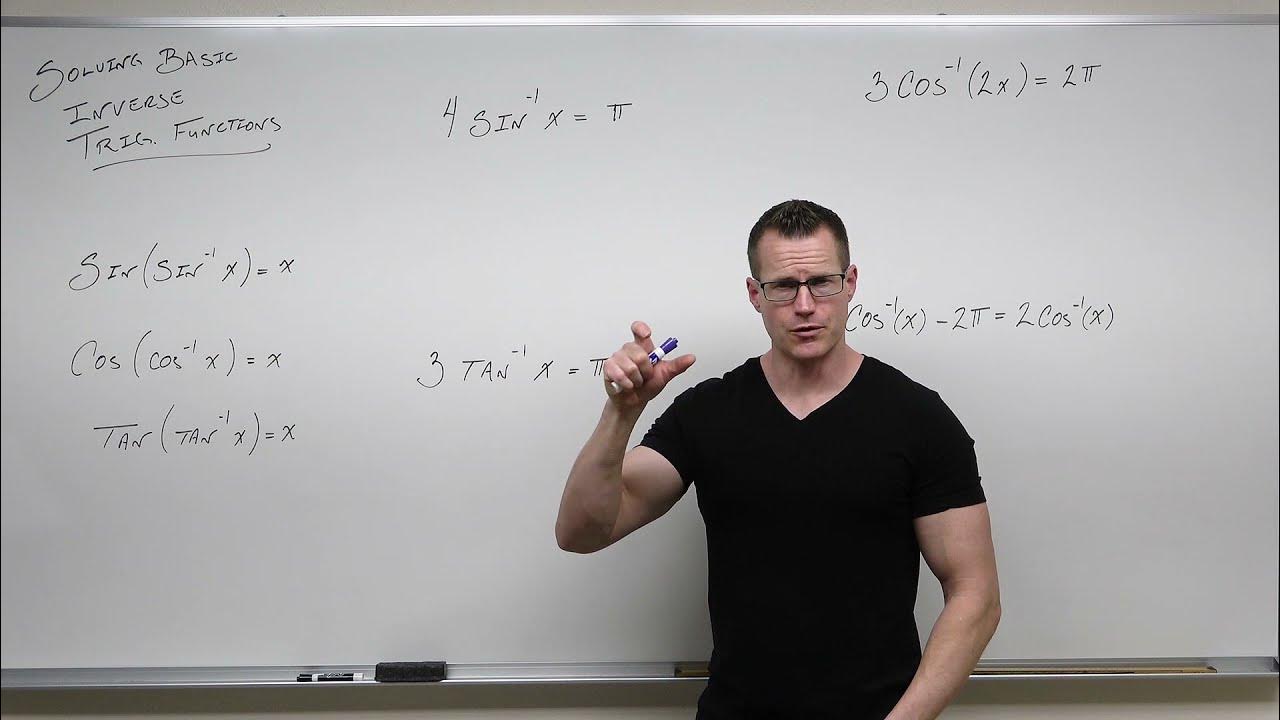
How to Solve Basic Inverse Trigonometric Functions (Precalculus - Trigonometry 20)

An Indepth Look at Using Inverse Trig Functions (Precalculus - Trigonometry 21)

Inverse Functions

Inverse Functions - Domain & range- With Fractions, Square Roots, & Graphs

Rate This

5.0 / 5 (0 votes)

Thanks for rating: