Introduction to Trigonometry: Angles and Radians
TLDRThis script introduces trigonometry, describing how to measure angles in radians on the coordinate plane. It explains that one radian is the angle subtended by an arc equal in length to the radius of a circle. There are 2π radians in a full circle, so π radians covers half a circle. Common angles like π/6 and π/4 radians are shown on a coordinate plane diagram. The video also covers converting between radians and degrees, and the concept of coterminal angles that differ by 2π. It ends by urging memorization of common trigonometric angles for easier comprehension going forward.
Takeaways
- 😀 Trigonometry deals with triangles, angles and new functions.
- 😊 Radians measure angles differently than degrees.
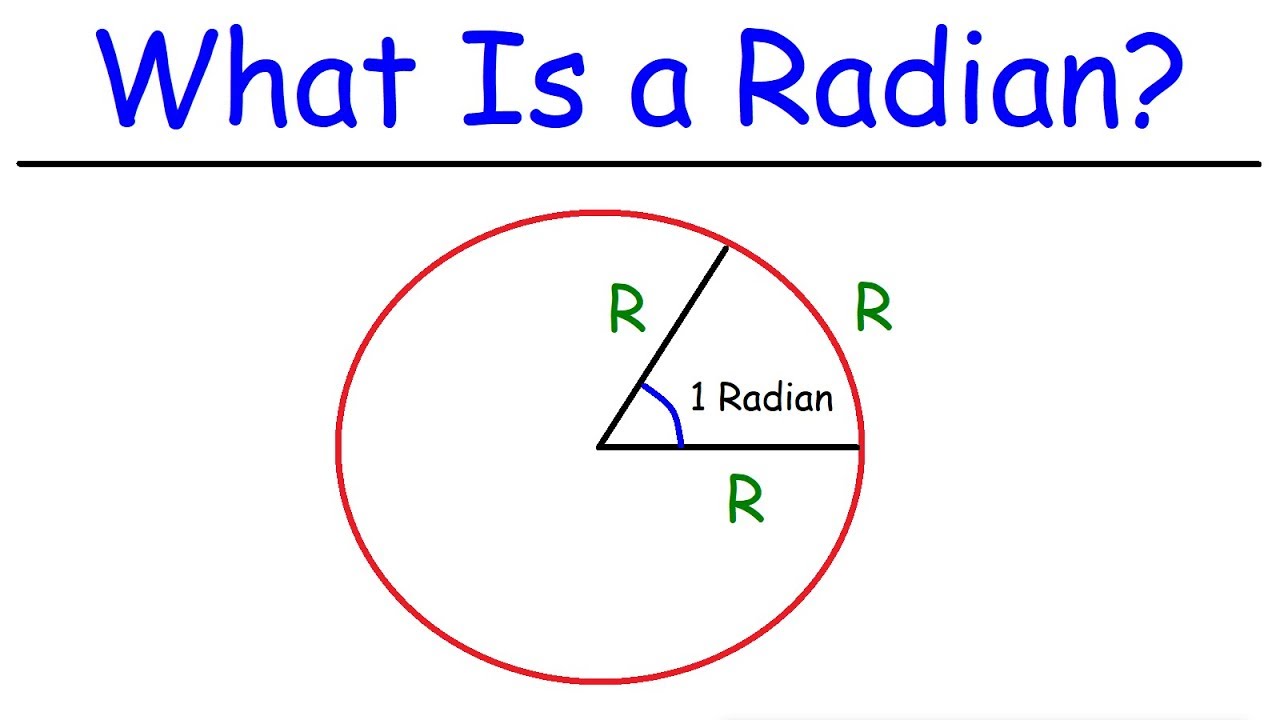
- 📐 A radian is the angle made when the arc length equals the radius.
- 🌡️ There are 2π radians in a full circle, equal to 360°.
- ➗ To convert between degrees and radians, divide by 180° and multiply by π.
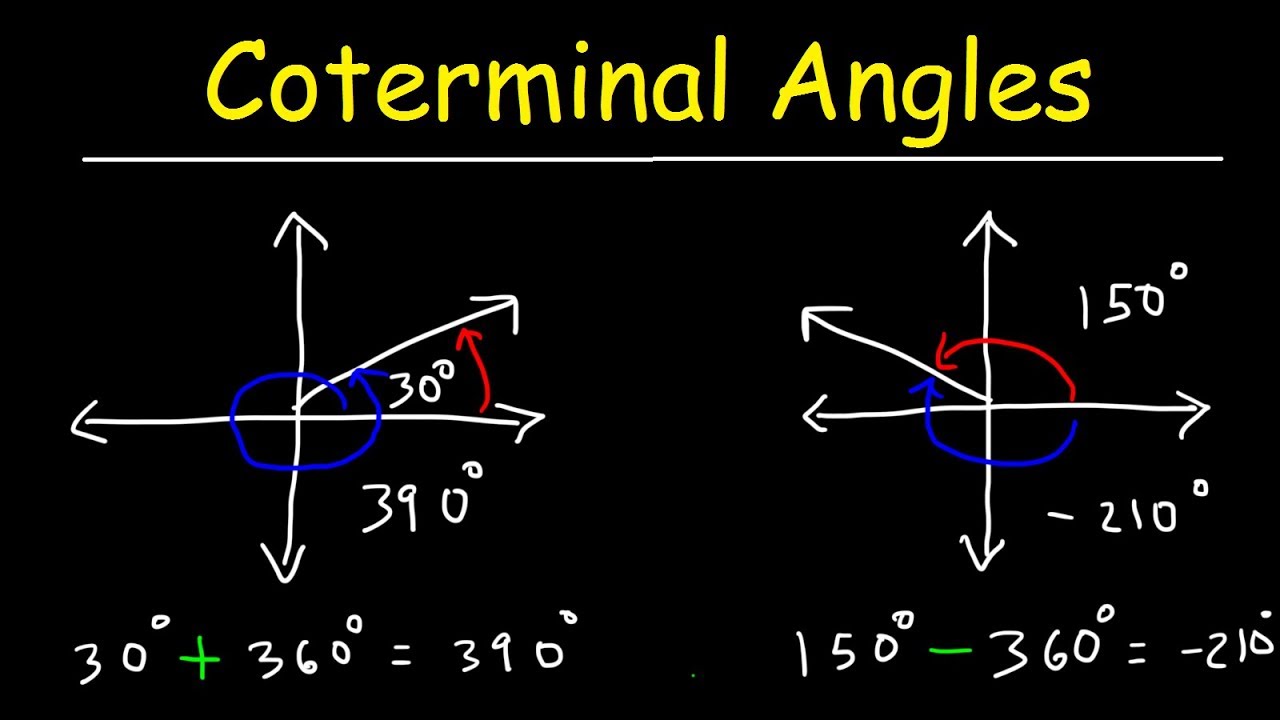
- 🤝 Coterminal angles end at the same spot and differ by multiples of 2π or 360°.
- 🧮 Common angles like 30°, 45° and 90° can be converted to π/6, π/4 and π/2 radians.
- 📈 New trig functions like sine, cosine and tangent are introduced.
- 💡 Understanding radians on the coordinate plane is key.
- 🧠 Memorizing common angles in radians will make trigonometry easier.
Q & A
What is trigonometry?
-Trigonometry is a branch of mathematics that deals with triangles, angles, and introduces new functions that describe relationships between angles and sides of triangles.
Why do we use radians to measure angles in trigonometry?
-Radians provide a direct relationship between the arc length of a circle and its radius, making calculations involving angles and the geometry of circles more intuitive and directly related to the circle's properties.
How is a radian defined?
-A radian is defined as the angle created when the arc length between two radii of a circle is equal to the radius of the circle.
What is the relationship between degrees and radians?
-360 degrees is equivalent to 2π radians. To convert between degrees and radians, you can divide by 180 and multiply by π for degrees to radians, or divide by π and multiply by 180 for radians to degrees.
How can you convert 30 degrees to radians?
-To convert 30 degrees to radians, divide 30 by 180 and multiply by π, resulting in π/6 radians.
What are coterminal angles?
-Coterminal angles are angles that share the same starting and ending points on a circle but may have different magnitudes, differing by multiples of 360 degrees or 2π radians.
Why are 360 degrees used to represent a full circle?
-The use of 360 degrees may originate from ancient Babylonians, who approximated a year as 360 days and used a base-60 counting system. The number 360 has many factors, making it versatile for calculations.
How do you convert two-thirds π radians to degrees?
-To convert two-thirds π radians to degrees, remove π and multiply by 180, resulting in 120 degrees.
What is the significance of understanding radians in trigonometry?
-Understanding radians is crucial in trigonometry because it allows for easier calculation of angles and arc lengths in circles, which is fundamental for studying and applying trigonometric functions.
Why is it recommended to memorize certain angles in both degrees and radians?
-Memorizing certain angles in both degrees and radians facilitates the understanding and application of trigonometric functions, making calculations quicker and easier, especially for commonly used angles.
Outlines
😀 Introducing Trigonometry and Radians
Paragraph 1 introduces trigonometry, stating it deals with triangles and angles. It explains that new functions will be introduced that may seem abstract at first but will make sense later. The concept of angles is reviewed using the coordinate plane. Radians are then introduced as an alternative to degrees for measuring angles, with 2π radians equaling 360 degrees.
😃 Memorizing Key Angles in Degrees and Radians
Paragraph 2 recommends memorizing common angles in both degrees and radians that are multiples of 30 degrees (π/6 radians) and 45 degrees (π/4 radians). It states that memorizing these values will make working with trigonometric functions much easier.
Mindmap
Keywords
💡trigonometry
💡angles
💡radians
💡coterminal angles
💡sine
💡cosine
💡tangent
💡coordinate plane
💡trigonometric functions
💡right triangle
Highlights
The research used an innovative combination of computational modeling and neuroimaging to understand decision making.
The findings provide new insight into the neural mechanisms underlying loss aversion bias in risky decision making.
The computational model accurately predicted behavior and identified a novel role for the ventral striatum in loss aversion.
Loss aversion was associated with increased connectivity between ventral striatum and ventromedial prefrontal cortex.
The work makes important theoretical contributions to prospect theory and the neuroscience of decision making under risk.
Understanding the neural basis of biases like loss aversion can inform efforts to improve decision making.
The combined modeling and neuroimaging approach could be applied to study other aspects of decision making.
The findings have practical implications for addressing biased risk-taking in domains like finance and health.
The computational model provides a tool to predict and modulate loss aversion bias in decision making.
This research significantly advances our understanding of the psychological and neural mechanisms of loss aversion.
Modulating loss aversion bias could help improve decision making in application areas like investing.
The ventral striatum may encode loss aversion by representing the negative utility of potential losses.
Loss aversion demonstrates the importance of emotions and affect in biased decision making.
This interdisciplinary approach combining modeling, behavior, and neuroimaging holds promise.
The findings open future research directions to causally probe the neural drivers of loss aversion.
Transcripts
Browse More Related Video

Radians and Degrees

CONVERTING DEGREE MEASURE TO RADIAN MEASURE AND VICE VERSA || PRE-CALCULUS
Coterminal Angles In Radians & Degrees - Basic Introduction, Trigonometry

Converting Radians and Degrees (Precalculus - Trigonometry 4)
Trigonometry - What Exactly Is a Radian?

Trig 0.1 - Angles, Degrees and Radians
5.0 / 5 (0 votes)
Thanks for rating: