Trigonometric Functions: Sine, Cosine, Tangent, Cosecant, Secant, and Cotangent

Professor Dave Explains
28 Dec 201707:18
EducationalLearning
32 Likes 10 Comments

TLDRThe video introduces trigonometric functions using right triangles constructed within a coordinate plane. After defining sine, cosine, and tangent using the side lengths of a triangle and its angles, the instructor introduces cosecant, secant, and cotangent as the reciprocals. Using two special right triangles, the values of the trig functions for 30°, 60°, and 45° angles are derived. The summary conveys the key essence of the script - explaining trigonometric functions geometrically and deriving some common examples - in clear yet engaging language.

Takeaways
  • 😀 Trigonometric functions relate the angles and side lengths of right triangles.
  • 😃 The sine, cosine, and tangent ratios compare the lengths of the sides.
  • 🤓 SOHCAHTOA helps remember sine = opp/hyp, cos = adj/hyp, tan = opp/adj.
  • 🧐 The reciprocals are cosecant, secant, and cotangent.
  • 😎 Special 30-60-90 and 45-45-90 triangles have useful sine/cosine values.
  • 👍 Radians measure angles by the arc length on a circle subtended by the angle.
  • 📐 Circles help visualize how trig functions change with the angle.
  • 📏 Legs of the triangle are called adjacent and opposite relative to the angle.
  • 🤯 Memorize exact trig values for 30°, 45°, 60° angles.
  • 🧮 Apply trig functions to calculate missing sides and angles in right triangles.
Q & A

  • What are the three main trigonometric functions?

    -The three main trigonometric functions are sine, cosine, and tangent.

  • How is sine defined?

    -Sine is defined as the ratio of the length of the side opposite to the angle in a right triangle to the length of the hypotenuse.

  • How is cosine defined?

    -Cosine is defined as the ratio of the length of the side adjacent to the angle in a right triangle to the length of the hypotenuse.

  • How is tangent defined?

    -Tangent is defined as the ratio of the length of the side opposite to the angle in a right triangle to the length of the side adjacent to the angle.

  • What are the three reciprocal trigonometric functions?

    -The three reciprocal trigonometric functions are cosecant, secant, and cotangent. Cosecant is the reciprocal of sine, secant is the reciprocal of cosine, and cotangent is the reciprocal of tangent.

  • What are the side lengths of a 30-60-90 triangle?

    -In a 30-60-90 triangle, if the shortest side has length 1, the next longest side has length √3, and the hypotenuse has length 2.

  • What are the trig values for a 30 degree angle in a 30-60-90 triangle?

    -In a 30-60-90 triangle, sin(30°) = 1/2, cos(30°) = √3/2, tan(30°) = √3/3.

  • What are the side lengths of a 45-45-90 triangle?

    -In a 45-45-90 triangle, if one leg has length 1, the other leg also has length 1, and the hypotenuse has length √2.

  • What are the trig values for a 45 degree angle in a 45-45-90 triangle?

    -In a 45-45-90 triangle, sin(45°) = cos(45°) = √2/2, and tan(45°) = 1.

  • What mnemonic can be used to remember the definitions of sine, cosine and tangent?

    -The mnemonic SOHCAHTOA can be used: Sine = Opposite/Hypotenuse, Cosine = Adjacent/Hypotenuse, Tangent = Opposite/Adjacent.

Outlines
00:00
📐 Introducing Trigonometric Functions

This paragraph introduces trigonometric functions and explains how to construct right triangles using the radius of a circle. It defines sine, cosine, and tangent as ratios between the lengths of the sides of a right triangle. The mnemonic SOHCAHTOA is provided to remember these definitions.

05:06
😎 Evaluating Trig Functions for Special Triangles

This paragraph calculates the sine, cosine, and tangent of the angles in 30-60-90 and 45-45-90 right triangles. The values are sine(30°)=1/2, cos(30°)=√3/2, tan(30°)=√3/3, sine(60°)=√3/2, cos(60°)=1/2, tan(60°)=√3, sine(45°)=√2/2, cos(45°)=√2/2, tan(45°)=1.

Mindmap
Keywords
💡Trigonometric Functions
Trigonometric functions are mathematical functions that relate the angles of a triangle to the ratios of its sides. In the video, these functions are introduced as essential tools for describing the relationships between the angles and side lengths in right triangles, as well as their extension to circular motion. Examples provided include sine, cosine, and tangent, which are fundamental in understanding the geometry of circles and triangles, highlighting their significance in both theoretical and practical aspects of trigonometry.
💡Radians
Radians are a unit of angular measure used in mathematics and physics to express angles. They are introduced in the video as a way to measure angles in a circle, offering a direct link between linear and angular measurements. Radians play a crucial role in trigonometry and the trigonometric functions, as they provide a natural way to describe angles in terms of the circle's radius, thus connecting the concept of circular motion with trigonometric relationships.
💡Coordinate Plane
The coordinate plane is a two-dimensional plane formed by the intersection of a vertical y-axis and a horizontal x-axis. In the video, the coordinate plane serves as the backdrop for illustrating how circles and right triangles relate to trigonometry. By drawing a circle and a radius in the coordinate plane, the video demonstrates the creation of right triangles, thereby visually explaining the geometric basis of trigonometric functions.
💡Hypotenuse
The hypotenuse is the longest side of a right triangle, opposite the right angle. It's emphasized in the video as the radius of the circle when a right triangle is formed by drawing a radius and a perpendicular line to the x-axis. The hypotenuse's constant length, regardless of the angle's size, illustrates the foundational role of the hypotenuse in defining the sine, cosine, and tangent functions.
💡SOHCAHTOA
SOHCAHTOA is a mnemonic device used to remember the definitions of the sine, cosine, and tangent trigonometric functions. The video employs SOHCAHTOA to make these definitions easy to recall: Sine equals Opposite over Hypotenuse, Cosine equals Adjacent over Hypotenuse, and Tangent equals Opposite over Adjacent. This mnemonic plays a crucial part in learning and applying trigonometric functions to solve problems involving right triangles.
💡Reciprocal Trigonometric Functions
Reciprocal trigonometric functions, introduced in the video, include cosecant, secant, and cotangent, each being the reciprocal of sine, cosine, and tangent, respectively. The video explains these concepts by inverting the ratios used in the original trigonometric functions, thereby expanding the toolkit for analyzing triangles and circles. These functions further deepen the understanding of trigonometric relationships by offering alternative perspectives on angle-side relationships.
💡Special Triangles
Special triangles, specifically the 30-60-90 and 45-45-90 triangles, are highlighted in the video as key tools for simplifying trigonometric calculations. These triangles have specific, predictable side ratios that make it easier to remember and apply the values of sine, cosine, and tangent for their angles. The discussion of these triangles serves to demonstrate practical examples of trigonometric functions in action and emphasizes their recurring nature in mathematics.
💡Sine
Sine is a trigonometric function that relates a right triangle's opposite side length to the length of its hypotenuse. The video describes sine (sin) of an angle theta as the ratio of the length of the leg opposite the angle to the hypotenuse. This function is pivotal for understanding circular and oscillatory motions, as well as for solving problems involving right triangles.
💡Cosine
Cosine is another trigonometric function, defined in the video as the ratio of the adjacent leg's length to the hypotenuse's length in a right triangle. Cosine (cos) plays an integral role in trigonometry, offering insights into the relationship between an angle and the sides of a triangle, and is essential in various applications ranging from physics to engineering.
💡Tangent
Tangent is a trigonometric function that relates the lengths of the opposite and adjacent sides of a right triangle. The video defines tangent (tan) as the ratio of the opposite side to the adjacent side. This function is particularly useful in situations where angles need to be calculated or analyzed without direct reference to the hypotenuse, showcasing its versatility in geometric and trigonometric problems.
Highlights

The framework highlights the mixed effects of modern technology, warning against overreliance on tech and outlining necessary guardrails.

The speaker emphasizes the importance of understanding technology's potential benefits as well as harms to thoughtfully navigate its continued emergence.

Notable distinction made between different types of AI systems, stating the need to evaluate each based on its capabilities and limitations.

Caution urged around anthropomorphizing AI and assuming human values, stating AI lacks consciousness and human context.

Suggests focused oversight and governance of high-risk AI applications to mitigate dangers while fostering innovation.

The framework outlines core principles of AI development: transparency, accountability, security, and ethics.

Stresses the importance of diversity and inclusion in the teams building AI systems to reduce harmful bias.

Calls for safeguards around AI use in critical public systems like healthcare, transportation and criminal justice.

Argues that AI can expand opportunities and empower people if guided by humanistic values and developed for social benefit.

Contends that AI should augment human capabilities and creativity rather than replace human roles and agency.

Urges investment in AI literacy and education to develop informed perspectives on technology's impacts.

Recommends legislation and global cooperation around AI safety standards and responsible development.

Calls for ethics boards and impact assessments to align AI systems with human values and societal good.

Argues for nuance in regulating AI, balancing precaution and permission to realize benefits while mitigating risks.

Stresses that AI should empower humanity, automating select tasks to liberate time for creativity and human connection.

Transcripts

Browse More Related Video

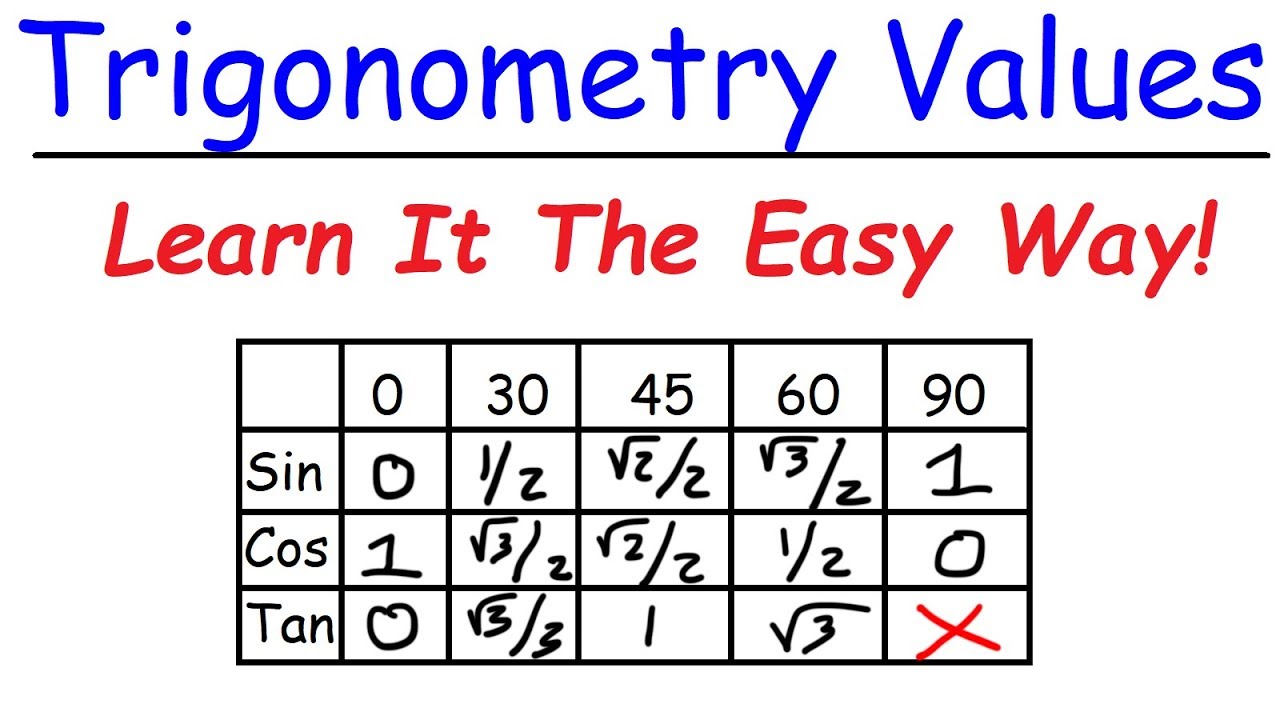
A Simple Trick To Remember Trigonometry Values

Trig - 0.6 Trig Functions of Acute Angles

How To Use Reference Angles to Evaluate Trigonometric Functions

30-60-90 Triangles - Special Right Triangle Trigonometry

Introduction to Right Triangle Trigonometry (Precalculus - Trigonometry 30)

Basic Trigonometry: Sin Cos Tan (NancyPi)

Rate This

5.0 / 5 (0 votes)

Thanks for rating: