The Easiest Way to Memorize the Trigonometric Unit Circle

Professor Dave Explains
3 Jan 201809:47
EducationalLearning
32 Likes 10 Comments

TLDRThe video introduces the unit circle, explaining how to easily derive trigonometric function values for angles by relating them to the circle's x and y coordinates. It overviews special triangles to derive common values like sine and cosine of pi/6. It then shows how visualizing movements around the coordinate plane reveals patterns for trig values in each quadrant, replacing fractions with roots to find a sequence. Using this sequence and recognizing coordinate relationships allows quickly evaluating any trig function. Comprehension checks at the end test retaining this intuitive understanding.

Takeaways
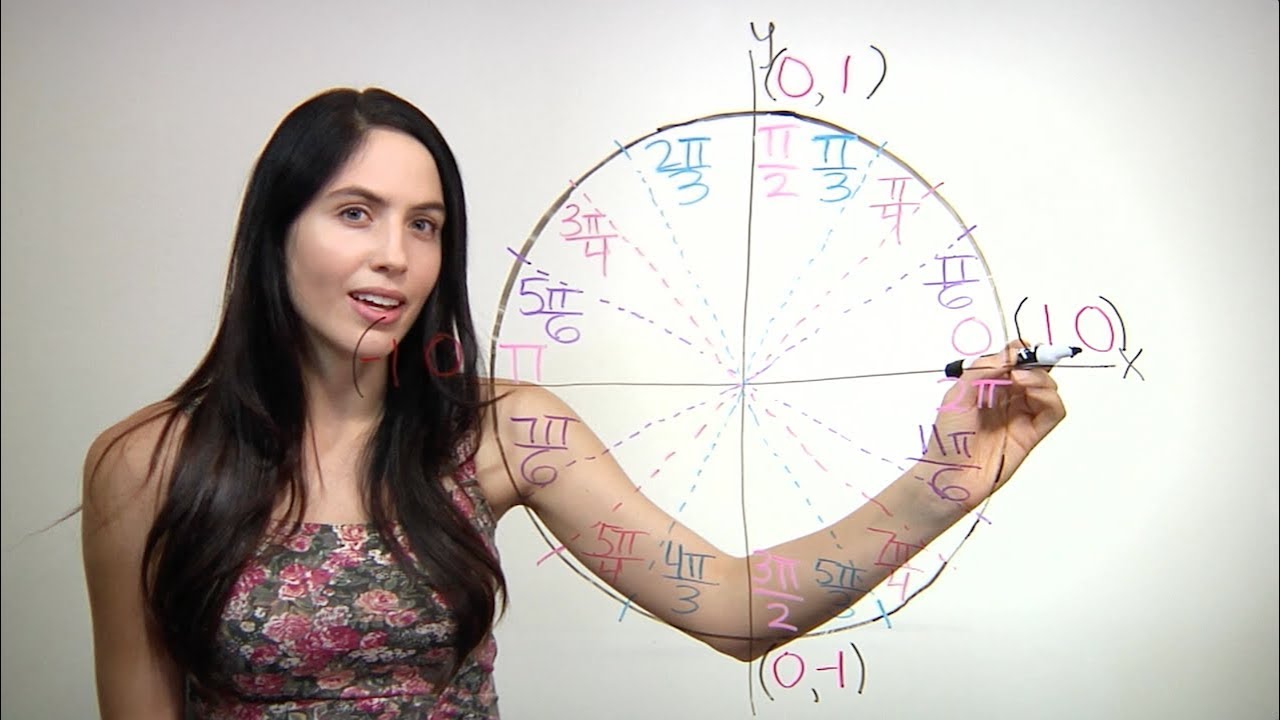
  • 😀 The unit circle is a circle with radius 1 centered at the origin of the coordinate plane.
  • 😎 The unit circle contains angles that are multiples of π/6 and π/4.
  • 🤓 Sine and cosine values correspond to the y and x coordinates on the unit circle.
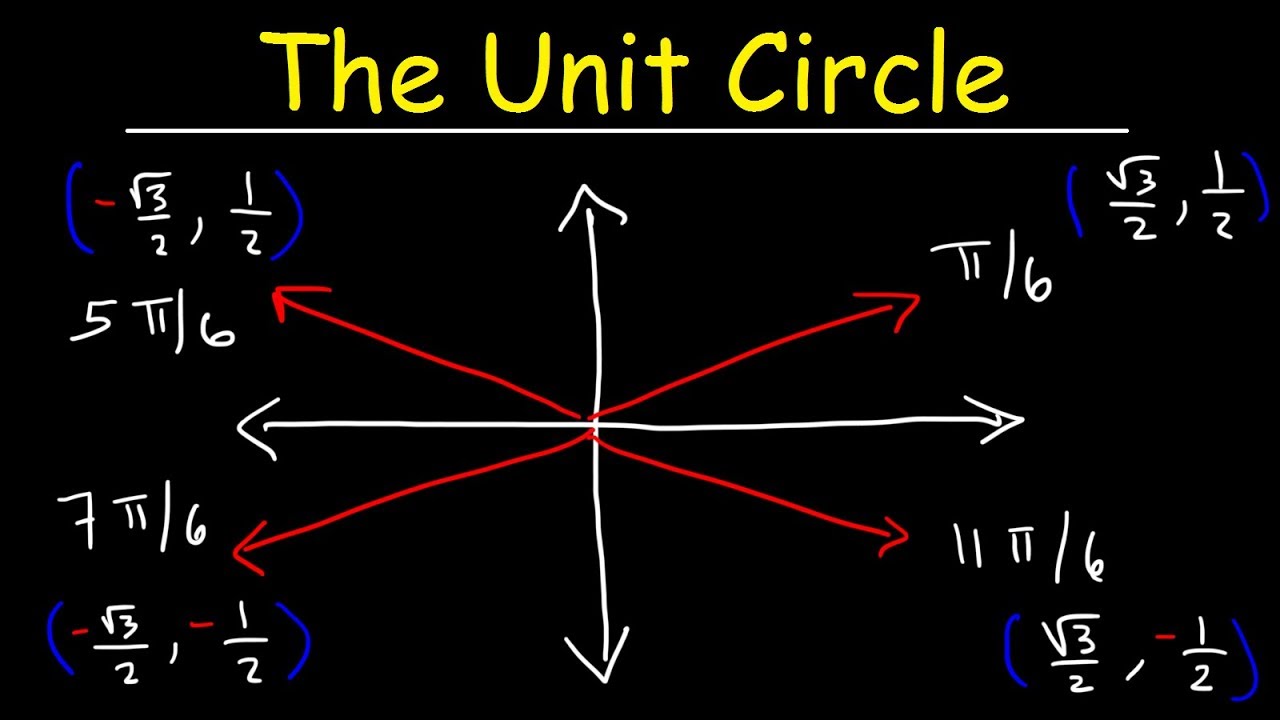
  • 🧐 Memorize the numeric sequence: root 0/2, root 1/2, root 2/2, root 3/2, root 4/2.
  • 🥸 Use this sequence for both sine (y) and cosine (x) values in quadrant 1.
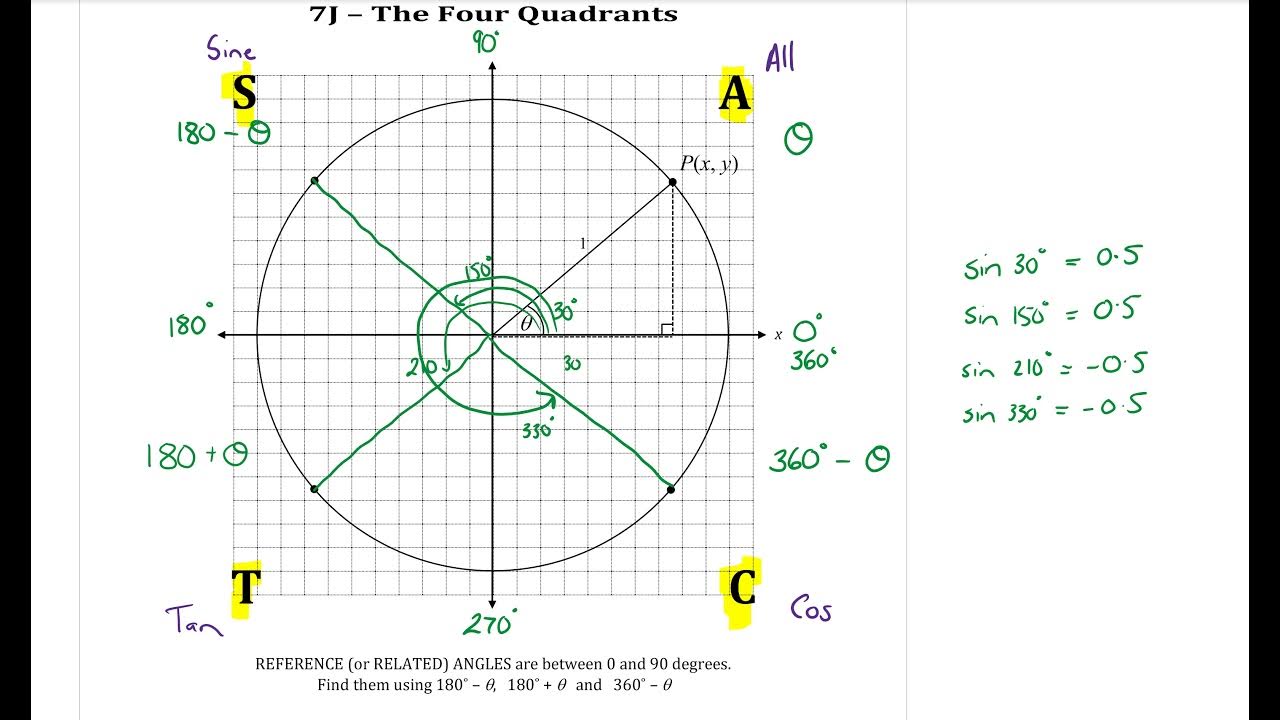
  • 😮 Sine stays positive and cosine becomes negative in quadrant 2.
  • 😲 Both sine and cosine become negative in quadrant 3.
  • 🤯 Cosine becomes positive again and sine stays negative in quadrant 4.
  • 👍 Visualize unit circle angles to quickly evaluate trig functions.
  • 💪 With practice, you'll easily evaluate trig functions for any angle!
Q & A

  • What is the unit circle?

    -The unit circle is a circle with a radius of 1 unit centered at the origin on the coordinate plane.

  • What do the X and Y coordinates on the unit circle represent?

    -The X coordinate represents the cosine of the angle and the Y coordinate represents the sine of the angle.

  • Why is pi/6 an important angle on the unit circle?

    -Pi/6, or 30 degrees, is important because it corresponds to the special 30-60-90 triangle, which makes its trig values easy to remember.

  • What pattern simplifies remembering unit circle values?

    -Replacing the fractions with roots creates a numerical sequence that matches the Y values then X values going counterclockwise around the circle.

  • How can you find sine, cosine, etc. for any angle?

    -Visualize the angle's location on the unit circle and use the coordinate at that point to find the function value, remembering sine = Y and cosine = X.

  • Why does the sine stay positive in quadrant 2?

    -The sine corresponds to the Y coordinate, which remains positive above the X axis in quadrant 2.

  • Why do the cosines become negative in quadrant 2?

    -The cosines correspond to X coordinates, which are negative to the left of the Y axis in quadrant 2.

  • How can you evaluate a trig function for a large angle?

    -Break it into whole revolutions plus a remaining part less than 2pi. Evaluate the trig function for just the remaining part.

  • What is cosecant defined as on the unit circle?

    -Cosecant is 1 over sine. So take the sine's Y value, flip it to find cosecant.

  • How can the unit circle help you memorize trig values?

    -By visualizing the angles and coordinate locations, you can intuitively remember sines, cosines, tangents without calculating.

Outlines
00:00
🤓 Introducing the Unit Circle

Paragraph 1 introduces the unit circle, explaining that it is a circle with radius 1 centered at the origin on the coordinate plane. It notes that the unit circle contains multiples of pi/6 and pi/4 whose sine and cosine values must be memorized. The paragraph then reviews what sine and cosine represent in terms of triangle side lengths and how this applies to the unit circle by constructing triangles.

05:03
😃 Memorizing Unit Circle Values

Paragraph 2 returns the unit circle values to simplified forms and extends them into the other quadrants. It notes patterns in the sine and cosine values that can help memorize them. The paragraph then demonstrates how to quickly evaluate trig functions for any angle on the unit circle by visualizing and locating reference angles.

Mindmap
Keywords
💡Unit circle
The unit circle is a circle with radius 1 centered at the origin on the coordinate plane. It is used to define trigonometric functions for all angles. Understanding and memorizing the unit circle is key for evaluating trig functions. The video walks through locating common angles on the unit circle and determining the sine and cosine values.
💡Trigonometric functions
Trigonometric functions like sine, cosine, tangent, etc. relate the angles and sides of a right triangle. They are defined using the unit circle. The video focuses on sine and cosine values for angles on the unit circle.
💡Coordinates
Each point on the unit circle has an x-coordinate equal to the cosine of the angle at that point, and a y-coordinate equal to the sine. So the coordinates directly give the trig values.
💡Quadrants
The coordinate plane is divided into 4 quadrants based on the sign of the x and y values. The video walks through how sine and cosine values change through the quadrants on the unit circle.
💡Special triangles
Certain angles like 30°, 45° and 60° have special triangle ratios that make their trig values easy to evaluate. The video uses these to motivate the unit circle values.
💡Reference angles
Reference angles help locate angles on the unit circle by giving the acute angle between the terminal side and the x-axis. They are useful for evaluating trig functions for angles in Quadrants II, III and IV.
💡Numerical sequence
The video introduces a numerical sequence (0, 1/2, √2/2, √3/2, 1) that encodes the common sine/cosine values on the unit circle. Memorizing this helps with visualization.
💡Trigonometric identities
Identities like sine squared + cosine squared = 1, or tan = sin/cos allow converting between different trig functions. They are used in the video for evaluating cosecant based on sine.
💡Radians
Radians are used as the unit for measuring angles on the unit circle rather than degrees. Multiples of π appear at various key angles.
💡Visualization
The ultimate goal is to be able to visually locate any angle on the unit circle and quickly determine trig values. This relies on ingraining the patterns.
Highlights

First significant highlight text

Second notable highlight text

Third innovative method introduced

Fourth theoretical contribution highlighted

Fifth notable impact discussed

Transcripts

Browse More Related Video

Trigonometric Functions of Any Angle - Unit Circle, Radians, Degrees, Coterminal & Reference Angles

Reciprocal Identities in Trigonometry (Precalculus - Trigonometry 9)

Yr 10 Trigonometry 10 - The four quadrants

How to Remember the Unit Circle (NancyPi)

The Unit Circle, Basic Introduction, Trigonometry

Trigonometric Functions: Sine, Cosine, Tangent, Cosecant, Secant, and Cotangent

Rate This

5.0 / 5 (0 votes)

Thanks for rating: