What is Integration? Finding the Area Under a Curve

Professor Dave Explains
18 Apr 201808:18
EducationalLearning
32 Likes 10 Comments

TLDRThe script provides an introduction to integral calculus and finding the area under a curve. It discusses how ancient mathematicians struggled with calculating areas bounded by curves, leading to the method of exhaustion using rectangles to approximate areas. The summation notation is introduced to represent the sum of the rectangular areas, taking the limit as the number of rectangles approaches infinity to find the precise area under a curve. This is connected back to differentiation as the inverse operation, unifying concepts from previous tutorials to demonstrate how calculus provides powerful mathematical tools.

Takeaways
  • πŸ˜€ Integration is the inverse operation of differentiation, just like addition/subtraction or multiplication/division.
  • πŸ˜ƒ Integration calculates the area under a curve between two points, while differentiation calculates the slope of the curve.
  • πŸ€” Ancient mathematicians realized calculating areas bounded by curves was tricky compared to polygons.
  • 😯 We can approximate the area under a curve using rectangles, and take the limit as the number of rectangles approaches infinity.
  • πŸ“ The summation notation Ξ£ represents adding up the areas of the rectangles under a curve from i=1 to n.
  • πŸ‘ As n increases, the sum of the rectangle areas approaches the true area under the curve.
  • πŸ“ˆ For the curve y=x^2 from 0 to 1, the area under the curve is 1/3.
  • 😊 Isaac Newton realized the deep connection between integration and differentiation, unifying calculus.
  • 🧠 Differentiation deals with rates of change, while integration finds accumulated change represented as area.
  • πŸ€“ Applying rectangles and limits to find areas under curves marked the beginning of integral calculus.
Q & A

  • What are the two key concepts that integral calculus connects?

    -Integral calculus connects the concepts of differentiation and integration, which are inverse operations like addition/subtraction and multiplication/division.

  • How did early mathematicians attempt to find the area under a curve?

    -Early mathematicians attempted to find the area under a curve using a method of exhaustion, approximating the area with thinner and thinner rectangles.

  • What is the summation notation used to represent the sum of the rectangular areas?

    -The uppercase Greek sigma βˆ‘ is used in the summation notation to represent adding up the areas of the rectangles.

  • How does increasing the number of rectangles help find the area under a curve?

    -Increasing the number of rectangles, while making them narrower, allows the sum of their areas to converge to the actual area under the curve.

  • What is the conceptual link between differentiation and integration?

    -Differentiation gives the slope of a curve at a point, while integration gives the area under the curve up to that point. They are inverse operations.

  • Who realized the connection between differentiation and integration?

    -Isaac Newton realized the deep connection between differentiation and integration, unifying centuries of calculus development.

  • What does the limit as n goes to infinity represent in the summation notation?

    -The limit as n goes to infinity represents allowing the number of rectangles to approach infinity, giving the exact area under the curve.

  • What are some applications of calculating the area under a curve?

    -Some applications include finding volumes of revolution, lengths of curves, and accumulated change over an interval.

  • What is the conceptual difference between differentiation and integration?

    -Differentiation gives an instantaneous rate of change, while integration sums up changes over an extended interval.

  • How did Newton's insights lead to modern calculus?

    -By articulating the link between differentiation and integration, Newton unified earlier mathematical concepts into the systematic field of calculus.

Outlines
00:00
πŸ˜€ Introducing Integration and Its Relation to Differentiation

This first paragraph introduces the concept of integration, explaining that it is the inverse operation of differentiation. It provides historical context, mentioning that mathematicians have been exploring integration for ages, back to the ancient Greeks. The key realization that linked integration and differentiation to create calculus is also noted. The paragraph concludes by stating that we will start by learning exactly what integration is.

05:01
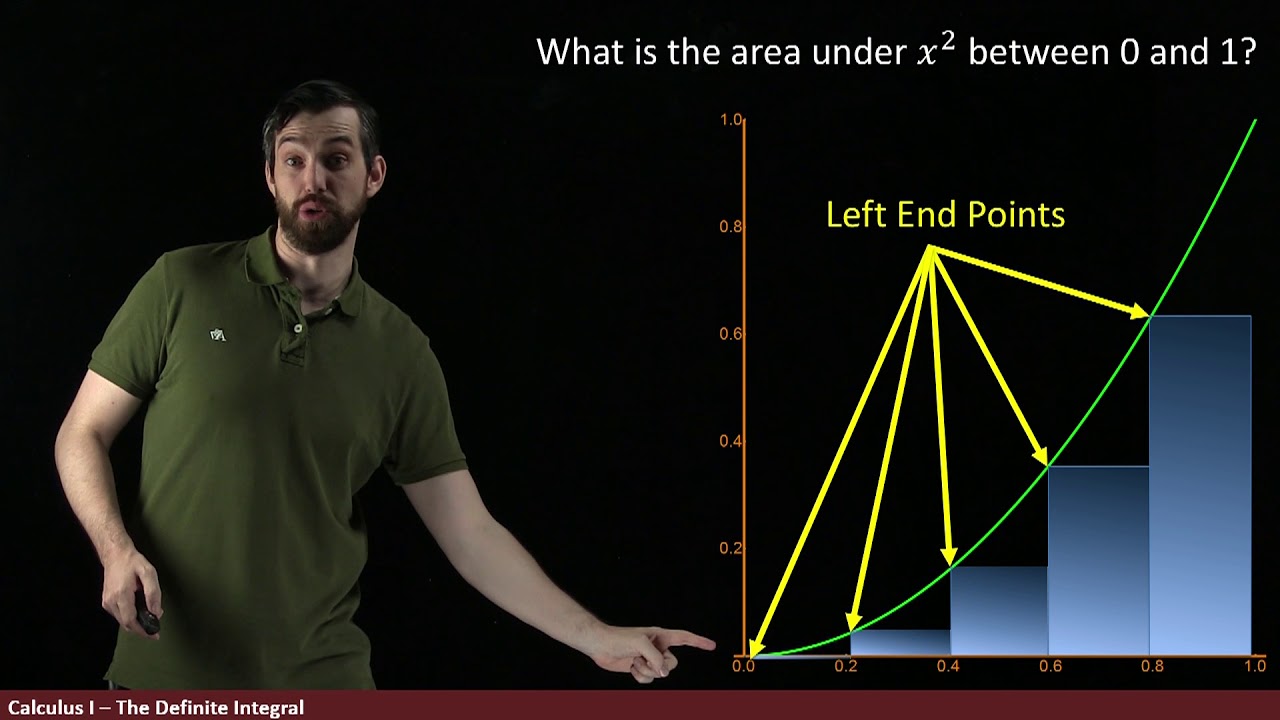
πŸ“ˆ Using Rectangles to Approximate the Area Under a Curve

This paragraph explains the geometrical concept of area under a curve and how it can be approximated using rectangles. It illustrates this visually, showing how more and narrower rectangles provide a closer estimate of the area. It also shows this quantitatively for the function y=x^2 from 0 to 1, demonstrating how the approximation converges to 1/3 as the number of rectangles approaches infinity. This leads to the summation notation to represent the area under any curve.

Mindmap
Keywords
πŸ’‘Integration
Integration refers to the mathematical operation of finding the area under a curve. It is presented in the video as an essential concept in integral calculus and a counterpart to differentiation in differential calculus. The narrator explains how integration allows us to approximate and precisely calculate the area under any curve over a particular interval using rectangles.
πŸ’‘Area
Area refers to the two-dimensional space enclosed within a given boundary, such as the area under a curve bounded by the function itself, the x-axis, and two vertical boundary lines. Calculating areas under curves is a key application of integration demonstrated in the video.
πŸ’‘Summation
Summation refers to the process of adding up multiple terms, often represented using sigma notation. In the context of integration and area approximation, it involves adding up the individual areas of multiple rectangles underneath a curve to obtain the total estimated area.
πŸ’‘Limit
Limit refers to the final value that a function approaches towards as an input variable reaches a particular value. In integration, we take the limit of the summation of rectangle areas as the number of rectangles approaches infinity. This limit gives us the precise non-approximate area under the curve.
πŸ’‘Curve
Curve refers to a non-straight continuous line whose shape is defined by a mathematical function. In integral calculus, we are often interested in finding areas bounded by curvy lines described by different functions rather than straight lines.
πŸ’‘Interval
Interval refers to the portion of the x-axis between two limits that bounds the area under the curve that we want to calculate. Integration allows us to find areas over any interval, not just standard geometric shapes.
πŸ’‘Approximation
Approximation refers to estimating an actual value by a sequence of values that get progressively closer to the actual value. In integration, we start with rough approximations of the area under a curve using a few rectangles, and improve the approximation by adding more rectangles.
πŸ’‘Rectangle
Rectangles refer to the simple geometric shapes that we use to approximate irregular areas under curves. As we use more rectangles that get infinitely narrow, the combined rectangle area approaches the actual area.
πŸ’‘Derivative
Derivatives describe the rate of change of a function and are a core concept in differential calculus. The video explains how integration links back to differentiation as an inverse mathematical operation.
πŸ’‘Inverse
Inverse operations are processes that 'undo' each other, such as subtraction undoing addition, or integration undoing differentiation. This deep connection unified the understanding of calculus as a coherent system.
Highlights

Researchers present an MRI study examining the effects of stimulant medication on reward processing in children with ADHD.

The study included 89 children with ADHD aged 8 to 12 years compared to 89 age-matched controls.

While on medication, children with ADHD showed normalized striatal responses during reward anticipation.

These findings suggest medication may normalize deficits in reward processing in ADHD.

The study had a double-blind, placebo-controlled, crossover design using two MRI scans.

Children were randomized to receive placebo or their usual stimulant medication on the first scan day.

On the second scan day, they received the opposite condition allowing for within-subject comparisons.

Reward processing was examined using a Monetary Incentive Delay task during fMRI scanning.

Medication normalized striatal responses during reward anticipation in the ADHD group.

Additionally, on medication the ADHD group showed similar ventral striatal responses to controls.

The findings provide evidence that stimulant medication may normalize reward-related neural deficits in ADHD.

Future work could examine the effects of medication on reward processing in other ADHD age groups.

The results have implications for understanding the pathophysiology and treatment of ADHD.

Overall, the study suggests medication may be beneficial in normalizing reward-related brain dysfunction in ADHD youth.

The double-blind placebo-controlled design lends confidence to the observed medication effects on brain function.

Transcripts

Browse More Related Video

The Definite Integral Part I: Approximating Areas with rectangles

AP Calculus AB: Lesson 6.2 Part 2 (Limit Definition of Definite Integral)

What Is an Integral?

The Definite Integral Part II: Using Summation Notation to Define the Definite Integral

Finding The Area Using The Limit Definition & Sigma Notation

Calculus 1 Lecture 4.3: Area Under a Curve, Limit Approach, Riemann Sums

Rate This

5.0 / 5 (0 votes)

Thanks for rating: