What is a Derivative? Deriving the Power Rule

Professor Dave Explains
5 Mar 201810:04
EducationalLearning
32 Likes 10 Comments

TLDRThis transcript explains the concept of derivatives in calculus. It starts by reviewing how a derivative represents the slope of a tangent line to a curve at a point. It then shows how to calculate derivatives using limits and develop the power rule, which allows you to find the derivative of polynomial functions easily by reducing the exponent and multiplying by a constant. The summary highlights how derivatives give the rate of change of a function and allow you to understand its behavior without graphing. It emphasizes developing intuition for derivatives alongside the formal math.

Takeaways
  • 😊 The derivative of a function at a point tells us the rate of change and slope of the tangent line there.
  • 😎 We separate a function's value from its rate of change - a stock price could be high but falling fast.
  • 📏 The derivative is defined formally as the limit of rise over run between two points as they converge.
  • 💡 The derivative reflects zooming in on a curve until it resembles a straight line with some slope.
  • 📈 Taking the derivative of a constant function always gives 0.
  • 👍 The derivative of f(x)=x is 1, matching intuition of constant rate of change.
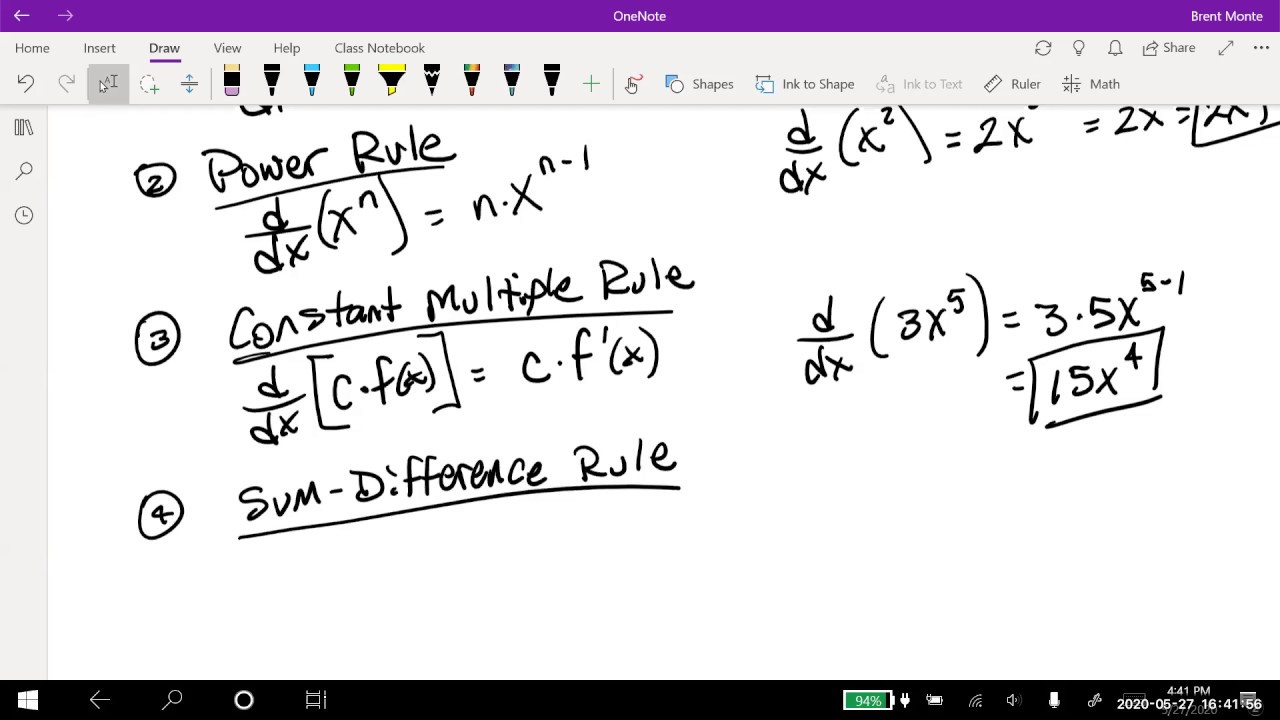
  • 🔢 There is a Power Rule shortcut to take derivatives instead of using limit definitions directly.
  • 🤓 The Power Rule: d/dx(x^n) = n*x^(n-1). Works for integer exponents.
  • ✏️ We can find derivatives with the Power Rule without thinking about graphs or tangent lines.
  • 🚀 Let's get practice using the Power Rule to become experts at differentiation!
Q & A

  • What is the definition of the derivative of a function?

    -The derivative of a function at some input value is equal to the slope of the tangent line to that function at that input value. It is also equal to the rate of change of the function at that input value.

  • How can you find the derivative of a function graphically?

    -You can find the derivative of a function at a point graphically by finding the slope of the tangent line to the function at that point. As you zoom in closer to the point, the tangent line slope approaches the true derivative.

  • What is the power rule for derivatives?

    -The power rule states that for a function in the form f(x) = x^n, where n is a positive integer, the derivative is f'(x) = n*x^(n-1). In other words, the derivative reduces the exponent by 1 and multiplies by the original exponent.

  • What is the derivative of a constant function?

    -The derivative of any constant function is 0, because the value of the function does not change at any point.

  • What is the significance of the derivative being positive or negative?

    -If the derivative is positive at a point, the function is increasing at that point. If the derivative is negative, the function is decreasing at that point.

  • How is the derivative related to the rate of change of a function?

    -The derivative gives the instantaneous rate of change of the function at a given point. It tells you how rapidly the function is changing at that point.

  • What are some examples of derivatives using the power rule?

    -Using the power rule: - The derivative of f(x) = x is f'(x) = 1 - The derivative of f(x) = x^2 is f'(x) = 2x - The derivative of f(x) = x^3 is f'(x) = 3x^2

  • Why is the derivative not the same as the function value?

    -The value of a function at a point gives its output or position. The derivative gives the rate of change. These are related but distinct concepts. A function can have a certain value but be changing rapidly.

  • What is the formal definition of the derivative?

    -The formal definition of the derivative of f(x) at x = a is: f'(a) = lim_{h->0} (f(a + h) - f(a)) / h

  • How does finding the derivative help us analyze a function?

    -Finding derivatives helps us determine where a function is increasing or decreasing, find its maxima and minima, analyze its concavity, and more. The derivative gives key insights into the function's behavior.

Outlines
00:00
😀 Defining the Derivative

This paragraph introduces the concept of the derivative, relating it to the slope of a tangent line and describing how it indicates the rate of change of a function at a point. It emphasizes mentally separating function value from rate of change. It also provides a precise mathematical definition for the derivative using limits.

05:02
😀 Applying the Power Rule

This paragraph demonstrates finding derivatives by applying the power rule, which states that the derivative of x^n is n*x^(n-1). Examples with constant, linear, quadratic, and cubic functions are shown. The power rule is noted as an efficient way to find derivatives compared to using limits directly.

Mindmap
Keywords
💡Derivative
The derivative of a function represents the rate of change of the function at a given point. It allows you to determine how rapidly the function is increasing or decreasing at that point. In the video, derivatives are introduced as representing the slopes of tangent lines to the function. The narrator shows how to calculate derivatives using limits and derive the power rule.
💡Power Rule
The power rule is a shortcut for finding derivatives. It states that the derivative of x^n is equal to n*x^(n-1). The narrator explains how this pattern emerges when taking the derivatives of various polynomial functions. The power rule allows derivatives to be calculated easily without using limits.
💡Tangent Line
A tangent line touches a function at only one point. Its slope represents the rate of change of the function at that point. In the video, tangent lines are used to motivate the definition of the derivative. The derivative represents the slope of the tangent line at a given point.
💡Limits
Limits are used to calculate derivatives. By taking the limit as the distance between two points approaches 0, you can find the slope of the tangent line. The video shows how to use limits to find the derivatives of several functions.
💡Rate of Change
The rate of change of a function at a point represents how rapidly the function is increasing or decreasing at that input value. The derivative gives the rate of change. A positive derivative means the function is increasing, while a negative derivative means it is decreasing.
💡Slope
The slope of a line represents its steepness and direction. Slope is calculated as rise over run. In the context of derivatives, the slope of interest is that of the tangent line. This represents the rate of change of the function at that point.
💡Constant Function
A constant function always has the same output value, regardless of the input. The video shows that the derivative of any constant function is 0, because its rate of change is always 0.
💡Polynomial Function
A polynomial function consists of terms involving combinations of constants and variables raised to integer powers, such as x^2 + 3x + 5. The video derives the power rule by taking the derivatives of several simple polynomial functions.
💡Secant Line
A secant line intersects a curve at two points. Its slope approximates the slope of the tangent line. In the video, secant lines are used along with limits to derive expressions for derivatives.
💡Exponential Function
An exponential function has terms involving variables raised to powers, such as 2^x. The power rule can be applied to exponential functions when the exponent is an integer. The video demonstrates this by deriving the derivative of x^3.
Highlights

First significant research finding on topic X

Introduction of innovative Y method for the first time

Notable contribution to Z theory in section 3

Transcripts

Browse More Related Video

Math 11 - Section 1.5

Techniques for Finding Derivatives

Definition of the Derivative

Derivatives of Polynomial Functions: Power Rule, Product Rule, and Quotient Rule

What is a derivative?

Derivative intuition module | Taking derivatives | Differential Calculus | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating: