The 4 Maxwell Equations. Get the Deepest Intuition!

Physics by Alexander FufaeV

5 Oct 201938:41

EducationalLearning

32 Likes 10 Comments

TLDRThis video introduces Maxwell's equations, the fundamental principles governing electricity and magnetism. It explains the concepts of electric and magnetic fields, how these fields interact with charges and currents, and the integral and differential forms of Maxwell's equations. The video covers key mathematical tools like partial derivatives and integrals, essential for understanding these equations. Through detailed explanations and examples, it demonstrates how electric and magnetic fields are interconnected and their crucial role in various applications, from electric cars to medical imaging. The video promises further exploration of electromagnetic waves and light in future content.

Takeaways

🔌 Maxwell's Equations are fundamental to understanding electricity and magnetism, underpinning a vast array of technologies from electric cars to MRI machines.
📚 The script aims to make Maxwell's Equations accessible, assuming the viewer has a basic understanding of partial derivatives and integrals.
🚀 Maxwell's Equations describe electric and magnetic fields, which are key to comprehending how electric charges interact with each other.
🔋 Coulomb's Law is introduced to define the electric force between two charges and is later used to derive the concept of electric field.
🧲 The electric field E is a vector quantity that represents the force a charge would experience at a given point in space.
🌀 The magnetic field B is introduced through the concept of a moving charge experiencing a force in a magnetic field, indicating the field's strength and direction.
🤔 The distinction between scalar and vector quantities is important, with vectors requiring both magnitude and direction for a full description.
🔄 The cross product is essential in determining the magnetic force on a moving charge, ensuring the force is always perpendicular to both the velocity and the magnetic field.
📐 Maxwell's Equations are presented in both integral and differential forms, suitable for different types of calculations and applications.
🌐 The divergence theorem is related to the sources and sinks of a field, while the curl theorem is about the rotation or circulation of a field around a loop.
🌀 The first Maxwell Equation relates the electric flux through a closed surface to the enclosed charge, leading to the concept that charges are the sources of electric fields.
🌐 The second Maxwell Equation states that the divergence of the magnetic field is always zero, implying there are no magnetic monopoles and that magnetic fields are generated by dipoles.
🔁 The third Maxwell Equation, Faraday's Law of Induction, connects a changing magnetic flux to the generation of an electric field, highlighting the interplay between electricity and magnetism.
⚡ The fourth Maxwell Equation shows that a magnetic field can be generated by both electric currents and changing electric fields, illustrating the dual nature of electromagnetic interactions.

Q & A

What are Maxwell's equations and why are they fundamental to many devices?
-Maxwell's equations are a set of four fundamental equations in physics that describe the behavior of both electric and magnetic fields, as well as their interactions with matter. They are fundamental to many devices because any device that exploits electricity or magnetism, such as electric cars, MRI machines, electric kettles, smartphone chargers, radios, and WiFi, is based on these equations.
What is the purpose of the video script?
-The purpose of the video script is to present Maxwell's equations in a simple and understandable way without deriving them theoretically or experimentally. It also aims to briefly explain the mathematics involved in the equations, such as partial derivatives and integrals.
What is Coulomb's law and how is it related to the electric field?
-Coulomb's law describes the electric force between two charged objects. It states that the force is directly proportional to the product of the charges and inversely proportional to the square of the distance between them. The electric field is derived from Coulomb's law by dividing the force by the charge of a test charge, which allows us to consider the force exerted by a source charge on a small test charge.

Outlines

00:00

🔋 Introduction to Maxwell Equations and Electric Fields

This video introduces various applications of electricity and magnetism, emphasizing that devices ranging from electric car engines to Wi-Fi rely on Maxwell equations. The goal is to simplify these equations for better understanding. The concept of electric fields is introduced using Coulomb's law, explaining how the electric force between two charged spheres can be calculated and how the electric field (E) is defined by eliminating the small charge (q) from Coulomb's law. The electric field's vector nature and its components in three-dimensional space (Ex, Ey, Ez) are also discussed.

05:01

🔀 Magnetic Fields and Force on Moving Charges

The magnetic field (B) and its effects on charged particles are explained. A moving charged particle in an external magnetic field experiences a magnetic force proportional to its charge, velocity, and the magnetic field. This relationship is expressed using vector cross product. The cross product of velocity and magnetic field vectors ensures the force is orthogonal to both. The magnetic field is described as a vector field, with its unit defined as Tesla. The relationship between electric and magnetic fields in Maxwell equations is established, highlighting their vector field nature.

10:05

🔄 Divergence Integral Theorem

The divergence integral theorem is introduced, linking surface and volume integrals. It explains the significance of surface integrals, scalar products, and how they measure the flux of a vector field through a surface. The theorem states that the sum of sources and sinks of a vector field within a volume equals the flux through the enclosing surface. The mathematical components, such as surface elements and the Nabla operator, are detailed, providing a comprehensive understanding of how electric and magnetic fields interact within a given volume.

15:08

🔁 Curl Integral Theorem

The curl integral theorem is discussed, focusing on how it relates to the rotation of vector fields. The theorem states that the total curl of a vector field within a surface equals the field's rotation along the surface's edge. This is essential for understanding the Maxwell equations. The theorem involves line integrals and surface integrals, emphasizing the orthogonal and parallel components of vector fields. The concepts of electric and magnetic voltages and their relation to energy changes in charged particles are explained.

20:13

📏 First Maxwell Equation and Divergence Form

The first Maxwell equation in integral form is introduced, stating that the electric flux through a closed surface equals the enclosed charge divided by the electric field constant. This equation is linked to Coulomb's law. The equation's transformation into differential form using the divergence integral theorem is explained. The differential form states that electric charges generate electric fields, highlighting the relationship between charge density and electric field divergence.

25:15

🧲 Second Maxwell Equation: Magnetic Monopoles

The second Maxwell equation, which states that the magnetic flux through a closed surface is always zero, is introduced. This implies that there are no magnetic monopoles, only magnetic dipoles with north and south poles. The differential form of this equation states that the divergence of the magnetic field is zero at all points in space. The theoretical implications and the potential discovery of magnetic monopoles are discussed.

30:20

🔄 Third Maxwell Equation: Faraday's Law of Induction

The third Maxwell equation, also known as Faraday's law of induction, is discussed. It relates the line integral of the electric field to the time derivative of the magnetic flux. This equation indicates that a changing magnetic flux generates an electric voltage. The relationship between electric and magnetic fields, energy conservation, and the significance of Lenz's law are explained. The differential form of this equation states that a changing magnetic field creates a rotating electric field and vice versa.

35:24

🔀 Fourth Maxwell Equation: Ampère's Law with Maxwell's Addition

The fourth Maxwell equation is introduced, stating that a rotating magnetic field is generated by electric currents and changing electric fields. The equation involves a line integral of the magnetic field and the contributions of current density and changing electric flux. The differential form of this equation states that the curl of the magnetic field is caused by current density and a changing electric field. The significance of this equation in understanding electrodynamics is highlighted.

Mindmap

Keywords

💡Maxwell Equations

The Maxwell Equations are a set of four fundamental equations in physics that describe how electric and magnetic fields are generated and altered by charges, currents, and changes in time. In the video, these equations are presented as the foundational basis for understanding various technologies and phenomena that exploit electricity and magnetism, such as electric cars, MRI machines, and wireless communication.

💡Electric Field

An electric field is a vector field surrounding electrically charged particles that exerts a force on other charged particles. In the video, the electric field is defined through Coulomb's law and is illustrated as the force a charge would experience when placed in the field. The concept is essential for understanding how electric forces act on charges and is a key component of the first Maxwell equation.

💡Magnetic Field

A magnetic field is a vector field that exerts a force on moving electric charges and magnetic dipoles. The video explains that the magnetic field is related to the force experienced by a charged particle moving through it, with the force being proportional to the charge, velocity, and the magnetic field's strength. The magnetic field is central to the third and fourth Maxwell equations.

💡Coulomb's Law

Coulomb's Law states that the electric force between two charged objects is proportional to the product of their charges and inversely proportional to the square of the distance between them. In the video, Coulomb's Law is used to derive the concept of the electric field and to explain how the force between charges is calculated.

💡Charge

A charge, in the context of the video, refers to the property of matter that gives rise to an electric field. There are two types of electric charges: positive and negative. The video discusses how the electric field is generated by charges and how the interaction between charges is fundamental to the understanding of electromagnetism.

💡Vector Fields

Vector fields are mathematical fields that assign a vector to each point in space, indicating both magnitude and direction. The video mentions both electric and magnetic fields as vector fields, emphasizing that they have components in three-dimensional space (Ex, Ey, Ez for electric field and Bx, By, Bz for magnetic field), which are crucial for understanding the spatial distribution of these fields.

💡Cross Product

The cross product is a binary operation on two vectors in three-dimensional space, resulting in a vector that is perpendicular to the plane containing the two input vectors. In the video, the cross product is used to describe the magnetic force on a moving charge, illustrating how the force is orthogonal to both the velocity of the charge and the magnetic field.

💡Divergence

In the context of vector calculus, divergence is a measure of the magnitude of a vector field's source or sink at a given point. The video explains the divergence as it relates to the Maxwell equations, specifically how the divergence of the electric field is related to the charge density, and the divergence of the magnetic field is always zero, indicating the absence of magnetic monopoles.

💡Curl

Curl is a vector operator that describes the rotation of a vector field around a particular point. The video discusses how the curl of the electric field is related to the time-varying magnetic field, and the curl of the magnetic field is related to both the electric current and the changing electric field, as described by the third and fourth Maxwell equations.

💡Integral Form and Differential Form

The Maxwell equations can be expressed in both integral and differential forms. The integral form involves surface and volume integrals and is suitable for calculating fields over a region, while the differential form involves derivatives and is useful for calculating fields at a single point. The video explains the transformation between these forms using the divergence and curl theorems, which are essential for understanding how to apply the Maxwell equations in various situations.

💡Electromagnetic Waves

Electromagnetic waves are a result of the interaction between changing electric and magnetic fields. While not explicitly detailed in the video script, the mention of these waves at the end suggests that the Maxwell equations can be used to derive the properties of these waves, which include light and other forms of electromagnetic radiation. The video implies that the equations reveal the wave-like nature of electromagnetic phenomena.

Highlights

Maxwell's equations are fundamental to devices exploiting electricity or magnetism, such as electric cars and MRI machines.

The video aims to present Maxwell's equations in a simple and understandable manner without deriving them theoretically or experimentally.

Understanding Maxwell's equations requires knowledge of partial derivatives and integrals.

Electric and magnetic fields are introduced as key concepts in Maxwell's equations, with electric field E defined by Coulomb's law.

The electric field E is a vector quantity with components in the x, y, and z directions, indicating force on a test charge at a specific location.

Magnetic field B is defined through the force experienced by a moving charged particle in an external magnetic field.

The unit of magnetic field strength is Tesla, derived from the force equation involving charge, velocity, and magnetic field.

Cross product is used to calculate the magnetic force on a charged particle, considering the orthogonality of force, velocity, and magnetic field.

Maxwell's equations are presented in both integral and differential forms, suitable for different calculation scenarios.

The divergence theorem is introduced to relate the volume integral of a vector field's divergence to the surface integral of its flux.

The curl theorem connects the line integral of a vector field around a surface to the surface integral of its curl.

The first Maxwell equation in integral form equates electric flux through a surface to the enclosed charge, leading to the differential form relating divergence of E to charge density.

The second Maxwell equation states that the divergence of the magnetic field B is always zero, implying no magnetic monopoles exist.

Faraday's law of induction is the third Maxwell equation in integral form, linking electric voltage around a loop to the change in magnetic flux through the surface enclosed by the loop.

The fourth Maxwell equation describes how electric currents and changing electric fields generate a magnetic field, with its differential form involving curl of B, current density, and changing electric field.

Maxwell's equations reveal the foundation of electrodynamics and have wide-ranging applications in technology and physics.

The equations also hint at the existence of electromagnetic waves, such as light, which is a topic for further exploration.

Transcripts

Browse More Related Video

Maxwell's Equations: Crash Course Physics #37

Magnetic Force Explained

Lectures 2 & 3 | Quantum Entanglements, Part 3 (Stanford)

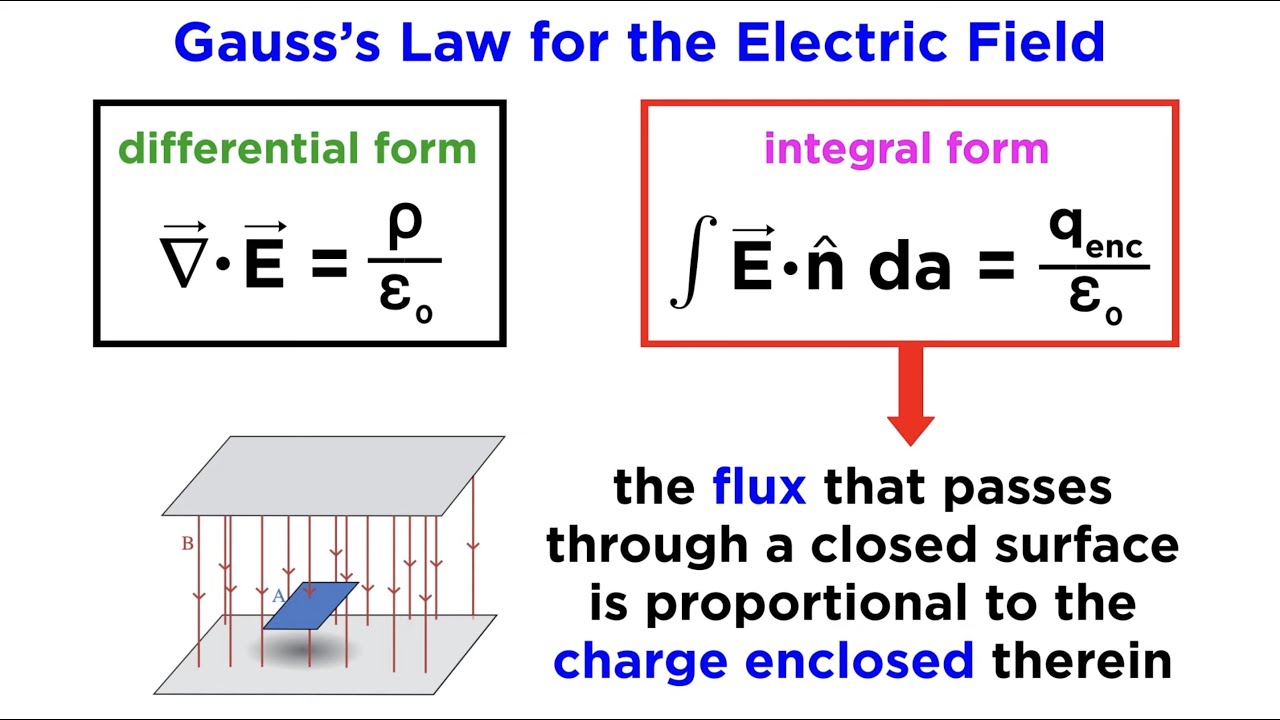
Maxwell’s Equations Part 1: Gauss’s Law for the Electric Field

What is Entropy, Electric & Magnetic Fields & Waves & Maxwell's Equations in Physics? - [1-1-2]

The Electromagnetic field, how Electric and Magnetic forces arise

Related Tags

Maxwell Equations Electrodynamics Electric Fields Magnetic Fields Coulomb's Law Faraday Induction Lenz's Law Physics Education Technical Theory Magnetic Resonance Electromagnetism Basics