5/4 Algebra 1 Zoom class
TLDRIn this educational video, the instructor leads a class through the vertical motion formula, a physics equation essential for understanding the parabolic trajectory of thrown or dropped objects. The session includes a worksheet with practice problems on quadratic equations and functions, emphasizing the significance of the vertex in graphing. Students are guided through solving for time and height, using the quadratic formula, and are reminded of an upcoming test. The instructor also clarifies the difference between problems involving thrown objects with initial velocities and those dropped without.
Takeaways
- 😀 The session is an algebra class focused on practicing the vertical motion formula, which is a physics formula used to calculate the height of an object at any given time.
- 📚 The class will work through practice problems related to quadratic equations and functions, specifically focusing on the motion formula and its application to problems involving thrown or dropped objects.
- 📈 There is an upcoming test on May 15th, and the class will have practice sessions and office hours to prepare for it, with a schedule provided for student reference.
- 📝 Students are expected to complete and submit work for grading by Friday, with specific problems assigned for this purpose.
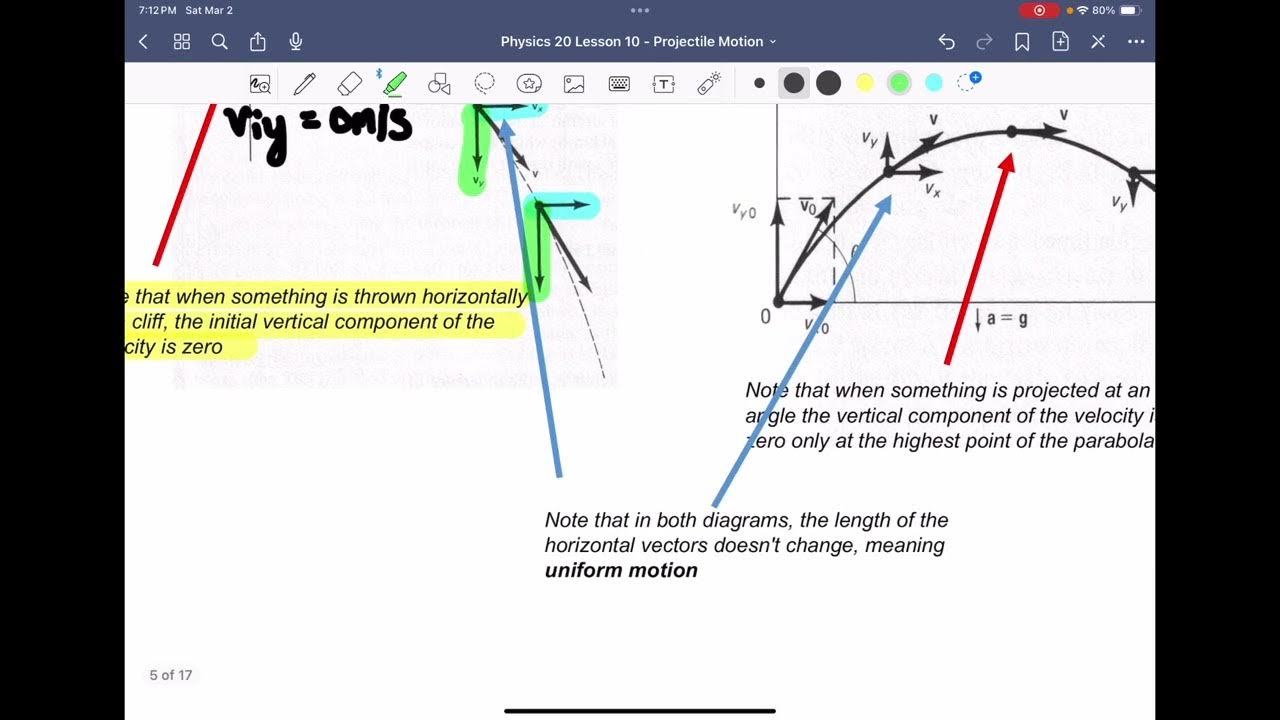
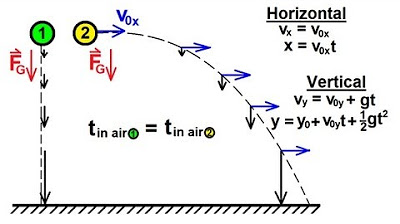
- 🔍 The vertical motion formula is given by \( H = -\frac{1}{2}gt^2 + v_0t + h_0 \), where \( H \) is the height, \( t \) is the time, \( g \) is the acceleration due to gravity, \( v_0 \) is the initial velocity, and \( h_0 \) is the initial height.
- 🌐 The formula includes a gravity constant, which is 32 feet per second squared in the U.S. and 9.8 meters per second squared outside the U.S.
- 📉 The class discusses how to set up and solve equations for specific scenarios, such as when an object hits the ground, using the vertical motion formula and the quadratic formula.
- 📊 The teacher demonstrates solving for the time it takes for an object to hit the ground and how to interpret the solutions in the context of the problem, dismissing negative time values as they are not physically meaningful.
- 📈 The vertex of the parabola, represented by the vertical motion formula, corresponds to the maximum height an object reaches, and the axis of symmetry can be used to find this point.
- 📚 The class also covers how to graph the height of an object over time, interpret the graph, and find specific points such as the vertex and the time when the object is at a certain height.
- 🔑 The importance of unit consistency is emphasized, ensuring that all measurements are in the same units (feet or meters) to avoid errors in calculations.
Q & A
What is the main topic of the video script?
-The main topic of the video script is the vertical motion formula, which is used to model the motion of objects thrown, dropped, or kicked, and its application in quadratic equations and functions.
What is the significance of the vertical motion formula in physics?
-The vertical motion formula is significant in physics as it describes the motion of objects under the influence of gravity, typically following a parabolic trajectory when thrown or dropped.
What are the variables in the vertical motion formula?
-The variables in the vertical motion formula are H for height, T for time, V_sub_zero for initial velocity, H_sub_zero for initial height, and g for the acceleration due to gravity.
Why is the value -1/2 multiplied by the gravity constant in the formula?
-The value -1/2 is multiplied by the gravity constant to account for the acceleration due to gravity in the vertical motion formula, which affects the object's height over time.
What is the value of the gravity constant used in the U.S. and what is its unit?
-In the U.S., the gravity constant used is 32 feet per second squared, which is derived from the standard gravity value of 9.8 m/s² when converted to feet.
What is the purpose of the initial velocity (V_sub_zero) in the formula?
-The initial velocity (V_sub_zero) in the formula represents the speed at which an object is thrown or kicked, and it affects the object's trajectory and height over time.
How does the script suggest simplifying the vertical motion formula for U.S. situations?
-The script suggests simplifying the vertical motion formula for U.S. situations by using the gravity constant value of 32 feet per second squared, which simplifies the formula to have a -16t² term.
What is the context of the problem involving Patti Patriot and the hot-air balloon festival?
-The context of the problem is a scenario where Patti Patriot is competing in a hot-air balloon festival and throws a marker from a balloon at an initial upward velocity of 32 feet per second from a height of 200 feet.
How does the script describe the process of finding the time it takes for an object to hit the ground?
-The script describes the process by setting the height of the object to zero in the vertical motion formula, solving the resulting quadratic equation, and selecting the positive solution for time, as negative time doesn't make sense in this context.
What is the vertex of a parabola in the context of the vertical motion formula?
-In the context of the vertical motion formula, the vertex of the parabola represents the maximum height an object reaches during its motion under the influence of gravity.
How does the script explain finding the vertex of the parabola formed by the vertical motion formula?
-The script explains finding the vertex by using the axis of symmetry formula, T = -B / 2A, and then plugging this time value back into the original equation to find the corresponding height.
What are the three main types of questions related to the vertical motion formula that students are expected to encounter?
-The three main types of questions are: finding the vertex of the parabola, determining the time it takes for an object to hit the ground, and interpreting the coordinates of the vertex in the context of the problem.
Why does the script emphasize the importance of units in the vertical motion formula?
-The script emphasizes the importance of units because the formula requires consistency in units, especially between the initial velocity, the gravity constant, and the height, to ensure accurate calculations.
How does the script handle the situation where an object is dropped instead of thrown?
-When an object is dropped, the script sets the initial velocity (V_sub_zero) to zero in the vertical motion formula and adjusts the formula accordingly to model the object's descent to the ground.
What is the significance of the quadratic formula in solving vertical motion problems?
-The quadratic formula is significant in solving vertical motion problems as it provides a method to find the time values when the object reaches certain heights, including when it hits the ground or reaches its maximum height.
How does the script address the possibility of negative time solutions in vertical motion problems?
-The script addresses negative time solutions by stating that they do not make sense in the context of time and should be disregarded, as time cannot be negative in these problems.
Outlines
📚 Algebra Class Introduction and Worksheet Overview
The instructor begins by greeting the students and sharing the number of attendees, noting that it's a good turnout. They introduce the plan for the class, which includes practicing problems from a worksheet related to quadratic equations and functions. The focus is on understanding the motion formula, specifically for vertical motion, which is applicable to physics problems involving thrown or dropped objects. The instructor also mentions an upcoming test and provides details about practice sessions and office hours for additional help. The summary of the first problem is given, which involves a hot-air balloon festival and a marker being thrown with an initial velocity from a certain height.
📘 Vertical Motion Formula and Its Components
The instructor explains the vertical motion formula, emphasizing its origin in physics and its relation to the parabolic trajectory of thrown or dropped objects. The formula is broken down into its variables, with 'H' representing height and 'T' for time. The constant values in the formula are discussed, particularly the gravity constant, which is 32 feet per second squared in the U.S. The instructor simplifies the formula for the U.S. context and introduces the variables for initial velocity (V sub 0) and initial height (H sub 0). The importance of these variables in solving problems is highlighted, with examples of different scenarios such as throwing from the ground level or from a height.
🔢 Problem-Solving Approach and Quadratic Formula Application
The class proceeds with solving a multi-part problem involving a marker thrown from a hot-air balloon. The instructor demonstrates how to set up the equation for the height of the marker in terms of time using the vertical motion formula. They address a student's question about the gravity constant and its application in different units. The instructor simplifies the equation and applies the quadratic formula to find the time it takes for the marker to hit the ground, rounding the answer to the nearest tenth and discussing the physical relevance of the solutions.
📉 Interpreting Quadratic Solutions and Contextual Reasoning
The instructor continues by discussing the interpretation of the solutions obtained from the quadratic formula, emphasizing that negative time values are not physically meaningful. They then introduce the task of graphing the height of the marker against time since it was thrown, explaining that the vertex of the parabola represents the maximum height. The process of finding the vertex from the function rule is outlined, and the maximum height is calculated by substituting the time value of the vertex back into the function.
📈 Graphing and Interpreting the Vertex of a Parabola
The focus shifts to graphing the height of the marker versus time, with the instructor explaining the significance of the vertex as the point of maximum height. They guide through the calculation of the vertex coordinates using the axis of symmetry formula derived from the quadratic equation. The vertex point's coordinates are found, and the instructor interprets these in the context of the problem, explaining the physical meaning of reaching the maximum height at a specific time.
🔑 Solving for Time and Height with Different Contexts
The script moves on to different scenarios, such as a case where keys are dropped from a height. The instructor modifies the vertical motion formula to account for the absence of initial velocity, resulting in a simpler equation. They demonstrate solving for the time it takes for the keys to hit the ground using the quadratic formula and discuss the physical interpretation of the solution. Additionally, they show how to find the time when the keys are 10 feet from the ground, emphasizing the importance of considering only positive, physically meaningful solutions.
📝 Reviewing Answer Keys and Understanding Problem Contexts
The instructor reviews answer keys for different problems, highlighting the importance of understanding the context and the units used in the problems. They address a student's question about discrepancies between the provided script and the answer key, clarifying the use of different formulas and units. The instructor also emphasizes the need to pay attention to the direction of initial velocities and the significance of the gravity constant in different regions.
🎈 Applying the Vertical Motion Formula to Various Scenarios
The script concludes with a discussion of additional problems involving the vertical motion formula, such as a water balloon being thrown downwards and a rock being launched from a building with a slingshot. The instructor points out the need to adjust the formula based on the initial velocity and direction, as well as the units of measurement. They also mention the possibility of obtaining two positive solutions for certain problems and the importance of considering both in the context of the scenario.
👋 Wrapping Up the Class and Encouraging Office Hours
In the final part of the script, the instructor wraps up the class by summarizing the tasks for the students, which include working on problems 2 and 4. They remind students of the office hours available for additional help and encourage them to ask questions if they encounter difficulties. The instructor wishes the students a happy Star Wars day and a good afternoon, indicating the end of the session.
Mindmap
Keywords
💡Vertical Motion Formula
💡Height (H)
💡Time (T)
💡Quadratic Equation
💡Initial Velocity (V₀)
💡Initial Height (H₀)
💡Gravity Constant
💡Parabolic Pattern
💡Vertex
💡Quadratic Formula
Highlights
Introduction to a virtual algebra class with an agenda for the day's activities.
Explanation of the vertical motion formula, its relevance in physics, and its application in quadratic equations.
The significance of the vertex in quadratic functions and its relation to the maximum height in vertical motion problems.
A test announcement for May 15th and the schedule for practice and review sessions leading up to the test.
Practice problems involving the vertical motion formula, emphasizing the importance of matching units in calculations.
The process of setting up and solving equations to find the time it takes for an object to hit the ground.
Use of the quadratic formula to solve for time in vertical motion problems, with a step-by-step demonstration.
The concept of extraneous solutions in the context of time, explaining why negative time values are not valid.
Differentiating between problems involving objects being thrown, dropped, or kicked, and adjusting the initial velocity in the formula accordingly.
A detailed walkthrough of a problem involving a hot-air balloon festival, integrating concepts of initial velocity, height, and time.
The method for finding the vertex of a parabola, which represents the maximum height in vertical motion problems.
Interpreting the vertex coordinates in the context of a problem, relating them to real-world scenarios.
A unique problem involving a character named Mary Mustang dropping keys, emphasizing the importance of initial conditions in problem-solving.
The distinction between using the quadratic formula and factoring in different types of vertical motion problems.
An example of calculating the time it takes for an object to reach a certain height, not just when it hits the ground.
A summary of the key concepts students are expected to understand, including the vertex, time to hit the ground, and the interpretation of solutions.
A closing Q&A session addressing student queries about the material covered and clarification on problem-solving steps.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: