Equation of Motion : How to Select the Right Equation?

Manocha Academy

24 Apr 202049:37

EducationalLearning

32 Likes 10 Comments

TLDRIn this educational video, the instructor guides students through selecting the appropriate equation of motion for various scenarios. The script covers the fundamental difference between distance and displacement, speed and velocity, and emphasizes the importance of understanding when to apply each equation. The class delves into the equations of motion, particularly useful for accelerated motion, and provides examples to illustrate the selection process. The instructor also discusses special cases like freely falling bodies and upwardly thrown objects, highlighting the constant acceleration due to gravity in these instances.

Takeaways

📚 The class focuses on teaching students how to select the correct equation of motion for various physics problems involving motion.
🔍 The instructor emphasizes the importance of understanding the difference between distance (a scalar) and displacement (a vector), as well as speed (a scalar) and velocity (a vector).
📐 The equations of motion discussed are v = u + at, s = ut + (1/2)at^2, and v^2 = u^2 + 2as, which are used to solve problems involving uniformly accelerated motion.
🚀 The class clarifies that the equations of motion are applicable to scenarios with uniform acceleration or deceleration, but not for non-uniform acceleration or when acceleration is changing.
📉 For a freely falling body, the acceleration is represented by g (or a in some contexts) and is approximately 9.8 m/s^2 or rounded to 10 m/s^2 for simplicity.
📈 When a body is thrown upwards, the acceleration is considered negative, reflecting the retardation (or deceleration) due to gravity acting in the opposite direction of motion.
🔢 The instructor provides a step-by-step approach to solving problems using the equations of motion, which includes writing down the data, selecting the appropriate equation, and then substituting the values to find the unknown.
📝 Examples are given to illustrate how to apply the equations of motion, such as finding the speed of a car after a certain time with uniform acceleration, and calculating the height of a building from which a ball is dropped.
🤓 The class encourages active participation, with students being prompted to answer questions and engage in discussions to reinforce their understanding of the concepts.
🌐 The instructor mentions Manoj Academy's website and upcoming courses in chemistry and math, inviting students to subscribe and participate in the live classes for further learning.

Q & A

What are the three basic equations of motion discussed in the class?
-The three basic equations of motion discussed are: 1) V = u + at, 2) s = ut + 0.5at^2, and 3) V^2 = u^2 + 2as.
What is the difference between distance and displacement?
-Distance is the total length of the path traveled by an object, while displacement is the straight-line distance from the initial to the final position of the object, having both magnitude and direction.
When is the distance traveled by an object equal to its displacement?
-The distance traveled by an object is equal to its displacement when the object moves in a straight line path.
What are the scalar and vector quantities?
-Scalar quantities have only magnitude, such as distance. Vector quantities have both magnitude and direction, such as displacement and velocity.
What is the difference between speed and velocity?
-Speed is the rate of change of distance with time and is a scalar quantity. Velocity is the rate of change of displacement with time and is a vector quantity, including direction.
When can the simple formulas for speed and velocity be used?
-The simple formulas for speed and velocity can be used when an object is moving with constant speed or constant velocity, meaning the acceleration is zero.
What is acceleration and what is its value when an object is moving at a constant speed?
-Acceleration is the rate of change of velocity with time. When an object is moving at a constant speed, the acceleration is zero.
What is the difference between average speed and instantaneous speed?
-Average speed is the total distance traveled divided by the total time taken. Instantaneous speed is the speed of an object at a specific moment in time.

Outlines

00:00

📚 Introduction to Equations of Motion

The instructor begins by welcoming students to a class focused on selecting the appropriate equation of motion. Common equations such as v = u + at, s = ut + 1/2at^2, and v^2 = u^2 + 2as are introduced, and the instructor promises to guide students on choosing the correct equation for various problems. The video also promotes Manoj Academy's website and upcoming courses in chemistry and maths, encouraging viewers to subscribe and participate in live classes.

05:04

🔍 Clarifying Distance, Displacement, Speed, and Velocity

The script delves into the differences between distance and displacement, defining distance as the length of the path traveled and displacement as the shortest distance from the initial to the final position. It also contrasts speed and velocity, with speed being a scalar (having only magnitude) and velocity being a vector (having both magnitude and direction). The conditions under which distance equals displacement, such as straight-line motion, are discussed, along with the scalar and vector nature of time and acceleration.

10:05

📘 Understanding the Context of Equations of Motion

The instructor explains that the equations of motion are typically used in the context of straight-line motion, where distance and displacement are equivalent. It is clarified that these equations apply to scenarios involving constant acceleration or deceleration, but not when acceleration is changing non-uniformly. The concepts of initial and final velocities and the importance of direction in vector quantities are emphasized.

15:06

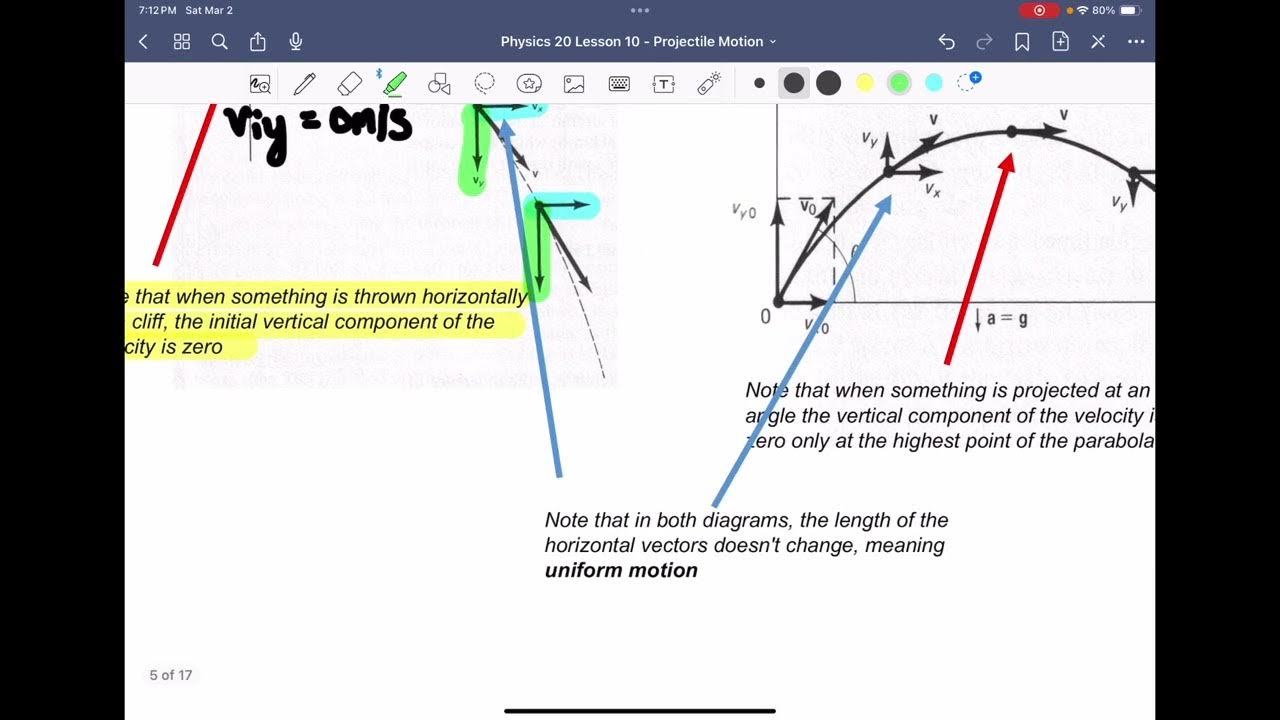
🚀 Applying Equations of Motion to Free Fall and Thrown Bodies

The script discusses the application of the equations of motion to freely falling bodies and bodies thrown upwards. It highlights the importance of using the correct value and sign for acceleration due to gravity (g), which is positive for free fall and negative for upward throws. The distinction between the equations' applicability to uniform motion and non-uniform motion is made, with the equations being suitable for constant acceleration scenarios.

20:08

📝 Solving Motion Problems Using Equations of Motion

The instructor guides students through the process of solving motion problems by first writing down the given data and the unknowns, then selecting the appropriate equation of motion based on the symbols present. An example problem involving a car starting from rest with a uniform acceleration is used to illustrate the steps of writing down data, selecting the equation, and substituting values to find the final velocity.

25:09

🏢 Calculating the Height of a Building from Free Fall

The script presents a problem where a ball is dropped from the top of a building, and students are tasked with finding the building's height. The initial velocity of the ball is identified as zero, and the acceleration due to gravity is used in the second equation of motion to calculate the displacement, which corresponds to the building's height. The process of writing down the data, selecting the correct equation, and solving for the unknown is emphasized.

30:12

🚀 Determining the Initial Velocity for Maximum Height in Upward Throws

The instructor discusses how to find the initial velocity needed for a ball to reach a maximum height when thrown upwards. The problem involves using the third equation of motion, considering the final velocity at the top of the throw to be zero. The importance of using the correct acceleration value with the appropriate sign is highlighted, and the process of substitution in the equation is outlined to find the initial velocity.

35:12

🔢 Simplifying Calculations with Smart Mathematics

The script demonstrates a technique for simplifying calculations in physics problems, using the example of finding the initial velocity for a ball thrown to a certain height. The instructor advises students to look for common factors and to use approximations for square roots, such as recognizing that √2 is approximately 1.41, to quickly arrive at the correct answer without a calculator.

40:13

🤔 Engaging with the Classroom: Free Fall and Retardation Problems

The instructor poses questions to the students regarding the characteristics of a freely falling body and a car's retardation after braking. The goal is to encourage student participation and to apply the concepts learned in the class. The questions are designed to reinforce the understanding of constant acceleration in free fall and the calculation of deceleration based on changes in velocity and displacement.

45:16

👋 Closing Remarks and Encouragement for Continued Learning

In the closing segment, the instructor thanks students for their participation, encourages them to continue learning, and to balance their studies with leisure during the lockdown. The instructor also promotes upcoming courses on Manoj Academy's website and invites students to subscribe to the YouTube channel for notifications about new content and live classes.

Mindmap

Keywords

💡Equations of Motion

The equations of motion are fundamental principles in physics that describe the relationship between the velocities, positions, and time of an object undergoing motion. In the video, these equations are central to understanding how to analyze different types of motion, such as constant speed and accelerated motion. The script discusses three specific equations: V = U + AT, S = UT + 1/2 AT^2, and V^2 = U^2 + 2AS, which are used to determine the final velocity, displacement, and the effect of acceleration on an object's motion.

💡Displacement

Displacement is a vector quantity that refers to the change in position of an object from its initial to its final position, typically represented by a straight line and having both magnitude and direction. In the video, displacement is contrasted with distance, and it is used to illustrate the path an object takes during motion, especially in the context of the equations of motion.

💡Distance

Distance is a scalar quantity that represents the total length of the path traveled by an object, regardless of the direction of motion. In the script, the instructor clarifies that while distance is a straightforward measure, it can differ from displacement if the path is not straight. The concept is essential when discussing whether distance can equal displacement in cases of straight-line motion.

💡Velocity

Velocity is a vector quantity that describes the rate of change of an object's position, which includes both speed and direction. The video script explains that velocity is the displacement divided by the time and contrasts it with speed, emphasizing that velocity conveys more information about an object's motion due to its directional component.

💡Speed

Speed is a scalar quantity that measures how fast an object is moving, without considering the direction of motion. In the video, speed is defined as the distance traveled per unit of time and is used to describe situations where an object moves with a constant velocity, which is when the equations of motion simplify to basic speed and distance relationships.

💡Acceleration

Acceleration is a vector quantity that represents the rate of change of velocity per unit time. In the context of the video, acceleration is crucial for understanding how the velocity of an object changes over time, especially when the motion is not uniform. The script mentions that the equations of motion are particularly useful for scenarios involving constant acceleration or deceleration.

💡Freely Falling Body

A freely falling body is an object that is in motion solely under the influence of gravity, starting from rest. The video script uses this term to describe situations where objects are dropped and fall straight down, accelerating due to gravity. The concept is important for understanding the constant acceleration of such bodies near the Earth's surface, which is approximately 9.8 m/s^2.

💡Retardation

Retardation, also known as deceleration, is the decrease in an object's speed over time, often due to an opposing force such as friction or gravity acting in the opposite direction of motion. In the video, retardation is discussed in the context of a car braking and slowing down, which is an example of negative acceleration.

💡Scalar and Vector Quantities

Scalar quantities have only magnitude and no direction, such as distance and speed, while vector quantities have both magnitude and direction, such as displacement and velocity. The video script emphasizes the importance of understanding whether a physical quantity is scalar or vector, as this affects how it is represented and used in the equations of motion.

💡Uniform Motion

Uniform motion refers to the movement of an object at a constant speed in a straight line, without acceleration. In the video, uniform motion is contrasted with accelerated motion, and the script explains that the simple formulas for speed and distance are typically used for uniform motion, whereas the equations of motion are reserved for more complex scenarios involving acceleration.

💡Non-Uniform Motion

Non-uniform motion is motion where the speed or direction of an object changes over time, often due to acceleration or deceleration. The video script discusses that the equations of motion are not suitable for non-uniform motion where the acceleration is changing, as these equations assume constant acceleration.

Highlights

Introduction to the class focusing on selecting the correct equation of motion.

Explanation of the three basic equations of motion: V = u + at, s = ut + 1/2at^2, and V^2 = u^2 + 2as.

Tips and techniques for choosing the appropriate equation of motion for a given problem.

Promotion of Manoj Academy's website and upcoming chemistry and math courses.

Difference between distance and displacement, with distance being a scalar and displacement a vector.

Condition when distance equals displacement, which is when the path is a straight line.

Comparison of speed and velocity, with speed being a scalar and velocity a vector.

Use of simple speed and velocity formulas for constant speed or velocity scenarios.

Introduction to the concept of acceleration, its definition, and its role in motion.

Equations of motion applicable for uniform acceleration and retardation, but not for non-uniform acceleration.

Special case of freely falling bodies and the use of gravity as a constant acceleration.

Difference in acceleration values for upward and downward motions.

Methodology for solving motion problems using equations of motion, emphasizing data analysis and equation selection.

Example problem solving: finding the speed of a car after a minute with uniform acceleration.

Example problem solving: calculating the height of a building from which a ball is dropped.

Example problem solving: determining the initial speed required for a ball to reach a maximum height.

Homework problem presented: calculating the retardation of a car during braking.

Encouragement for students to participate in live classes and provide feedback for future topics.

Closing remarks with well-wishes for health and encouragement for balanced study during lockdown.

Transcripts

Browse More Related Video

Physics 20 Unit A Lesson 10: Projectile Motion

Equations of Motion Sums

Motion Class 9 Physics

Kinematics Part 2: Vertical Motion

Deriving the Range Equation of Projectile Motion

2021 Live Review 8 | AP Physics C: Mechanics | Understanding Resistive Forces

Related Tags

Equations of Motion Physics Class Educational Content Motion Analysis Classroom Techniques Velocity Concepts Acceleration Basics Displacement Study Manoj Academy Interactive Learning