Product To Sum Identities and Sum To Product Formulas - Trigonometry

The Organic Chemistry Tutor
20 Oct 201713:24
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script focuses on simplifying trigonometric expressions using product-to-sum and sum-to-product formulas. It introduces four key formulas for each category and demonstrates their application through examples, such as simplifying sine 7x times sine 4x and sine 9x times cosine 3x. The script also covers sum-to-product formulas, illustrating their use with examples like sine 8x plus sine 3x and cosine 11x plus cosine 3x. Additionally, it provides a verification of the identity involving sine and cosine functions, proving that sine x plus sine 3x divided by cosine x plus cosine 3x equals tangent 2x. The emphasis is on understanding and applying these formulas to solve trigonometric problems efficiently.

Takeaways
  • 📚 The video script introduces four product-to-sum trigonometric formulas that are essential for simplifying expressions.
  • 🔍 The first formula presented is \( \sin(\alpha)\cos(\beta) = \frac{1}{2}(\cos(\alpha - \beta) - \cos(\alpha + \beta)) \).
  • 📈 The second formula is \( \cos(\alpha)\cos(\beta) = \frac{1}{2}(\cos(\alpha - \beta) + \cos(\alpha + \beta)) \), with a positive sign for the sum of angles.
  • 📉 The third formula is \( \sin(\alpha)\cos(\beta) = \frac{1}{2}(\sin(\alpha + \beta) + \sin(\alpha - \beta)) \), using sine instead of cosine.
  • ➗ The fourth and final formula is \( \cos(\alpha)\sin(\beta) = \frac{1}{2}(\sin(\alpha + \beta) - \sin(\alpha - \beta)) \).
  • 🧩 The script demonstrates how to apply these formulas to simplify specific trigonometric expressions, such as \( \sin(7x) \cdot \sin(4x) \).
  • 📝 Another example given is simplifying \( \sin(9x) \cdot \cos(3x) \) using the product-to-sum formula.
  • 🤔 The video also covers sum-to-product formulas, which are used to transform sums or differences of trigonometric functions into products.
  • 📐 Examples of simplifying expressions using sum-to-product formulas include \( \sin(8x) + \sin(3x) \) and \( \cos(11x) + \cos(3x) \).
  • 📉 The script provides a step-by-step guide on simplifying \( \sin(75^\circ) + \sin(15^\circ) \) using the sum-to-product formula.
  • 🔑 A verification identity problem is tackled, showing that \( \frac{\sin(x) + \sin(3x)}{\cos(x) + \cos(3x)} \) is equal to \( \tan(2x) \).
Q & A

  • What are the four product-to-sum formulas mentioned in the script?

    -The four product-to-sum formulas are: 1) sin(α)cos(β) = 1/2[cos(α-β) - cos(α+β)], 2) cos(α)cos(β) = 1/2[cos(α-β) + cos(α+β)], 3) sin(α)cos(β) = 1/2[sin(α+β) + sin(α-β)], and 4) cos(α)sin(β) = 1/2[sin(α+β) - sin(α-β)].

  • How can we simplify the expression sin(7x)sin(4x) using product-to-sum formulas?

    -Using the formula sin(α)sin(β) = 1/2[cos(α-β) - cos(α+β)], and identifying α as 7x and β as 4x, the expression simplifies to 1/2[cos(7x-4x) - cos(7x+4x)] which is 1/2[cos(3x) - cos(11x)].

  • What is the simplified form of sin(9x)cos(3x) using product-to-sum identities?

    -By using the formula sin(α)cos(β) = 1/2[sin(α+β) + sin(α-β)], and identifying α as 9x and β as 3x, the expression simplifies to 1/2[sin(9x+3x) + sin(9x-3x)] which is 1/2[sin(12x) + sin(6x)].

  • What are the sum-to-product formulas that are necessary to know according to the script?

    -The sum-to-product formulas to know are: 1) sin(α) + sin(β) = 2sin[(α+β)/2]cos[(α-β)/2], 2) sin(α) - sin(β) = 2sin[(α-β)/2]cos[(α+β)/2], 3) cos(α) + cos(β) = 2cos[(α+β)/2]cos[(α-β)/2], and 4) cos(α) - cos(β) = -2sin[(α+β)/2]sin[(α-β)/2].

  • How do we simplify the expression sin(8x) + sin(3x) using sum-to-product formulas?

    -Using the formula sin(α) + sin(β) = 2sin[(α+β)/2]cos[(α-β)/2], and identifying α as 8x and β as 3x, the expression simplifies to 2sin[(8x+3x)/2]cos[(8x-3x)/2] which is 2sin(11x/2)cos(5x/2).

  • What is the simplified form of cos(11x) + cos(3x) according to the sum-to-product identities?

    -By using the formula cos(α) + cos(β) = 2cos[(α+β)/2]cos[(α-β)/2], and identifying α as 11x and β as 3x, the expression simplifies to 2cos[(11x+3x)/2]cos[(11x-3x)/2] which is 2cos(7x)cos(4x).

  • How do we simplify the expression sin(75°) + sin(15°) using sum-to-product formulas?

    -Using the formula sin(α) + sin(β) = 2sin[(α+β)/2]cos[(α-β)/2], and identifying α as 75° and β as 15°, the expression simplifies to 2sin[(75°+15°)/2]cos[(75°-15°)/2] which is 2sin(45°)cos(30°), and the exact value is √6/2 after canceling out the common factors.

  • What identity are we trying to verify in the script's verifying identity problem?

    -We are trying to verify the identity sin(x) + sin(3x) / [cos(x) + cos(3x)] = tan(2x).

  • How does the script suggest simplifying the top part of the fraction in the verifying identity problem?

    -The script suggests using the sum-to-product formula for sine, which is sin(α) + sin(β) = 2sin[(α+β)/2]cos[(α-β)/2], with α as 3x and β as x, resulting in 2sin(2x)cos(x).

  • How does the script suggest simplifying the bottom part of the fraction in the verifying identity problem?

    -The script suggests using the sum-to-product formula for cosine, which is cos(α) + cos(β) = 2cos[(α+β)/2]cos[(α-β)/2], with α as x and β as 3x, resulting in 2cos(2x)cos(x).

  • What is the final simplified form of the verifying identity problem in the script?

    -After simplification, the fraction becomes tan(2x), which verifies the identity sin(x) + sin(3x) / [cos(x) + cos(3x)] = tan(2x).

Outlines
00:00
📚 Trigonometric Product to Sum Formulas

This paragraph introduces four trigonometric product to sum formulas, which are essential for simplifying expressions involving trigonometric functions. The formulas presented are: 1) \( \sin(\alpha)\cos(\beta) = \frac{1}{2}[\cos(\alpha - \beta) - \cos(\alpha + \beta)] \), 2) \( \cos(\alpha)\cos(\beta) = \frac{1}{2}[\cos(\alpha - \beta) + \cos(\alpha + \beta)] \), 3) \( \sin(\alpha)\cos(\beta) = \frac{1}{2}[\sin(\alpha + \beta) + \sin(\alpha - \beta)] \), and 4) \( \cos(\alpha)\sin(\beta) = \frac{1}{2}[\sin(\alpha + \beta) - \sin(\alpha - \beta)] \). The paragraph also demonstrates how to apply these formulas to simplify expressions such as \( \sin(7x)\sin(4x) \) and \( \sin(9x)\cos(3x) \), providing step-by-step solutions.

05:00
🔍 Sum to Product Trigonometric Identities

This section covers the sum to product trigonometric identities, which are used to transform the sum or difference of trigonometric functions into a product form. The identities include: 1) \( \sin(\alpha) + \sin(\beta) = 2\sin\left(\frac{\alpha + \beta}{2}\right)\cos\left(\frac{\alpha - \beta}{2}\right) \), 2) \( \sin(\alpha) - \sin(\beta) = 2\sin\left(\frac{\alpha - \beta}{2}\right)\cos\left(\frac{\alpha + \beta}{2}\right) \), 3) \( \cos(\alpha) + \cos(\beta) = 2\cos\left(\frac{\alpha + \beta}{2}\right)\cos\left(\frac{\alpha - \beta}{2}\right) \), and 4) \( \cos(\alpha) - \cos(\beta) = -2\sin\left(\frac{\alpha + \beta}{2}\right)\sin\left(\frac{\alpha - \beta}{2}\right) \). Examples provided include simplifying \( \sin(8x) + \sin(3x) \) and \( \cos(11x) + \cos(3x) \) using these identities.

10:03
📉 Verifying Trigonometric Identity with Sum to Product

The final paragraph focuses on verifying a specific trigonometric identity using the sum to product formulas. The identity to be proven is \( \frac{\sin(x) + \sin(3x)}{\cos(x) + \cos(3x)} = \tan(2x) \). The explanation begins by applying the sum to product identities to both the numerator and the denominator separately. The process simplifies the expression to \( \frac{\sin(2x)}{\cos(2x)} \), which is equivalent to \( \tan(2x) \), thus successfully verifying the identity. This paragraph emphasizes the importance of memorizing these formulas for efficient problem-solving in trigonometry.

Mindmap
Keywords
💡Product to Sum Formulas
Product to sum formulas are trigonometric identities that express products of trigonometric functions as sums or differences. In the video, these formulas are used to simplify expressions involving sine and cosine functions. For example, the script introduces the formula for sine alpha times cosine beta, which is shown to equal one-half times the difference and sum of cosine alpha minus beta and cosine alpha plus beta.
💡Trigonometric Expressions
Trigonometric expressions are mathematical expressions that involve trigonometric functions like sine, cosine, and tangent. The video's theme revolves around simplifying these expressions using product to sum and sum to product formulas. An example from the script is simplifying sine 7x times sine 4x using the product to sum formula.
💡Sine Function
The sine function is a fundamental trigonometric function that relates the ratio of the sides of a right triangle to the angle it is measured from. In the video, the sine function is used in various formulas and examples, such as sine alpha times sine beta, where alpha and beta represent angles.
💡Cosine Function
The cosine function is another basic trigonometric function that, like sine, relates to the sides of a right triangle and an angle. The video script uses cosine in multiple contexts, including in the product to sum formulas and simplifying expressions like sine 9x times cosine 3x.
💡Sum to Product Formulas
Sum to product formulas are trigonometric identities that convert sums of trigonometric functions into products. These are essential for simplifying expressions, as demonstrated in the video. For instance, the script explains how to use the sum to product formula to simplify sine 8x plus sine 3x into a product of sine and cosine functions.
💡Angles
Angles are a key concept in trigonometry and are used to define the input for trigonometric functions. In the video, angles are represented by variables such as alpha and beta, which are used in formulas to simplify trigonometric expressions. The script mentions angles in the context of simplifying expressions like sine 7x times sine 4x, where 7x and 4x are the angles.
💡Simplification
Simplification in the context of the video refers to the process of reducing complex trigonometric expressions into simpler forms using identities. The video provides several examples of simplifying expressions such as sine 7x times sine 4x to one-half cosine 3x minus cosine 11x, demonstrating the application of product to sum and sum to product formulas.
💡Tangent Function
The tangent function is the ratio of the sine to the cosine of an angle and is used in various trigonometric identities. In the video, tangent is used in the verification of an identity, where sine x plus sine 3x divided by cosine x plus cosine 3x is shown to be equal to tangent 2x.
💡Verification of Identity
Verification of identity in trigonometry involves proving that two expressions are equivalent using trigonometric identities. The video script includes an example of verifying the identity that the sum of sine x and sine 3x over the sum of cosine x and cosine 3x equals tangent 2x, showcasing the application of sum to product formulas.
💡Trigonometric Identities
Trigonometric identities are equations that hold true for all values of the variables involved and are used to simplify and manipulate trigonometric expressions. The video's main theme is based on these identities, particularly product to sum and sum to product formulas, which are used to simplify various expressions involving sine and cosine.
Highlights

Introduction to product-to-sum formulas in trigonometry.

First formula: sine alpha * cosine beta = 1/2 * (cosine (alpha - beta) - cosine (alpha + beta)).

Second formula: cosine alpha * cosine beta = 1/2 * (cosine (alpha - beta) + cosine (alpha + beta)).

Third formula: sine alpha * cosine beta = 1/2 * (sine (alpha + beta) + sine (alpha - beta)).

Fourth formula: cosine alpha * sine beta = 1/2 * (sine (alpha + beta) - sine (alpha - beta)).

Application of product-to-sum formulas to simplify trigonometric expressions.

Example: Simplifying sine 7x * sine 4x using product-to-sum formulas.

Result: sine 7x * sine 4x = 1/2 * (cosine 3x - cosine 11x).

Example: Simplifying sine 9x * cosine 3x using product-to-sum formulas.

Result: sine 9x * cosine 3x = 1/2 * (sine 12x + sine 6x).

Introduction to sum-to-product formulas.

First sum-to-product formula: sine alpha + sine beta = 2 * sine ((alpha + beta) / 2) * cosine ((alpha - beta) / 2).

Second sum-to-product formula: sine alpha - sine beta = 2 * sine ((alpha - beta) / 2) * cosine ((alpha + beta) / 2).

Third sum-to-product formula: cosine alpha + cosine beta = 2 * cosine ((alpha + beta) / 2) * cosine ((alpha - beta) / 2).

Fourth sum-to-product formula: cosine alpha - cosine beta = -2 * sine ((alpha + beta) / 2) * sine ((alpha - beta) / 2).

Example: Simplifying sine 8x + sine 3x using sum-to-product formulas.

Result: sine 8x + sine 3x = 2 * sine 11x * cosine 5x / 2.

Example: Simplifying cosine 11x + cosine 3x using sum-to-product formulas.

Result: cosine 11x + cosine 3x = 2 * cosine 14x * cosine 8x / 2.

Example: Simplifying sine 75 + sine 15 degrees using sum-to-product formulas.

Result: Exact value of sine 75 + sine 15 degrees using trigonometric values.

Verification of an identity: sine x + sine 3x / (cosine x + cosine 3x) = tangent 2x.

Explanation of how to use sum-to-product formulas to prove the identity.

Final verification of the identity using trigonometric identities.

Transcripts

Browse More Related Video

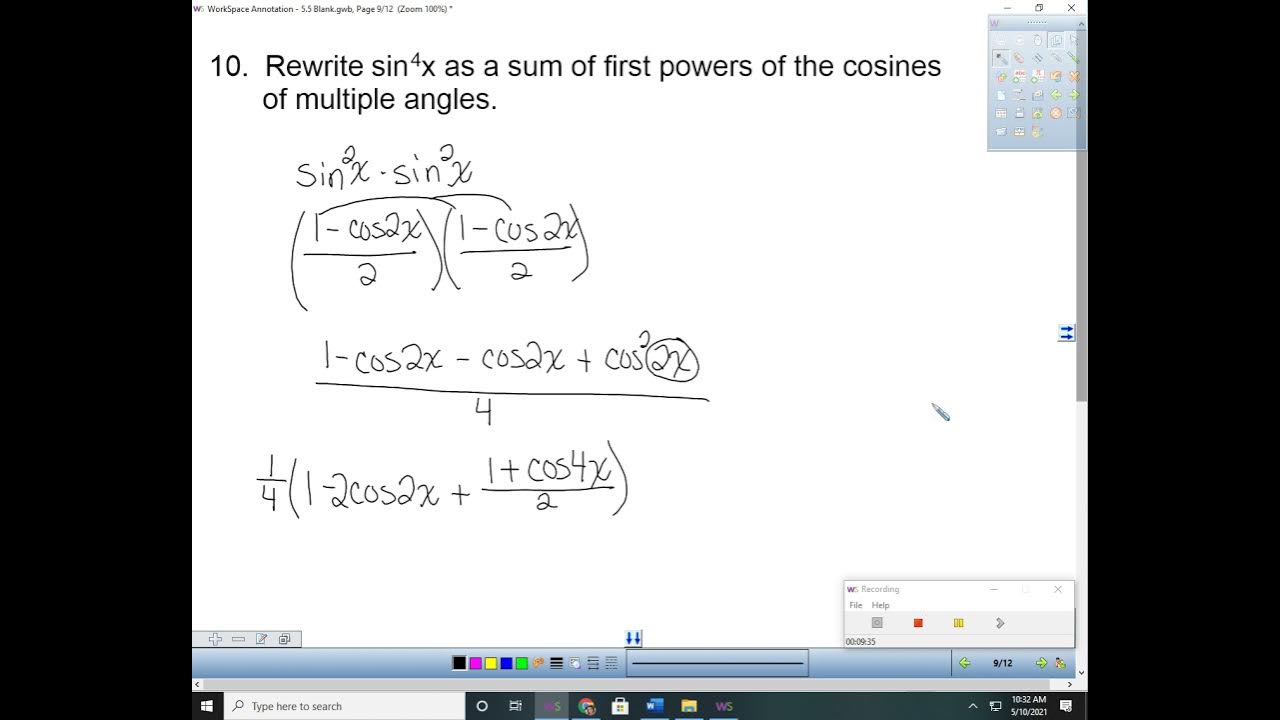
5.5 Multiple Angle and Product to Sum Formulas (Part 2)

Trig Integral Practice | MIT 18.01SC Single Variable Calculus, Fall 2010

Lec 3 | MIT 18.01 Single Variable Calculus, Fall 2007

Simplifying Trigonometric Expressions Using Power Reducing Formulas

Integral of sinx cosx

Ultimate trig identity problem study guide!

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
TrigonometryProduct-SumSimplificationEducationalFormulasTrig IdentitiesMathematicsScript ReviewSine CosineProblem Solving