Simplifying Trigonometric Expressions Using Power Reducing Formulas

The Organic Chemistry Tutor
19 Oct 201710:04
EducationalLearning
32 Likes 10 Comments

TLDRThis video script delves into the derivation and application of power reducing formulas in trigonometry. It begins by presenting the double angle formula for cosine and transforming it into a power reducing formula for sine squared. Similar steps are taken for cosine squared and tangent squared, leading to three key formulas. The script then demonstrates how to simplify complex trigonometric expressions, such as 4 sine squared x cosine squared x, and 16 sine to the fourth x, by applying these formulas. The process involves isolating terms, using foiling techniques, and strategically applying power reducing formulas to achieve simplified expressions with sine and cosine exponents equal to one.

Takeaways
  • 📚 The script discusses the derivation of power reducing formulas for trigonometric functions.
  • 🔍 It starts with the double angle formula for cosine, which is \( \cos(2\theta) = 1 - 2\sin^2(\theta) \).
  • 📐 From this, the power reducing formula for \( \sin^2(\theta) \) is derived as \( \sin^2(\theta) = \frac{1 - \cos(2\theta)}{2} \).
  • 📉 Another double angle formula for cosine is presented as \( 2\cos^2(\theta) - 1 = \cos(2\theta) \).
  • 📈 The power reducing formula for \( \cos^2(\theta) \) is derived as \( \cos^2(\theta) = \frac{1 + \cos(2\theta)}{2} \).
  • 📝 The script then moves on to derive the power reducing formula for \( \tan^2(\theta) \), resulting in \( \tan^2(\theta) = \frac{1 - \cos(2\theta)}{1 + \cos(2\theta)} \).
  • 🧩 An example is given to simplify the expression \( 4\sin^2(x)\cos^2(x) \) using the power reducing formulas.
  • 🔢 The simplified result of the expression is \( \frac{1 - \cos^2(4x)}{2} \), which further simplifies to \( \frac{1 - \cos(4x)}{2} \).
  • 📉 Another example is provided to reduce \( 16\sin^4(x) \) using the power reducing formula for \( \sin^2(x) \).
  • 📊 The final result for \( 16\sin^4(x) \) is \( 2\cos(4x) - 8\cos(2x) + 6 \).
  • 📝 The script emphasizes the importance of understanding and applying power reducing formulas to simplify trigonometric expressions.
Q & A

  • What is the double angle formula for cosine in terms of sine squared?

    -The double angle formula for cosine in terms of sine squared is given by \( \cos(2\theta) = 1 - 2\sin^2(\theta) \).

  • How do you derive the power reducing formula for sine squared from the double angle formula for cosine?

    -To derive the power reducing formula for sine squared, isolate \( \sin^2(\theta) \) in the double angle formula by subtracting 1 from both sides and then dividing by 2, resulting in \( \sin^2(\theta) = \frac{1 - \cos(2\theta)}{2} \).

  • What is the power reducing formula for cosine squared?

    -The power reducing formula for cosine squared is \( \cos^2(\theta) = \frac{1 + \cos(2\theta)}{2} \).

  • How can you express tangent squared in terms of cosine using the power reducing formulas?

    -Tangent squared can be expressed as \( \tan^2(\theta) = \frac{\sin^2(\theta)}{\cos^2(\theta)} \), which can be rewritten using the power reducing formulas for sine and cosine squared as \( \tan^2(\theta) = \frac{1 - \cos(2\theta)}{1 + \cos(2\theta)} \).

  • What is the expression for 4 sine squared x cosine squared x in terms of cosine using power reducing formulas?

    -The expression can be simplified to \( \frac{1 - \cos(4x)}{2} \) by using the power reducing formulas for sine squared and cosine squared and then foiling the resulting expression.

  • How does the power reducing formula for cosine squared change when the angle is doubled?

    -When the angle is doubled from \( x \) to \( 2x \), the power reducing formula for cosine squared becomes \( \cos^2(2x) = \frac{1 + \cos(4x)}{2} \).

  • What is the simplified result of the expression 4 sine squared x cosine squared x after applying the power reducing formulas?

    -The simplified result is \( \frac{1}{2} - \frac{1}{2}\cos(4x) \), which can be further factored to \( \frac{1}{2}(1 - \cos(4x)) \).

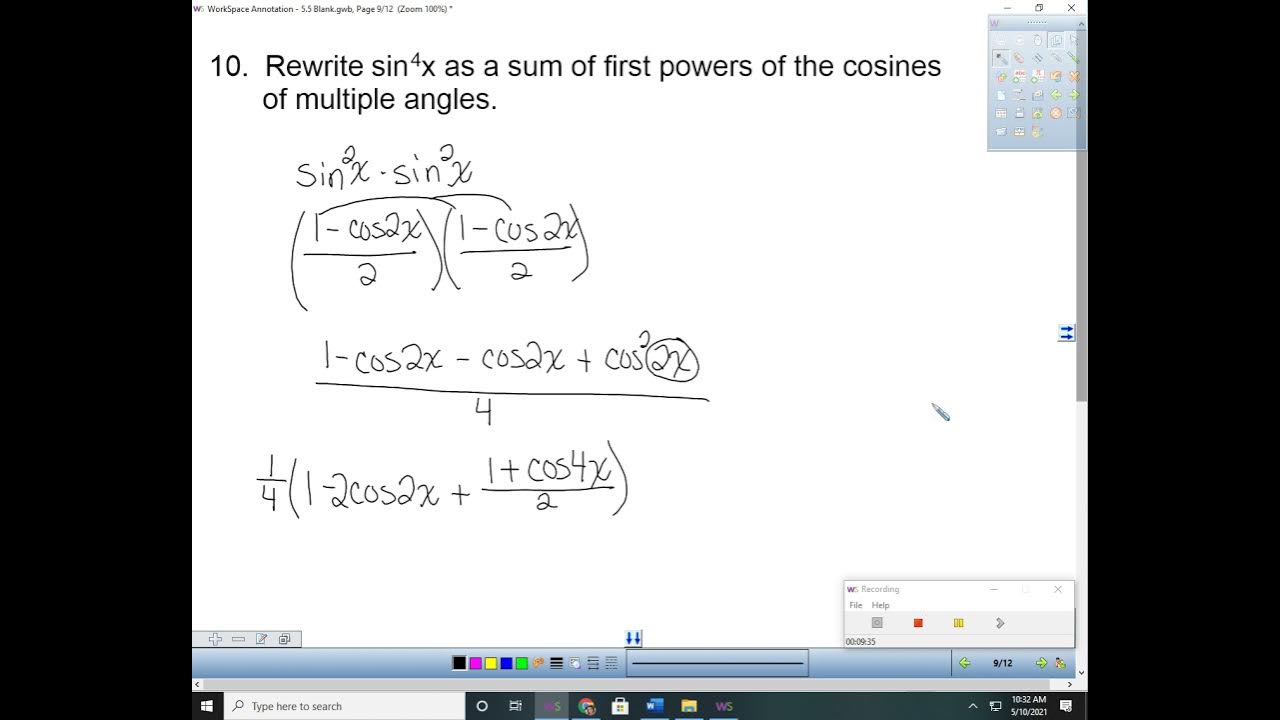
  • How can you rewrite sine to the fourth power as a product of sine squared?

    -Sine to the fourth power can be rewritten as \( (\sin^2(x))^2 \).

  • What is the final simplified form of 16 sine to the fourth x using power reducing formulas?

    -The final simplified form is \( 6 - 8\cos(2x) + 2\cos(4x) \).

  • What is the process of simplifying the expression 16 sine to the fourth x using power reducing formulas?

    -The process involves rewriting sine to the fourth as sine squared squared, applying the power reducing formula for sine squared, foiling the resulting expression, and then simplifying using the power reducing formula for cosine squared with a doubled angle.

Outlines
00:00
📚 Power Reducing Formulas for Trigonometry

This paragraph introduces the concept of power reducing formulas in trigonometry, specifically focusing on the derivation and application of these formulas for sine squared and cosine squared. The double angle formula for cosine is presented, leading to the isolation of sine squared and the derivation of its power reducing formula, which is sine squared equals one minus cosine of two theta divided by two. Similarly, the power reducing formula for cosine squared is derived from the double angle formula, resulting in one plus cosine of two theta divided by two. The paragraph also covers the derivation of the power reducing formula for tangent squared, which is one minus cosine of two theta divided by one plus cosine of two theta. An example is provided to demonstrate the simplification of the trigonometric expression four sine squared x cosine squared x using these formulas.

05:02
🔍 Simplifying Trigonometric Expressions Using Power Reducing Formulas

The second paragraph continues the discussion on power reducing formulas, illustrating how to simplify complex trigonometric expressions. It begins with the expression four sine squared x cosine squared x and shows the step-by-step process of using power reducing formulas to simplify it to one half minus one half cosine of four x. The paragraph then moves on to another example, demonstrating the reduction of 16 sine to the fourth x. The process involves rewriting sine to the fourth as sine squared squared and applying the power reducing formula for sine squared, leading to a final simplified expression of 2 cosine of four x minus 8 cosine of two x plus 6. This example showcases the practical application of power reducing formulas in simplifying higher power trigonometric expressions.

Mindmap
Keywords
💡Power Reducing Formulas
Power reducing formulas are mathematical identities used in trigonometry to simplify expressions involving trigonometric functions with exponents greater than one. In the context of the video, these formulas are derived from the double angle formulas and are used to express trigonometric functions with exponents in terms of those without exponents, making calculations more manageable. The script derives the power reducing formulas for sine squared and cosine squared, which are essential for simplifying complex trigonometric expressions.
💡Cosine Double Angle Formula
The cosine double angle formula is a trigonometric identity that expresses the cosine of twice an angle in terms of the cosine of the original angle. Specifically, the formula cos(2θ) = 1 - 2sin^2(θ) is used in the script to derive the power reducing formula for sine squared. It is a fundamental concept in the video's exploration of trigonometric identities and simplification techniques.
💡Sine Squared
Sine squared, represented as sin^2(θ), is a trigonometric function that involves squaring the sine of an angle. In the video, the power reducing formula for sine squared is derived as sin^2(θ) = (1 - cos(2θ))/2. This formula is crucial for simplifying expressions that include sine squared, as it allows for the conversion of the squared term into a form involving cosine, which can be more straightforward to work with.
💡Cosine Squared
Cosine squared, denoted as cos^2(θ), is similar to sine squared but applies to the cosine function. The video derives its power reducing formula as cos^2(θ) = (1 + cos(2θ))/2. This concept is integral to the video's theme of simplifying trigonometric expressions and is used alongside sine squared in various examples to demonstrate the application of power reducing formulas.
💡Tangent Squared
Tangent squared, written as tan^2(θ), is the square of the tangent function. In the script, the power reducing formula for tangent squared is derived from the formulas for sine and cosine squared, resulting in tan^2(θ) = (1 - cos(2θ))/(1 + cos(2θ)). This formula is part of the broader discussion on power reducing and is used to simplify expressions involving the tangent function.
💡Simplification
Simplification in the context of the video refers to the process of reducing complex trigonometric expressions to a simpler form using power reducing formulas. The script demonstrates this by simplifying expressions like 4sin^2(x)cos^2(x) into forms that only involve the first power of sine and cosine. Simplification is a key technique discussed in the video for managing and solving trigonometric problems.
💡Foil Method
The foil method is a technique used for multiplying two binomials. In the video, it is applied to expressions derived from power reducing formulas, such as (1 - cos(2x))(1 + cos(2x)). The script uses this method to expand and simplify expressions, which is an essential step in demonstrating the simplification of trigonometric identities.
💡Combining Like Terms
Combining like terms is a mathematical process where terms with the same variables and exponents are added or subtracted from each other to simplify an expression. In the video, this process is used after applying the foil method to expressions like 1 - cos^2(2x), resulting in a simplified form that is easier to work with.
💡Double Angle
The concept of double angle in the video refers to the process of doubling the angle in a trigonometric function, such as from θ to 2θ or from 2x to 4x. This is used in deriving and applying power reducing formulas, as well as in simplifying expressions by converting them into forms that are more manageable.
💡Sine to the Fourth
Sine to the fourth, or sin^4(x), is an example of a trigonometric function raised to a power greater than one. In the video, the power reducing formula for sine squared is applied twice to simplify sin^4(x) into an expression involving only the first power of sine and cosine. This demonstrates the power of these formulas in reducing the complexity of trigonometric expressions.
Highlights

Introduction to power reducing formulas and their derivation.

Derivation of the power reducing formula for sine squared using the double angle formula for cosine.

Isolating sine squared to get the power reducing formula: sine squared equals one minus cosine two theta divided by two.

Derivation of the power reducing formula for cosine squared using the double angle formula.

Isolating cosine squared to get the power reducing formula: cosine squared equals one plus cosine two theta divided by two.

Introduction to deriving the power reducing formula for tangent squared.

Expression of tangent squared in terms of sine and cosine squared.

Derivation of the power reducing formula for tangent squared: one minus cosine two theta divided by one plus cosine two theta.

Explanation of how to simplify the expression 4 sine squared x cosine squared x using power reducing formulas.

Application of sine squared and cosine squared power reducing formulas to simplify the expression.

Simplification of the expression to half minus half cosine four x.

Introduction to reducing 16 sine to the fourth x using power reducing formulas.

Rewriting sine to the fourth as sine squared squared and applying the power reducing formula.

Foil method application to expand and simplify the expression.

Final simplification of the expression to 2 cosine 4x minus 8 cosine 2x plus 6.

Emphasis on writing down all three power reducing formulas for sine squared, cosine squared, and tangent squared.

Transcripts

Browse More Related Video

Integral of sinx cosx

Reduction Formulas For Integration

Half Angle Formulas & Identities - Evaluating Trigonometric Expressions

5.5 Multiple Angle and Product to Sum Formulas (Part 2)

Formulas for Trigonometric Functions: Sum/Difference, Double/Half-Angle, Prod-to-Sum/Sum-to-Prod

Inverse Trig Functions With Double Angle Formulas and Half Angle Identities - Trigonometry

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
TrigonometryDouble AnglePower ReducingSine SquaredCosine SquaredTangent SquaredDerivationFormulasMathematicsEducational