5.5 Multiple Angle and Product to Sum Formulas (Part 2)

MathDramaQueen

10 May 202124:15

EducationalLearning

32 Likes 10 Comments

TLDRThe video script discusses trigonometric identities, focusing on deriving multiple angle formulas, power reducing formulas, and half angle formulas. It demonstrates the process of simplifying trigonometric expressions using these identities, such as converting sine of 3x into a form involving sine and cosine of 2x, and verifying the results. The script also covers calculating sine, cosine, and tangent of specific angles using half angle formulas.

Takeaways

🔢 The script discusses deriving a multiple angle formula for sine of 3x by considering it as sine of 2x plus x.
📚 The double angle formula for sine is used, which is sine 2x = 2 sin x cos x.
🔍 The sum formula is applied to split sine of 3x into sine of 2x cos x + cos of 2x sin x.
📈 The script simplifies the expression by breaking down cosine 2x into 1 - 2 sin^2 x and multiplying it by sin x.
🧩 The Pythagorean identity sin^2 x + cos^2 x = 1 is used to further simplify the expression to all sine terms.
🔄 The script verifies the derived formula by comparing it to the double angle identity for cosine squared theta - sin^2 theta.
📉 Power reducing formulas are introduced to rewrite trigonometric functions in terms of cosine of multiple angles.
🔗 The process involves simplifying expressions to have all powers of one and all cosines, which is achieved by power reducing sine^4 x and cosine^4 x.
📌 Half angle formulas are discussed, explaining how to find sine and cosine of an angle when only half the angle is given.
📐 The script provides examples of using half angle formulas to find sine, cosine, and tangent of specific angles like 105° and 165°.
⚖️ The importance of identifying the quadrant of the angle is highlighted to determine the correct sign of the sine and cosine values.

Q & A

What is the purpose of deriving the multiple angle formula for sine of 3x?
-The purpose is to express sine of 3x in terms of sine and cosine of 2x and x, using sum and double angle formulas, which simplifies the expression and makes it easier to work with in trigonometric calculations.
How is sine of 3x represented in the script?
-Sine of 3x is represented as sine of (2x + x), which allows the use of sum and double angle formulas to break it down into more manageable components.
What is the double angle formula used for sine in the script?
-The double angle formula used is sine 2x = 2 * sine x * cosine x, which helps in breaking down the expression for sine of 3x.
Why was the formula 1 - 2 * sine squared theta chosen for cosine 2x in the script?
-This formula was chosen because it helps in simplifying the expression by converting all terms into sine functions, making it easier to combine like terms and simplify the overall expression.
What is the Pythagorean identity used in the script to simplify cosine squared x?
-The Pythagorean identity used is 1 - sine squared x = cosine squared x, which is used to replace cosine squared x in the expression to further simplify it.
How does the script verify the derived formula for sine of 3x?
-The script verifies the formula by comparing it to the double angle identity cosine squared theta - sine squared theta and showing that the derived expression matches this identity when the angle is doubled.
What are power reducing formulas and how are they used in the script?
-Power reducing formulas are used to express higher powers of sine, cosine, or tangent in terms of 1 and cosine. In the script, they are used to rewrite sine to the fourth and cosine to the fourth as expressions involving cosine squared and cosine to simplify the calculations.
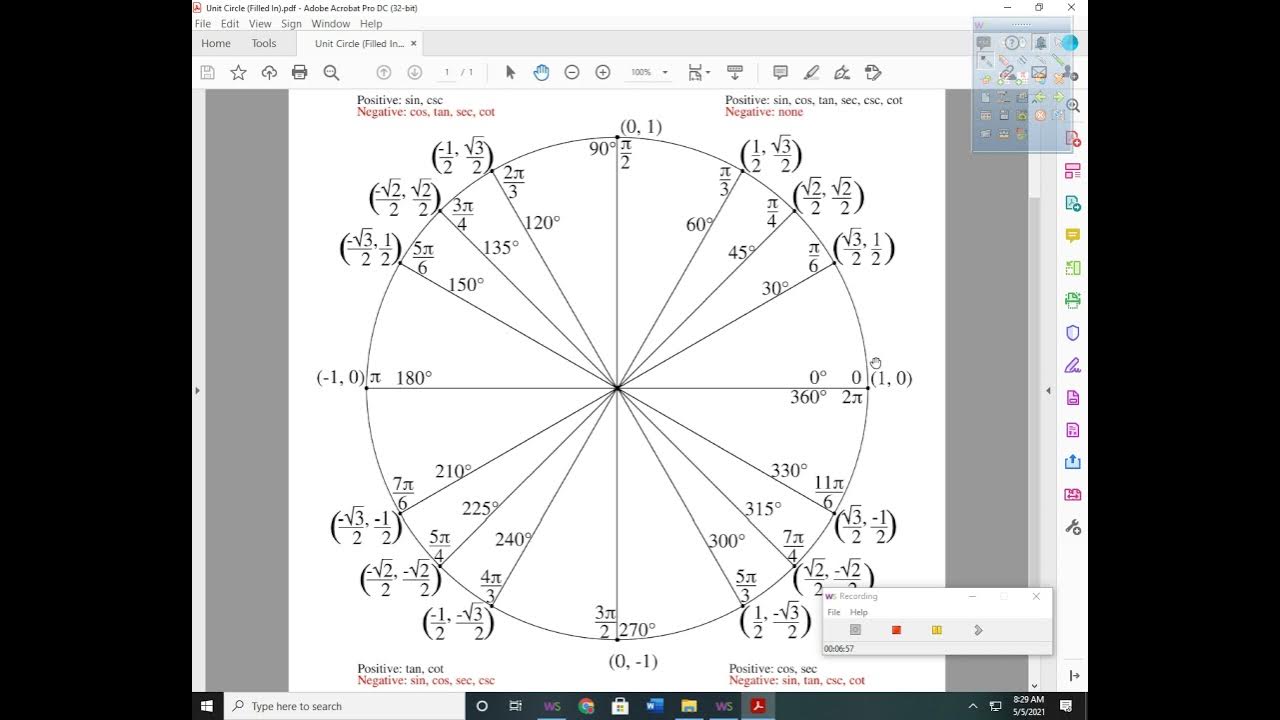
How is the half angle formula used in the script for sine of 105 degrees?
-The half angle formula is used by first identifying the quadrant of the angle (quadrant 2), then doubling the angle to 210 degrees, and using the formula sine u/2 = sqrt(1 - cosine u) to find the sine of 105 degrees.
What is the process for finding the sine, cosine, and tangent of 165 degrees as described in the script?
-The process involves identifying the quadrant (quadrant 2), doubling the angle to 330 degrees, and using the half angle formulas to find the sine, cosine, and tangent of 165 degrees. The cosine and tangent values are calculated using the cosine and sine values of 330 degrees.
Why is it important to consider the quadrant when using half angle formulas?
-Considering the quadrant is important because it determines the sign of the sine and cosine values. This is crucial for correctly applying the half angle formulas and obtaining the right results for angles in different quadrants.

Outlines

00:00

📚 Derivation of the Sine of Triple Angle Formula

The paragraph begins with the derivation of the sine of a triple angle formula, specifically sine of 3x. The instructor starts by expressing sine of 3x as the sum of sine of 2x and x, then applies the sum formula for sine to break it down into sine of 2x times cosine of x plus cosine of 2x times sine of x. Using the double angle formula for sine, this is further simplified to 2 sine x times cosine x. The cosine of 2x is then expanded using the identity 1 - 2 sine squared x. The instructor simplifies the expression by combining like terms and eventually verifies the result against the double angle identity for cosine squared theta minus sine squared theta, adjusting the formula to match the angle 2a, which represents the angle before it was doubled.

05:03

🔍 Power Reducing Formulas and Simplification

This paragraph delves into the process of simplifying trigonometric expressions using power reducing formulas. The instructor discusses the challenge of simplifying sine to the fourth and cosine to the fourth of x, and how to rewrite them using the difference of squares. The Pythagorean identity is applied to further simplify the expressions, leading to a form that only includes cosine to the first power. The power reducing formulas are then introduced, which allow for the simplification of sine squared, cosine squared, and tangent squared to expressions involving cosine of double angles. The instructor demonstrates the application of these formulas to rewrite sine to the fourth of x as a combination of cosine terms, ultimately aiming for an expression with all cosines to the first power.

10:05

📉 Advanced Trigonometric Simplification and Verification

The instructor continues with advanced trigonometric simplification, focusing on expressing trigonometric functions in terms of cosine and reducing powers. The paragraph covers the process of simplifying expressions involving sine and cosine to the fourth power, using power reducing formulas and the Pythagorean identity. The goal is to rewrite the expressions in a form that only includes cosine terms with the first power. The instructor also demonstrates the verification of the derived formulas, ensuring that the left-hand side of the equation matches the right-hand side, thus confirming the accuracy of the simplification process.

15:06

📐 Half-Angle Formulas and Their Application

This paragraph introduces half-angle formulas and their application in trigonometry. The instructor explains how to use these formulas to find the sine, cosine, and tangent of an angle that has been halved. The process involves identifying the quadrant in which the angle lies, which is crucial for determining the sign of the result. The instructor provides an example using the sine of 105 degrees, showing how to double the angle for the formula and then apply the half-angle formula to find the sine value. The cosine of 210 degrees is calculated, and the result is simplified to provide the final answer.

20:08

📘 Calculation of Trigonometric Functions for Specific Angles

The final paragraph covers the calculation of sine, cosine, and tangent for the specific angle of 165 degrees. The instructor first determines the quadrant of the angle to ascertain the signs of the trigonometric functions. Using the half-angle formulas, the instructor calculates the sine and cosine of 165 degrees, doubling the angle to 330 degrees for the formula. The cosine of 330 degrees is found using the unit circle, and the results are simplified. The tangent of 165 degrees is also calculated using a half-angle formula, resulting in a negative value. The instructor corrects a previous mistake regarding the cosine value for an angle, ensuring the accuracy of the calculations.

Mindmap

Keywords

💡Multiple Angle Formula

A multiple angle formula is a mathematical expression used to express the trigonometric functions of a multiple of an angle in terms of the trigonometric functions of the original angle. In the video, the derivation of the sine of 3x is an example of using multiple angle formulas, where sine of 3x is expressed as the sum of sine of 2x and cosine x, which is then further broken down using double angle identities.

💡Double Angle Identity

A double angle identity is a specific type of multiple angle formula that expresses trigonometric functions of twice an angle in terms of the functions of the original angle. In the script, the double angle identities for sine and cosine are used to simplify expressions like sine(2x) and cosine(2x), which are then used to derive the formula for sine(3x).

💡Sum Formula

The sum formula is a trigonometric identity that allows the expression of the sine of the sum of two angles in terms of the sines and cosines of the individual angles. In the video, the sum formula is applied to the expression sine(2x + x) to break it down into sine(2x) and cosine(x), which is the first step in deriving the sine of 3x.

💡Pythagorean Identity

The Pythagorean identity is a fundamental trigonometric identity stating that the square of sine plus the square of cosine of an angle is equal to one: sin^2(x) + cos^2(x) = 1. In the script, this identity is used to simplify expressions involving cosine squared x, helping to reduce the complexity of the derived formulas.

💡Power Reducing Formula

A power reducing formula is used to express higher powers of trigonometric functions in terms of first power functions, typically involving the use of double angle formulas. In the video, power reducing formulas are applied to expressions like sine^4(x) to rewrite them in a form that involves only first power trigonometric functions, simplifying the expressions.

💡Half Angle Formula

A half angle formula is a trigonometric identity that expresses the sine, cosine, or tangent of half an angle in terms of the sine and cosine of the full angle. In the script, the half angle formulas are used to find the values of sine, cosine, and tangent for specific angles by considering half of those angles and then adjusting for the correct quadrant.

💡Trigonometric Functions

Trigonometric functions are mathematical functions of an angle, including sine, cosine, and tangent, which have various applications in mathematics, physics, and engineering. The video focuses on deriving and simplifying expressions involving these functions, particularly in the context of multiple and half angles.

💡Sine Function

The sine function is one of the primary trigonometric functions, representing the ratio of the length of the side opposite an angle to the length of the hypotenuse in a right-angled triangle. In the video, the sine function is the subject of the derivation for sine(3x) and is also used in the context of half angle formulas.

💡Cosine Function

The cosine function is another fundamental trigonometric function, representing the ratio of the adjacent side to the hypotenuse in a right-angled triangle. The video script involves the cosine function in the derivation of multiple angle formulas and in the simplification of expressions using power reducing formulas.

💡Tangent Function

The tangent function is the ratio of the sine to the cosine of an angle, and it is used in various trigonometric identities and calculations. In the script, the tangent function is calculated for specific angles using half angle formulas, demonstrating its application in solving trigonometric problems.

💡Quadrant

In the context of the unit circle and trigonometry, a quadrant refers to one of the four equal divisions of the circle by the x and y axes. The quadrant is important for determining the signs of trigonometric functions, as the sign of sine, cosine, and tangent changes depending on the quadrant in which the angle lies. In the script, the quadrant is used to determine the correct sign for half angle formulas.

Highlights

Deriving a multiple angle formula for sine of 3x by considering it as sine of 2x plus 1x.

Using sum formula to split sine of 3x into sine of 2x and cosine of x.

Applying double angle formula to break down sine 2x into 2 sine x cosine x.

Choosing the double angle formula 1 - 2 sine squared theta to simplify expressions to all sines.

Simplifying the expression to combine like terms and achieve a form similar to the double angle identity.

Verifying the derived formula by comparing it to the double angle identity for cosine squared theta - sine squared theta.

Factoring the difference of squares to simplify expressions involving cosine to the fourth.

Using Pythagorean identity to replace terms and simplify further.

Introducing power reducing formulas for sine squared, cosine squared, and tangent squared.

Rewriting sine to the fourth as sine squared x times sine squared x and applying power reducing formulas.

Simplifying expressions by multiplying and combining terms over a common denominator.

Discussing the process of power reducing cosine squared to x by doubling the angle.

Describing the process of power reducing cosine to the fourth by viewing it as cosine squared x times cosine squared x.

Introducing half angle formulas for sine and cosine and explaining their application based on quadrant.

Calculating sine of 105 using the half angle formula and verifying the quadrant to determine the sign of the root.

Calculating cosine of 165 using the half angle formula and adjusting for the negative root in quadrant two.

Calculating tangent of 165 using the half angle formula and simplifying the expression.

Correcting a mistake in the calculation of cosine for a specific angle by adjusting the sign based on the quadrant.

Transcripts

Browse More Related Video

How to Use the Double and Half Angle Formulas for Trigonometry (Precalculus - Trigonometry 28)

Proving the Double and Half Angle Formulas for Trigonometry (Precalculus - Trigonometry 27)

5.5 Multiple Angle and Product to Sum Formulas (Part 1)

Half Angle Formulas & Identities - Evaluating Trigonometric Expressions

Product To Sum Identities and Sum To Product Formulas - Trigonometry

Verifying Trigonometric Identities With Double Angle Formulas

Related Tags

Trigonometry Math Tutorial Double Angle Sine Formula Cosine Formula Power Reducing Half Angle Unit Circle Pythagorean Identity Trigonometric Functions