Lec 3 | MIT 18.01 Single Variable Calculus, Fall 2007
TLDRThis MIT OpenCourseWare lecture focuses on developing derivative formulas to differentiate trigonometric functions, specifically sine and cosine. The professor introduces specific and general derivative formulas, then delves into the process of differentiating sine and cosine using the difference quotient and sum formulas. Through geometric proofs, the professor demonstrates that the derivative of sine is cosine and the derivative of cosine is negative sine, highlighting the importance of understanding trigonometric identities and limits. The lecture also previews the product and quotient rules for differentiation, setting the stage for further exploration in subsequent classes.
Takeaways
- 📚 The lecture aims to develop derivative formulas, specifically focusing on trigonometric functions, aiming to differentiate everything.
- 🔢 Derivative formulas are divided into specific ones for particular functions like \( x^n \) or \( \frac{1}{x} \), and general ones applicable to combinations of functions, such as sum and product rules.
- 📉 The lecture begins with the differentiation of sine and cosine functions, using the difference quotient and the sum formula for sine to find the derivative of sine.
- 📈 The process involves simplifying the expression for the derivative using trigonometric identities and taking limits as \( \Delta x \) approaches 0, resulting in the derivative of sine being cosine.
- 🔍 The importance of correctly applying trigonometric identities and simplifying expressions is emphasized to avoid confusion and errors in differentiation.
- 📐 A geometric proof is provided for the derivative of sine, using the unit circle and the concept that short pieces of curves are nearly straight.
- 📘 The proof relies on the understanding of radians as the unit of angle measurement, which is crucial for the correctness of the formulas.
- 📌 The lecture introduces general differentiation rules, such as the product rule and the quotient rule, which are essential for differentiating more complex functions.
- 🔑 The product rule states that the derivative of a product of two functions is the derivative of one times the other plus the other times the derivative of the first.
- 📘 The quotient rule provides a formula for the derivative of a quotient of two functions, which is \( (u'v - uv') / v^2 \), where \( v \) must not be zero.
- 📝 The lecture concludes with an emphasis on the importance of understanding and being able to apply these general rules for differentiation in various mathematical contexts.
Q & A
What is the main goal of the lecture?
-The main goal of the lecture is to develop several derivative formulas that will allow the differentiation of all functions, focusing on trigonometric functions such as sine and cosine.
What are the two types of derivative formulas mentioned in the lecture?
-The two types of derivative formulas mentioned are specific formulas, which give the derivative of a particular function like x^n or 1/x, and general formulas, which provide rules for combining derivatives, such as the sum and constant multiplication rules.
Why are both specific and general derivative formulas important?
-Both specific and general derivative formulas are important because they complement each other. Specific formulas provide the base cases, while general formulas allow for the derivation of more complex functions by applying operations like addition and multiplication.
What is the difference quotient used for?
-The difference quotient is used to calculate the derivative of a function. It involves taking the difference between the function values at two points and dividing by the difference in the x-values, then taking the limit as the x-values approach each other.
How does the sum formula for sine function help in finding the derivative of sine?
-The sum formula for sine, which is sin(a + b) = sin a cos b + cos a sin b, helps in finding the derivative of sine by allowing the simplification of the difference quotient for sin(x + delta x) - sin x divided by delta x.
What is the derivative of the sine function?
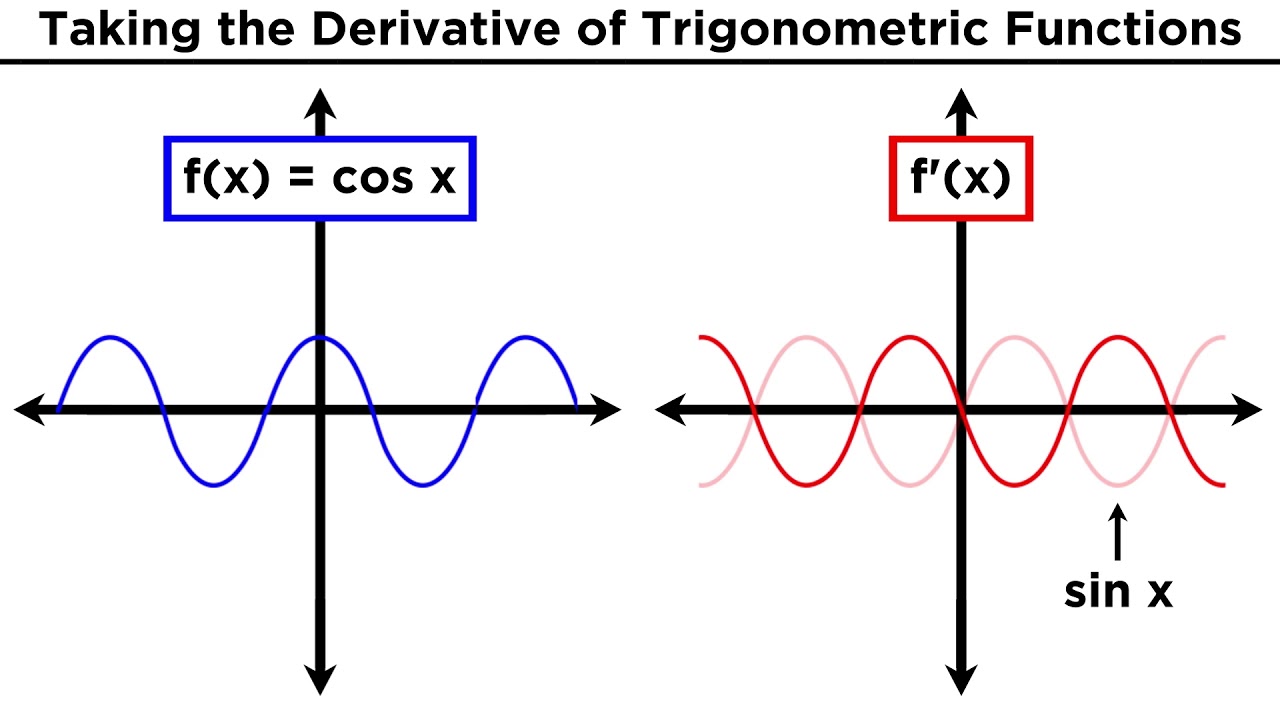
-The derivative of the sine function is the cosine function, which is denoted as d/dx sin x = cos x.
What are properties A and B mentioned in the lecture, and why are they important?
-Properties A and B are limit facts that are used in the proofs of the derivatives of sine and cosine functions. Property A is the limit as delta x tends to 0 of (cos delta x - 1) / delta x, which equals 0. Property B is the limit as delta x tends to 0 of (sin delta x) / (delta x), which equals 1. These properties are important because they simplify the process of finding derivatives and are used to establish the fundamental rules of differentiation.
How does the geometric proof of the derivative of sine function work?
-The geometric proof of the derivative of sine function involves considering a unit circle and a point moving along it. By analyzing the vertical displacement (change in y) as the point moves from angle theta to angle theta plus delta theta, and using the approximation that short pieces of curves are nearly straight, the proof shows that the rate of change of y (which is sin theta) with respect to theta is approximately cos theta, which becomes exact in the limit as delta theta approaches 0.
What are the product rule and quotient rule in differentiation?
-The product rule states that the derivative of the product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function. The quotient rule states that the derivative of the quotient of two functions u and v (where v is not zero) is given by (u'v - uv') / v^2.
Why are the product rule and quotient rule valuable in differentiation?
-The product rule and quotient rule are valuable in differentiation because they provide a systematic way to find the derivatives of more complex functions that are products or quotients of simpler functions. These rules are used frequently in calculus and are essential for solving a wide range of problems.
Outlines
📚 Introduction to Derivative Formulas and MIT OpenCourseWare
The paragraph introduces the purpose of the video, which is to develop more derivative formulas to achieve the goal of differentiating any function. It highlights the importance of specific and general derivative formulas, such as those for x^n, (1/x), and the rules for combining functions through addition and multiplication by a constant. The speaker, a professor, emphasizes the utility of these formulas for polynomials and other functions and mentions the focus on trigonometric functions, specifically sine and cosine derivatives, in this lecture. The video is part of MIT OpenCourseWare, a free educational resource supported by donations.
🔍 Deriving the Derivative of Sine Function Using Trigonometric Identities
The professor begins the derivation of the sine function's derivative by applying the difference quotient and the sum formula for sine. The process involves taking sin(x + delta x), subtracting sin(x), and dividing by delta x. The sum formula for sine, sin(a + b) = sin(a)cos(b) + cos(a)sin(b), is then used to simplify the expression. The goal is to simplify and group terms in a way that will allow the limit to be taken as delta x approaches zero, which is a crucial step in finding the derivative.
📉 Limit Process and Simplification for Sine Function Derivative
The paragraph delves into the limit process necessary to find the derivative of the sine function. The professor explains the need to group terms so that the limit can be taken without resulting in a 0/0 indeterminate form. By recognizing that cosine of zero is one, the terms are grouped and simplified to reveal that the derivative of sine with respect to x is cosine, as the limit of (sin(delta x) - sin(x)) / delta x approaches zero. This leads to the conclusion that the derivative of sine is cosine, simplified as cos(x).
📚 Derivative of Cosine Function and Proof Structure
The professor transitions to the derivative of the cosine function, using the sum rule for cosine to set up the difference quotient. The goal is to simplify the expression in a similar manner to the sine function's derivative, resulting in an expression involving cos(x)cos(delta x) - sin(x)sin(delta x). The paragraph also discusses the structure of the proofs for the derivatives of sine and cosine, highlighting that knowing the rate of change at x = 0 allows for determining the derivatives at all points.
📉 Geometric Proof for the Derivative of Cosine Function
The paragraph presents a geometric proof for the derivative of the cosine function. The proof involves drawing a unit circle and using geometric interpretations of the sine and cosine functions. The professor introduces the concept of replacing delta x with an angle theta and explains how the limit of (cos(theta) - 1) / theta tends to zero as theta approaches zero, which is a key step in proving the derivative of cosine.
📐 Geometric Interpretation of Sine and Cosine Derivatives
The professor provides a geometric interpretation of the derivatives of sine and cosine functions. The explanation involves visualizing the unit circle and the angles involved, with the aim of demonstrating how the derivatives are derived from the geometric properties of the circle. The emphasis is on the concept that short pieces of curves on the unit circle can be approximated as straight lines, which simplifies the calculation of derivatives.
🤔 Addressing Questions and Clarifying the Derivative Proofs
The paragraph involves a Q&A session where the professor addresses students' questions about the proofs for the derivatives of sine and cosine. Topics discussed include the interpretation of the limit as 0/0, the significance of radians in the geometric proofs, and the rationale behind the specific lengths used in the unit circle diagrams. The professor clarifies misconceptions and reinforces the importance of using the correct units for angles.
📚 General Differentiation Rules: Product and Quotient Rules
The final paragraph introduces general rules for differentiation that are applicable to a wide range of functions. The product rule states that the derivative of the product of two functions is the derivative of the first function times the second, plus the first function times the derivative of the second. The quotient rule provides a formula for the derivative of a quotient of two functions, which involves the product of the numerator's derivative and the denominator, minus the product of the numerator and the denominator's derivative, all divided by the square of the denominator. The professor emphasizes the utility of these rules in various calculus applications.
Mindmap
Keywords
💡Derivative
💡Trigonometric Functions
💡Difference Quotient
💡Sum Formula
💡Limit
💡Polynomials
💡Product Rule
💡Quotient Rule
💡Arc Length
💡Geometric Proof
Highlights
Introduction to derivative formulas, emphasizing both specific and general formulas for differentiation.
Explanation of specific derivative formulas for functions like x^n and 1/x.
Discussion of general derivative formulas, such as the sum and constant multiplication rules.
Importance of both specific and general formulas in differentiating polynomials and other functions.
Introduction of trigonometric functions, specifically focusing on the sine and cosine functions.
Derivation of the derivative formula for the sine function using the difference quotient and sum formula for sine.
Use of the common factor (sin x) and the limit process to simplify the derivative of sine to cosine.
Introduction of important limit facts labeled as A and B, which are crucial for the proofs.
Derivation of the derivative formula for the cosine function, highlighting the difference in the sum rule for cosine.
Explanation of how the rate of change of sine and cosine at x = 0 gives all values of their derivatives.
Geometric proof of property B using the unit circle and the concept of arc length.
Illustration of how short curves are nearly straight, a principle used in the geometric proof.
Proof of property A using a geometric interpretation involving the cosine function.
Discussion on the importance of using radians in the geometric proofs for the derivatives of sine and cosine.
Second geometric proof of the derivative of sine using the concept of a particle moving along a unit circle.
Introduction of general differentiation rules, including the product rule and quotient rule.
Emphasis on the importance of understanding and applying the product and quotient rules in differentiation.
Transcripts
Browse More Related Video

Product To Sum Identities and Sum To Product Formulas - Trigonometry

Quotient Rule | MIT 18.01SC Single Variable Calculus, Fall 2010
Derivatives of Trigonometric Functions

Derivative of Sine and Cosine Functions | Calculus

The derivative of Trigonometric Functions

Derivatives of Trig Functions - Calculus | MCV4U
5.0 / 5 (0 votes)
Thanks for rating: