How To Calculate The Missing Side Length of a Triangle

The Organic Chemistry Tutor

3 Jun 202029:56

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video offers a comprehensive guide on calculating missing side lengths of triangles using various methods. It begins with the Pythagorean theorem for right triangles, then progresses to trigonometric ratios like SOHCAHTOA for non-right triangles with given angles. The video also covers the law of sines and cosines for more complex scenarios, including composite triangles. Finally, it demonstrates solving triangles with multiple variables using geometric means and algebraic manipulation, providing a step-by-step approach to tackle different types of triangle problems.

Takeaways

📐 The video explains how to calculate the missing side length of a triangle using various methods, starting from easy examples to more complex ones.
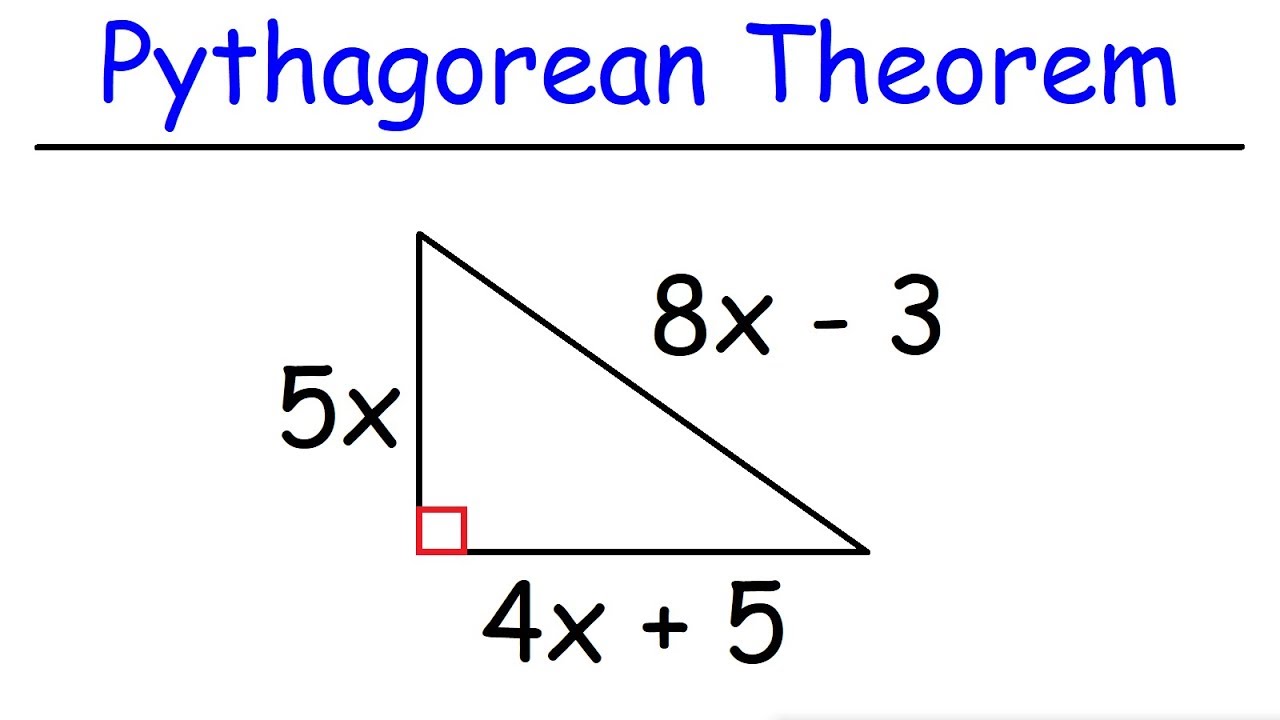
📝 The Pythagorean theorem is introduced and used for finding the missing side of right triangles, with a formula: a² + b² = c².
🔺 In right triangles, the hypotenuse (c) is the longest side, and the theorem is applied by substituting given side lengths and solving for the unknown side.
📏 Examples include solving for side lengths using specific values like 6, 10, and 16, demonstrating the steps to isolate and solve for the missing variable.
🧮 For non-perfect squares, the process of simplifying radicals is explained, such as finding a perfect square factor to simplify the square root.
🔍 Trigonometric ratios (sine, cosine, tangent) are used for triangles with given angles and sides, with a mnemonic 'SOHCAHTOA' to remember the ratios.
📊 Examples involving angles and sides show how to use sine, cosine, and tangent functions to find missing sides, including steps for calculation and cross-multiplication.
📐 The Law of Sines and the Law of Cosines are introduced for non-right triangles, providing formulas and examples to find missing side lengths.
📏 Composite triangle problems are solved by writing and solving multiple equations using trigonometric identities and algebraic manipulation.
📊 The concept of geometric mean is used to find missing side lengths in specific triangle configurations, demonstrating how to identify and apply the appropriate formulas.

Q & A

What is the Pythagorean theorem and how is it used in the context of the video?
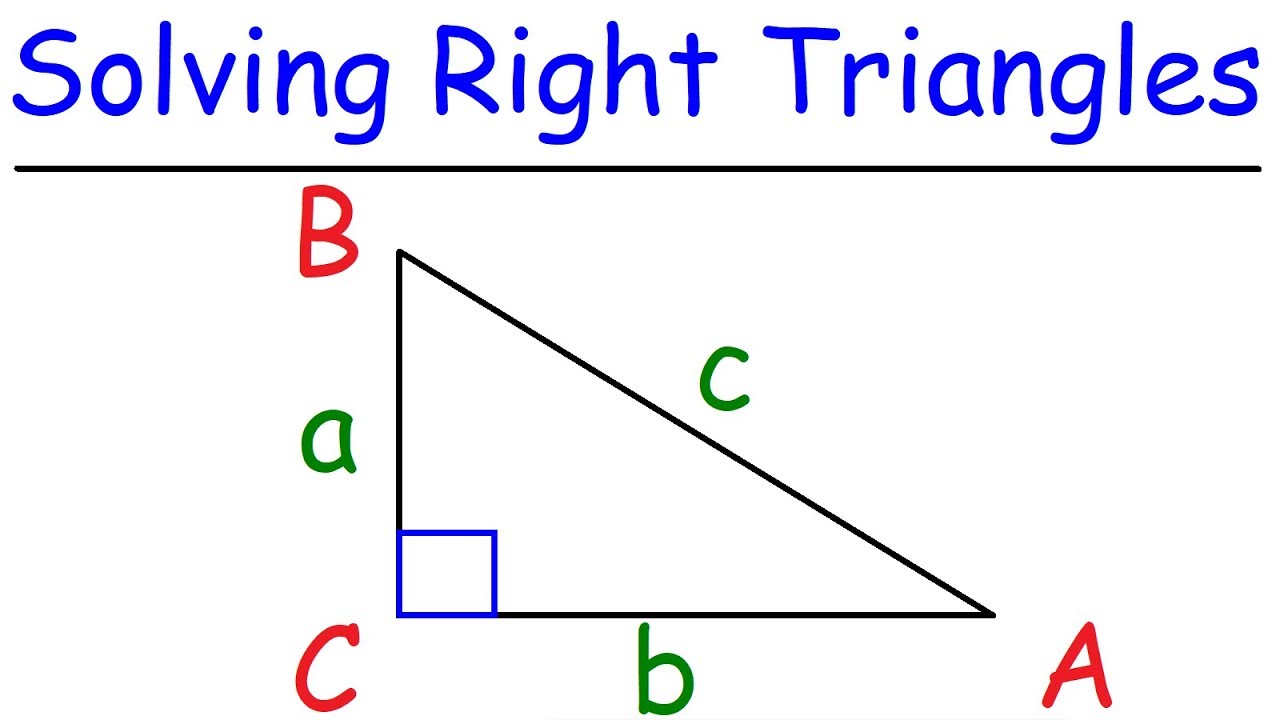
-The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. In the video, it is used to calculate the missing side of a right triangle when two sides are known.
How do you determine which side is the hypotenuse when applying the Pythagorean theorem?
-The hypotenuse is the longest side of a right triangle and is always opposite the right angle. In the video, it is mentioned that 'c' represents the hypotenuse, and it is identified as the longest side.
What is the process for solving a triangle when you know one angle and the hypotenuse but not the other sides?
-In this case, you can use trigonometric ratios such as sine, cosine, or tangent, which relate the angles of a right triangle to the ratios of its sides. The video demonstrates using the sine ratio to find the missing side when given the angle and the hypotenuse.
What is the SOHCAHTOA mnemonic used for in trigonometry?
-SOHCAHTOA is a mnemonic used to remember the trigonometric ratios for the angles in a right triangle: sine (opposite/hypotenuse), cosine (adjacent/hypotenuse), and tangent (opposite/adjacent). The video uses this mnemonic to solve for missing sides given an angle and a side.
How does the video handle a situation where the triangle is not a right triangle and you need to find a missing side?
-For non-right triangles, the video introduces the Law of Sines and the Law of Cosines. The Law of Sines relates the ratios of the sides to the sines of their opposite angles, while the Law of Cosines is used when you know two sides and the included angle to find the third side.
What is the Law of Sines and how is it applied in the video?
-The Law of Sines states that the ratio of a side of a triangle to the sine of its opposite angle is constant for all three sides and angles of the triangle. In the video, it is used to find a missing side when you have two angles and one side of a non-right triangle.
How is the Law of Cosines different from the Pythagorean theorem?
-The Law of Cosines is used for any triangle, not just right triangles, and it relates the lengths of all three sides to the cosine of one of the angles. The Pythagorean theorem is a specific case of the Law of Cosines that applies only to right triangles.
In the video, how are composite triangles handled when finding missing side lengths?
-Composite triangles are broken down into smaller right triangles, and trigonometric ratios or the Pythagorean theorem are applied to each smaller triangle to find the missing sides. The video demonstrates using tangent and then solving a system of equations to find the missing sides.
What is the geometric mean and how is it used in the video to find a missing side?
-The geometric mean of two numbers is the square root of their product. In the video, it is used to find the missing side 'x' when 'x' is the altitude to the hypotenuse in a triangle composed of three right triangles.
How does the video solve for multiple missing sides using the Pythagorean theorem?
-The video demonstrates creating multiple equations based on the Pythagorean theorem for each right triangle within a composite figure. By manipulating these equations, such as subtracting one from another, the video solves for the missing sides algebraically.

Outlines

00:00

📚 Introduction to Triangle Side Calculation

This paragraph introduces the topic of the video, which is calculating missing side lengths of triangles. It begins with a simple example of a right triangle where two sides are known, and the Pythagorean theorem is applied to find the missing side. The process involves identifying the hypotenuse and the other sides (labeled as 'a' and 'b'), setting up the equation, and solving for the missing variable 'x'. The video promises to cover a range of examples, from easy to more complex.

05:01

🔍 Using Trigonometry for Right Triangles

The second paragraph delves into using trigonometric ratios to solve for missing sides in right triangles when given one side and an angle. The SOHCAHTOA mnemonic is introduced to help remember the sine, cosine, and tangent ratios. The paragraph provides two examples: one where the sine ratio is used to find the opposite side when the hypotenuse is known, and another where the tangent ratio is used to find the adjacent side when the opposite side and the angle are known. The process includes setting up the trigonometric equation, solving for the unknown, and rationalizing the denominator if necessary.

10:03

📐 Law of Sines for Non-Right Triangles

In this paragraph, the focus shifts to non-right triangles where two angles and a side are given, and the goal is to find the missing side. The Law of Sines is introduced, with a formula that relates the ratios of sides to their opposite angles. The example given involves identifying the known angles and sides, setting up the equation according to the Law of Sines, and solving for the unknown side 'x'. The process highlights cross-multiplying and using a calculator to find the sine values of the given angles.

15:05

📉 Law of Cosines for Included Angles

The fourth paragraph discusses the use of the Law of Cosines to find a missing side in a non-right triangle when two sides and the included angle are known. The formula for the Law of Cosines is presented, and an example is worked through step by step. The process includes rearranging the formula to solve for the unknown side 'x', performing algebraic manipulations, and taking the square root to find the final value. The paragraph also explains how the Law of Cosines relates to the Pythagorean theorem in the case of a right triangle.

20:05

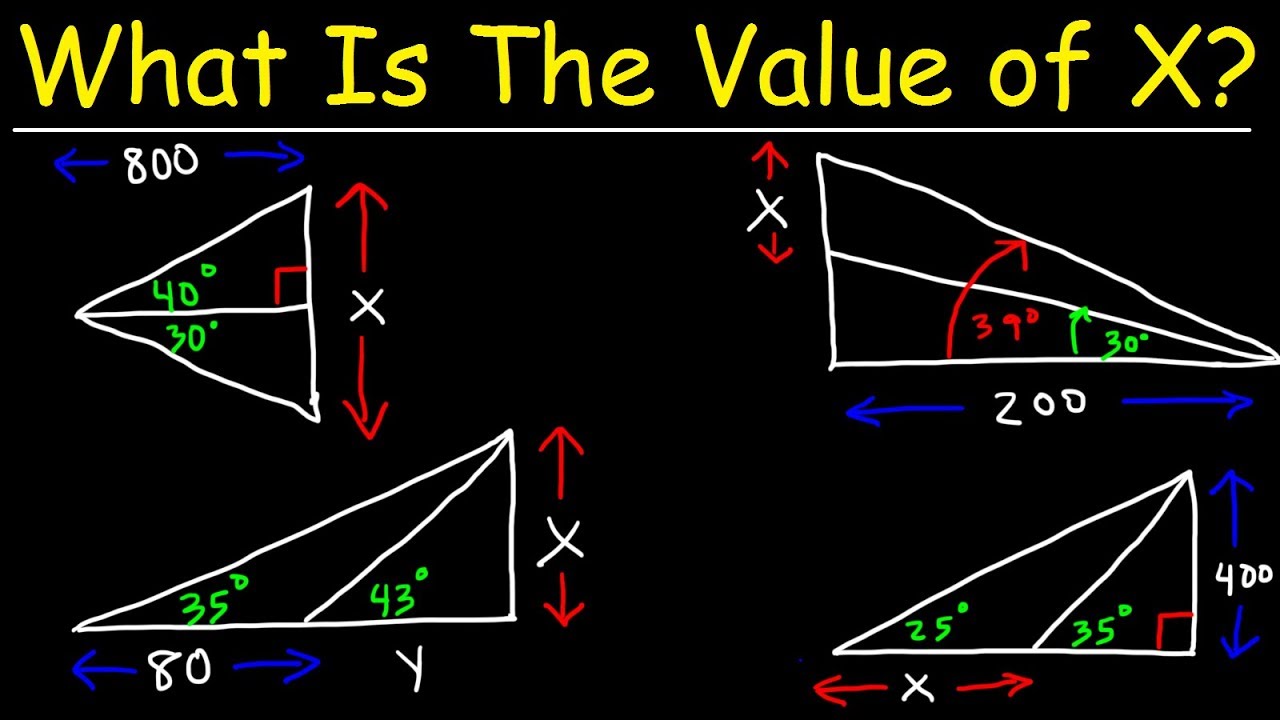
🌐 Solving Composite Triangles Using Tangent Ratio

This paragraph presents a more complex scenario involving a composite triangle where two missing side lengths need to be determined. The tangent ratio is used for the first triangle, and an equation is set up based on the given angle and sides. The second part of the triangle is solved using the tangent ratio again, but this time involving an angle of 20 degrees. The paragraph explains the process of setting up equations for each part of the triangle, solving for one variable in terms of another, and then combining the equations to find the missing sides.

25:06

📈 Geometric Mean and Pythagorean Theorem

The sixth paragraph explores the concept of the geometric mean in the context of right triangles formed by an altitude to the hypotenuse. It explains how to find the length of the altitude (x) as the geometric mean between two other sides. The paragraph then presents a problem involving a triangle with sides 8, 18, and x, and demonstrates how to find x, y, and z using the geometric mean and the Pythagorean theorem. The process involves recognizing the geometric mean, calculating the hypotenuse of smaller right triangles, and simplifying radicals to find the final lengths.

🔢 Solving Triangles with Algebraic Manipulation

The final paragraph concludes the video by showing an alternative method to solve the same triangle problem without relying on the geometric mean. It involves setting up three separate Pythagorean theorem equations for the three right triangles within the larger triangle. The paragraph demonstrates algebraic manipulation to combine and subtract these equations, ultimately solving for the three unknown variables x, y, and z. This method highlights the power of algebra in conjunction with the Pythagorean theorem to find missing side lengths in triangles.

Mindmap

Keywords

💡Pythagorean Theorem

The Pythagorean Theorem is a fundamental principle in geometry that states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This theorem is central to the video's theme as it is used to calculate missing side lengths in right-angled triangles. For example, the script mentions using the theorem with a triangle where 'a' is 6, 'b' (the missing side) is represented by 'x', and 'c' (the hypotenuse) is 10.

💡Hypotenuse

The hypotenuse is the longest side of a right-angled triangle, which is opposite the right angle. It is a key concept in the video as it is the side that is often calculated when applying the Pythagorean Theorem. The script uses the term when explaining that 'c' is the hypotenuse in the given examples, such as when 'c' equals 10 in the first example.

💡Square Root

A square root is a value that, when multiplied by itself, gives a specified number. In the context of the video, square roots are used to solve for the variable 'x' after setting up an equation using the Pythagorean Theorem. The script illustrates this when it says 'the square root of x squared is x' and when calculating the square root of 64 to find the value of 'x'.

💡Trigonometric Ratios

Trigonometric ratios, such as sine, cosine, and tangent, relate the angles of a triangle to the ratios of its sides. The video discusses the use of these ratios, particularly SOHCAHTOA, to find missing side lengths when given an angle and a side of a right triangle. For instance, the script explains using the sine ratio to find the missing side opposite to an angle of 30 degrees with a hypotenuse of 50 units.

💡SOHCAHTOA

SOHCAHTOA is a mnemonic used to remember the trigonometric ratios for sine, cosine, and tangent in relation to the angles and sides of a right triangle. The video uses this mnemonic to explain how to find a missing side when one side and an angle are known. Specifically, the script uses SOHCAHTOA to determine which trigonometric ratio to apply in various examples, like using the sine ratio for an angle of 30 degrees.

💡Law of Sines

The Law of Sines is a formula used in non-right triangles to relate the ratios of the lengths of a triangle's sides to the sines of its angles. The video introduces the Law of Sines to calculate a missing side length when two angles and one side of a triangle are known. The script demonstrates its use with an example where angles A and B are known, and side a is sought.

💡Law of Cosines

The Law of Cosines is a formula used in non-right triangles to calculate a missing side when two sides and the included angle are known. The video explains the application of the Law of Cosines with an example where the sides 'a' and 'b' and angle 'C' are given, and the missing side 'c' is calculated. The script shows the formula rearranged to solve for 'x' when 'a', 'b', and angle 'C' are known.

💡Geometric Mean

The geometric mean is a value that divides a line segment into two parts that have a specific ratio. In the context of the video, the geometric mean is used to find the length of an altitude from the hypotenuse of a triangle to the midpoint when two sides of the triangle are known. The script illustrates this with an example where 'x' is the geometric mean of 8 and 32, which is calculated as the square root of their product, resulting in 16.

💡Composite Triangle

A composite triangle is formed when a triangle is divided into two smaller right triangles by a line segment. The video addresses how to calculate missing side lengths in a composite triangle by setting up equations based on the tangent ratio and the Pythagorean Theorem. The script provides an example where two equations are formed for the two smaller right triangles, which are then solved to find the missing sides 'x' and 'y'.

💡Algebraic Manipulation

Algebraic manipulation involves the use of algebraic techniques to rearrange and combine equations to solve for unknown variables. The video demonstrates this process by subtracting one equation from another and then combining the result with a third equation to solve for the missing side lengths in a triangle. The script shows how to manipulate the equations derived from the Pythagorean Theorem for three right triangles to find the values of 'x', 'y', and 'z'.

💡Simplifying Radicals

Simplifying radicals is the process of expressing radicals in their simplest form by factoring out perfect squares. The video touches on this concept when calculating the square root of a number that is not a perfect square. The script mentions that 175 can be simplified by finding the largest perfect square that divides into it, which is 25 in the example, leading to the simplified radical form of '5 square root of 7'.

Highlights

Introduction to calculating missing side lengths of triangles using various methods.

Explanation of the Pythagorean theorem for right triangles.

Example of using the Pythagorean theorem with given sides a, b, and hypotenuse c.

Demonstration of solving for a missing side using algebraic manipulation.

Approach to finding a missing side when the hypotenuse and one leg are known.

Use of trigonometric ratios (SOHCAHTOA) for non-right triangles.

How to apply sine, cosine, and tangent ratios to find missing sides.

Example of using sine ratio to find a missing side opposite to a given angle.

Method for finding the hypotenuse when given an angle and an adjacent side.

Introduction of the Law of Sines for non-right triangles with two angles and a side known.

Formula and application of the Law of Sines to find a missing side.

Use of the Law of Cosines for triangles with two sides and the included angle known.

Explanation of how the Law of Cosines relates to the Pythagorean theorem in right triangles.

Solving a composite triangle problem using tangent ratios and algebraic substitution.

Finding missing sides in a geometric sequence using the concept of geometric mean.

Approach to solving a triangle problem with three variables using three Pythagorean theorem equations.

Final summary of methods for calculating missing side lengths of triangles.

Transcripts

Browse More Related Video

How To Calculate The Missing Angle In a Triangle

How To Solve Two Triangle Trigonometry Problems

How to Use the Law of Sines in Trigonometry (Precalculus - Trigonometry 32)

Pythagorean Theorem - Basic Introduction

Trigonometry - How To Solve Right Triangles

5.6.1 Law of Cosines: Solving Triangles (SAS, SSS)

Related Tags

Triangle Calculation Pythagorean Theorem Trigonometry SohCahToa Geometric Mean Right Triangles Algebraic Methods Mathematics Tutorial Educational Content Geometry Problems