Math Antics - The Pythagorean Theorem
TLDRIn this Math Antics lesson, Rob introduces the Pythagorean Theorem, explaining its origins and significance. He clarifies that a theorem is a proven mathematical statement and attributes the theorem to Pythagoras. The video covers essential background knowledge on angles, triangles, exponents, and square roots, necessary for understanding the theorem. The Pythagorean Theorem relates the sides of a right triangle, stating that a² + b² = c². Through examples and practical applications, Rob demonstrates how to use the theorem to find unknown side lengths and verify if a triangle is a right triangle. The lesson emphasizes practicing real math problems to master the theorem.
Takeaways
- 📚 The Pythagorean Theorem is a proven mathematical statement that describes the relationship between the sides of a right triangle.
- 🧐 The theorem is named after Pythagoras, an ancient Greek philosopher, though it's not certain he proved it himself.
- 📐 The theorem applies exclusively to right triangles, which have one right angle marked with a square symbol.
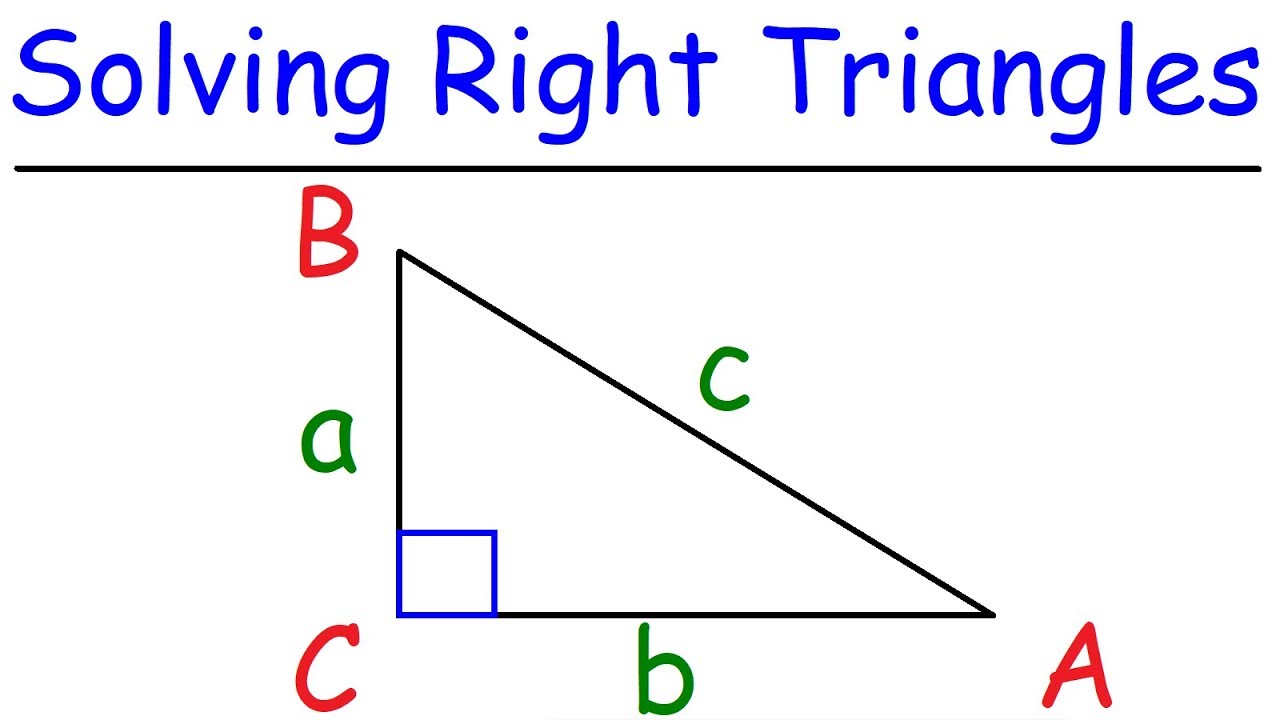
- 🔍 To use the theorem, one must identify the hypotenuse (the longest side opposite the right angle) and the legs (the other two sides).
- 📈 The theorem is expressed as a^2 + b^2 = c^2, where 'a' and 'b' are the legs and 'c' is the hypotenuse.
- 📝 Understanding the theorem requires knowledge of angles, triangles, exponents, square roots, and basic algebra.
- 🌟 A special example is the '3, 4, 5 triangle', which demonstrates the theorem's principle regardless of the units of measurement.
- 🔑 The theorem is useful for finding the length of an unknown side of a right triangle when two sides are known.
- 📏 It can also be used to verify if a triangle is a right triangle by testing if the side lengths satisfy the theorem.
- 📉 If the theorem does not hold for a given set of three side lengths, the triangle is not a right triangle.
- 📚 Mastery of the Pythagorean Theorem involves practice and a solid foundation in related mathematical skills.
Q & A
What is a theorem in mathematics?
-A theorem in mathematics is a statement that has been proven to be true from other things that are either known or accepted to be true.
Who is Pythagoras and what is his connection to the Pythagorean Theorem?
-Pythagoras was a philosopher and mathematician from ancient Greece. He is credited with proving the Pythagorean Theorem, although historians are not completely sure if it was actually him or one of his students or followers.
What is the Pythagorean Theorem and what does it describe?
-The Pythagorean Theorem describes an important geometric relationship between the three sides of a right triangle. It states that for a right triangle with legs 'a' and 'b' and hypotenuse 'c', the equation 'a squared' plus 'b squared' equals 'c squared' holds true.
What mathematical concepts are prerequisites for understanding the Pythagorean Theorem?
-To understand the Pythagorean Theorem, you need to know about angles and triangles, exponents, square roots, and basic algebra, including variables and solving algebraic equations involving exponents.
Why is it important to identify the hypotenuse in a right triangle when using the Pythagorean Theorem?
-Identifying the hypotenuse is important because it is the longest side of the right triangle and is opposite the right angle. In the theorem, 'c' represents the length of the hypotenuse, and knowing this allows you to apply the theorem correctly.
What is a '3, 4, 5 triangle' and how does it relate to the Pythagorean Theorem?
-A '3, 4, 5 triangle' is a special example of a right triangle where the sides have relative lengths of 3, 4, and 5. It helps illustrate the Pythagorean Theorem because when you square the lengths of the two shorter sides (3 and 4) and add them together, they equal the square of the longest side (5), demonstrating the theorem's validity.
How can the Pythagorean Theorem be used to find the length of an unknown side of a right triangle?
-The Pythagorean Theorem can be used by substituting the known side lengths into the equation 'a squared' plus 'b squared' equals 'c squared' and then solving for the unknown side. This process involves algebraic manipulation to isolate the unknown variable and then applying the square root to find its value.
Can the Pythagorean Theorem be used to determine if a triangle is a right triangle?
-Yes, the Pythagorean Theorem can be used to test if a triangle is a right triangle by checking if the relationship 'a squared' plus 'b squared' equals 'c squared' holds true for the given side lengths. If the equation does not hold, the triangle is not a right triangle.
What is the significance of the Pythagorean Theorem in practical applications?
-The Pythagorean Theorem is a useful tool in various practical applications, such as construction, engineering, and even in everyday situations where one needs to determine distances or lengths involving right triangles.
How does the Pythagorean Theorem relate to a unit square cut in half along its diagonal?
-When a unit square is cut in half along its diagonal, it forms two right triangles, each with legs of length 1 unit. Using the Pythagorean Theorem, you can determine the length of the diagonal (the hypotenuse), which is the square root of 2 units.
Outlines
📚 Introduction to the Pythagorean Theorem
In the first paragraph, Rob introduces the Pythagorean Theorem, a fundamental principle in geometry that relates the three sides of a right triangle. He explains that a theorem is a proven statement in mathematics and provides some historical context about Pythagoras, the ancient Greek philosopher credited with the theorem, although it's noted that it might have been his students who actually proved it. Rob emphasizes the importance of understanding angles, triangles, exponents, and square roots, as well as basic algebra, to effectively use the theorem. He then presents the theorem's formula: a² + b² = c², specifically for right triangles, and explains the significance of identifying the hypotenuse and the legs of the triangle.
🔍 Demonstrating the Pythagorean Theorem with a 3-4-5 Triangle
The second paragraph delves into a practical demonstration of the Pythagorean Theorem using a '3-4-5' right triangle, where the sides are in the ratio of 3, 4, and 5. Rob illustrates the process of squaring each side and shows that the sum of the squares of the two legs equals the square of the hypotenuse, both arithmetically (9 + 16 = 25) and geometrically, through the arrangement of unit squares. This visual and mathematical proof reinforces the theorem's validity and provides a clear example of its application. The paragraph also discusses the theorem's utility in solving for unknown sides of right triangles when two sides are known.
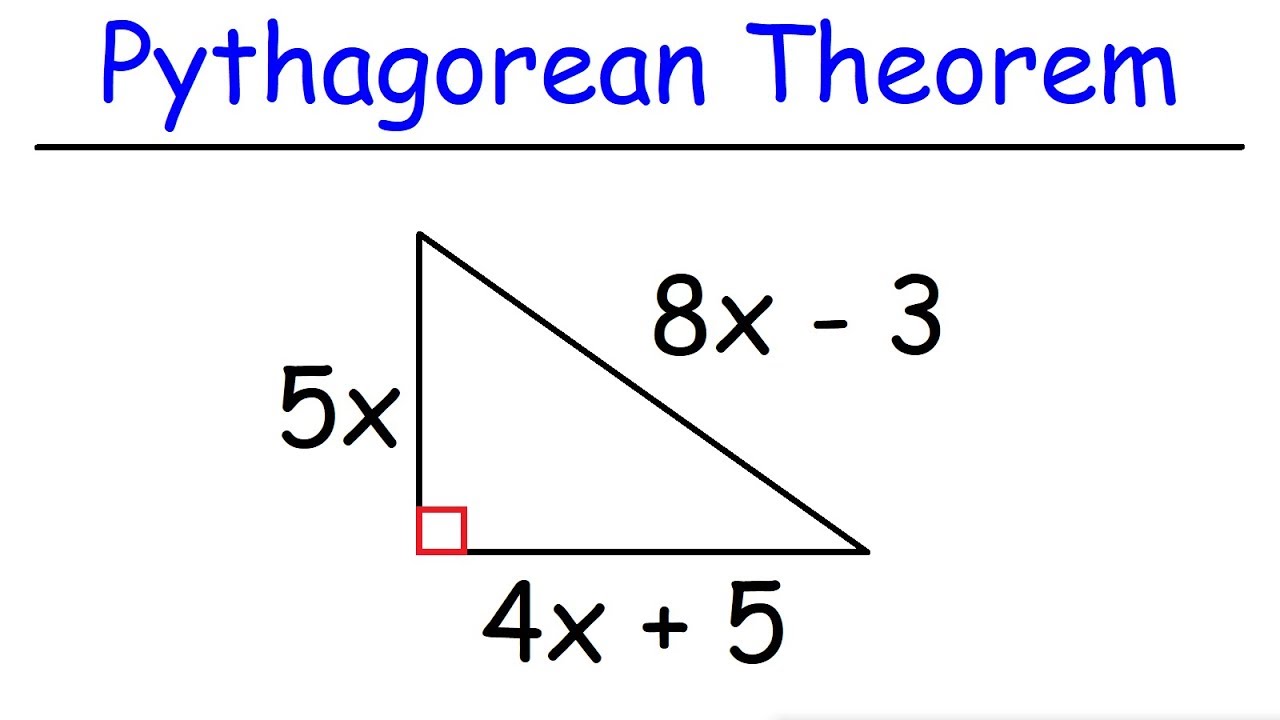
🛠 Applying the Pythagorean Theorem to Solve for Unknown Sides
In the third paragraph, the script focuses on applying the Pythagorean Theorem to solve for unknown sides in right triangles. It provides step-by-step algebraic methods to find the hypotenuse when the legs are known, and vice versa. Rob also explains how to handle the square root operation when solving for an unknown side, noting that while a calculator can provide a decimal approximation, it's often acceptable to leave the answer in the form of a square root, especially if it's an irrational number. The paragraph includes examples with different combinations of known and unknown sides, showcasing the theorem's versatility in problem-solving.
📏 Using the Pythagorean Theorem to Verify Right Triangles
The final paragraph discusses an additional application of the Pythagorean Theorem: verifying whether a triangle is a right triangle by testing if its side lengths satisfy the theorem's equation. Rob uses an example where the sides are 3 cm, 4 cm, and an unknown hypotenuse. After calculating, he shows that the sides do not satisfy the theorem, concluding that the triangle in question is not a right triangle. The paragraph wraps up with a reminder of the importance of practicing math problems to gain proficiency and an invitation to learn more on the Math Antics website.
Mindmap
Keywords
💡The Pythagorean Theorem
💡Right Triangle
💡Hypotenuse
💡Legs of a Triangle
💡Square
💡Exponents
💡Square Roots
💡Algebra
💡Variables
💡3, 4, 5 Triangle
Highlights
The Pythagorean Theorem is a proven statement in math that describes a geometric relationship in right triangles.
Pythagoras, an ancient Greek philosopher, is credited with the theorem, though it may have been proven by his students or followers.
Understanding the Pythagorean Theorem requires knowledge of angles, triangles, exponents, and square roots.
Basic algebra skills, including variables and solving equations with exponents, are necessary to apply the theorem.
The theorem states that in a right triangle with legs 'a' and 'b', and hypotenuse 'c', a squared plus b squared equals c squared.
The theorem only applies to right triangles, identified by one right angle marked with a square symbol.
The hypotenuse is the longest side opposite the right angle, and the legs are the other two sides forming the right angle.
The Pythagorean Theorem helps find the length of an unknown side in a right triangle when two sides are known.
A special example is the '3, 4, 5 triangle', illustrating the theorem with sides in proportion to these numbers.
The theorem is used to solve for the hypotenuse when two legs' lengths are known, by setting up and solving an equation.
If the hypotenuse and one leg are known, the theorem can be used to find the length of the other leg.
The theorem can determine the distance across the diagonal of a unit square by treating it as two right triangles.
The Pythagorean Theorem can also verify if a triangle is a right triangle by testing the relationship of its sides.
An example demonstrates how the theorem can disprove a triangle as a right triangle if the sides do not satisfy the theorem.
The theorem's effectiveness depends on a range of math skills, including practice in solving real math problems.
The video concludes by emphasizing the importance of practice and the resources available at www.mathantics.com.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: