Probability Distribution Functions (PMF, PDF, CDF)

zedstatistics
1 Mar 202016:16
EducationalLearning
32 Likes 10 Comments

TLDRThis video from Zed Statistics dives into the concept of probability distribution functions, focusing on both discrete and continuous variables. It explains the difference between Probability Mass Function (PMF) for discrete variables and Probability Density Function (PDF) for continuous ones. The video uses intuitive examples, such as rolling a dice and the height distribution of women, to illustrate these concepts. It also covers Cumulative Distribution Function (CDF), showing how to derive it from PMF or PDF and vice versa. The script aims to make these statistical concepts accessible without overwhelming the audience with complex formulas, making it an informative resource for beginners.

Takeaways
  • 📚 The video introduces the concept of probability distribution functions, focusing on discrete and continuous variables.
  • 🎲 Discrete variables use a Probability Mass Function (PMF), which calculates the probability of each discrete outcome, such as rolling a die.
  • 📊 Continuous variables utilize a Probability Density Function (PDF), which represents the likelihood of outcomes in a continuous range, like human height.
  • 🔢 The acronym PMF stands for Probability Mass Function and is associated with discrete variables, whereas PDF stands for Probability Density Function and is used for continuous variables.
  • 👁️ Be cautious with the term 'PDF' as it can refer to both Probability Distribution Functions in a broad sense and Probability Density Functions specifically for continuous variables.
  • 📈 Cumulative Distribution Function (CDF) is a function used for both discrete and continuous variables to represent the cumulative probability up to a certain point.
  • 🚀 The video uses the example of a die roll to illustrate PMF and how to construct a CDF by summing probabilities of outcomes.
  • 📊 For continuous distributions, the video explains how to derive the CDF from the PDF by looking at the gradient of the PDF curve, which represents the density of outcomes around a certain point.
  • 🔍 The gradient of the CDF at a point is equal to the PDF at that point, indicating the density or concentration of outcomes in that area.
  • ⚖️ The video clarifies that the area under the PDF curve to the left of a certain point on the x-axis gives the value of the CDF at that point.
  • 🧮 For those familiar with calculus, the relationship between PDF and CDF can be described using differentiation and integration, with the PDF being the derivative of the CDF and the CDF being the integral of the PDF from negative infinity to a given x.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is probability distribution functions, focusing on the concepts of discrete and continuous variables, probability mass functions (PMF), and probability density functions (PDF).

  • What is a probability mass function (PMF)?

    -A probability mass function (PMF) is a function that describes the probability of each discrete outcome. It is used for discrete variables where outcomes are countable and distinct, like the outcomes of rolling a dice.

  • What is a probability density function (PDF)?

    -A probability density function (PDF) is used for continuous variables. Unlike PMF, PDF provides the probability of a range of outcomes rather than specific outcomes. It is used to describe the likelihood of results within a continuous distribution, such as the height of women.

  • What does the acronym CDF stand for?

    -CDF stands for cumulative distribution function. It is a function that describes the cumulative probability that a random variable X takes a value less than or equal to a certain value.

  • How is the cumulative distribution function (CDF) related to the probability mass function (PMF)?

    -The cumulative distribution function (CDF) is related to the probability mass function (PMF) in that the CDF is the cumulative sum of the PMF. It shows the probability of a discrete variable taking on a value less than or equal to a certain point.

  • What is the significance of the term 'cumulative' in the context of probability?

    -The term 'cumulative' in probability refers to the sum of probabilities up to a certain point. In the context of a cumulative distribution function, it represents the total probability of all outcomes that are less than or equal to a specified value.

  • How does the video illustrate the concept of a rigged dice?

    -The video illustrates a rigged dice by changing the probabilities of rolling certain numbers. Instead of having an equal chance of rolling any number between 1 and 6, the rigged dice has a 25% chance of rolling 1, 2, 5, or 6, and no chance of rolling 3 or 4.

  • What is the difference between a discrete and a continuous variable in terms of probability?

    -A discrete variable has a countable number of possible outcomes, such as the result of rolling a dice. A continuous variable, on the other hand, can take on any value within a range, such as the height of a person, which can have infinite decimal points.

  • How does the video explain the relationship between the PDF and the CDF?

    -The video explains that the PDF can be derived from the CDF by calculating the gradient (slope) of the CDF at a given point. Conversely, the CDF can be obtained by integrating the PDF from negative infinity to a specific value.

  • What is the shape of the cumulative distribution function (CDF) for a normal probability density function (PDF)?

    -The shape of the CDF for a normal PDF is an S-curve, which is a typical representation of a cumulative probability distribution that starts at 0, increases to a peak, and then asymptotically approaches 1.

  • How can one estimate the probability density from the cumulative distribution function (CDF)?

    -One can estimate the probability density from the CDF by finding the gradient of the CDF at a specific point. The steeper the gradient, the higher the probability density at that point.

  • What is the final value of a cumulative distribution function (CDF)?

    -The final value of a cumulative distribution function (CDF) is 1, representing the total probability that a random variable is less than or equal to the maximum value of the distribution.

Outlines
00:00
🎲 Introduction to Probability Distribution Functions

The video script begins with an introduction to probability distribution functions, focusing on the distinction between discrete and continuous variables. Discrete variables are associated with a probability mass function (PMF), which calculates the probability of each specific outcome, while continuous variables use a probability density function (PDF) to express the likelihood of outcomes across a range. The narrator clarifies potential confusion around the acronym 'PDF,' emphasizing its use for continuous variables. Cumulative distribution functions (CDFs) are also introduced as a tool for calculating the probability of outcomes up to a certain point, with an example of rolling a standard six-sided die to illustrate the concepts.

05:00
📊 Discrete Variables and Cumulative Probability

In this section, the script delves deeper into discrete variables, using the example of a rigged die that does not allow for the outcomes of three or four. The probability mass function (PMF) is adjusted accordingly, with each of the remaining outcomes having an equal chance of 25%. The cumulative distribution function (CDF) is then explored, showing how it represents the probability of rolling a number less than or equal to a certain value. The script explains that the CDF will have a flat gradient where outcomes are impossible, such as between three and four on the rigged die, indicating no probability mass in those regions.

10:01
📚 Continuous Variables and Probability Density

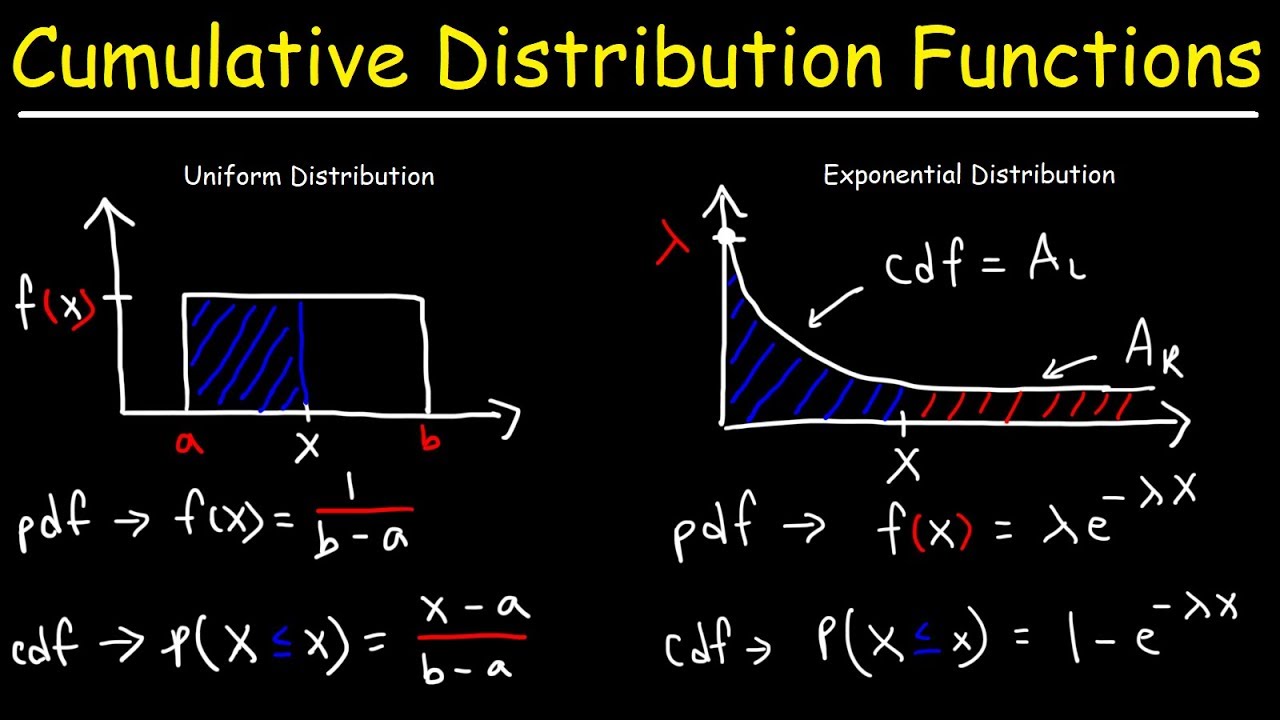
The script shifts focus to continuous variables, exemplified by the distribution of women's heights with a mean of 165 centimeters and a standard deviation that creates a normal distribution curve. The probability density function (PDF) is described as a way to visualize the likelihood of different heights, with the peak of the curve indicating the most probable height. The cumulative distribution function (CDF) for continuous variables is introduced as an 'S-curve,' showing the proportion of the distribution up to a certain height. The relationship between the PDF and CDF is explored, demonstrating how the CDF can be derived from the area under the PDF curve.

15:02
🔍 Calculating Gradient and Area for PDF and CDF

The final paragraph explains how to derive the probability density function (PDF) from the cumulative distribution function (CDF) by calculating the gradient at a given point. The script uses the height example again, showing that the gradient of the CDF at 165 centimeters corresponds to the peak of the PDF, indicating the most probable height. It also explains that the area under the PDF to the left of a point represents the value on the CDF. The relationship between differentiation and integration in calculus is briefly mentioned, with the PDF represented as the derivative of the CDF and the CDF as the integral of the PDF from negative infinity to a given value. The video concludes with a prompt for viewers to check out more educational content on the provided website and to continue sending feedback and suggestions.

Mindmap
Keywords
💡Probability Distribution
Probability distribution refers to the likelihood of each possible outcome of a random variable. In the video, it is the central theme, explaining how the probability of outcomes can be represented either for discrete or continuous variables. The script uses examples such as rolling a dice for discrete outcomes and the height of women for continuous outcomes to illustrate these distributions.
💡Discrete Variables
Discrete variables are those that can take on a countable number of distinct values. In the script, rolling a dice is used as an example of a discrete variable, where each face of the dice represents a possible outcome with a specific probability, such as 1/6 for a fair dice.
💡Continuous Variables
Continuous variables, as opposed to discrete, can take on any value within a given range. The video uses the example of the height of women, which can vary infinitely between certain points, to demonstrate continuous variables and their associated probability distributions.
💡Probability Mass Function (PMF)
The Probability Mass Function (PMF) is a function that describes the probability of a discrete random variable being exactly equal to some value. The script explains PMF as the function that assigns the probability of each outcome for a discrete variable, like the probability of rolling a specific number on a dice.
💡Probability Density Function (PDF)
A Probability Density Function (PDF) defines the likelihood of a continuous variable's value falling within a particular range. The video clarifies that PDF is used for continuous variables, like the height of women, and it represents the density of the probability rather than the probability itself.
💡Cumulative Distribution Function (CDF)
The Cumulative Distribution Function (CDF) is a function that describes the cumulative probability up to a certain point for either discrete or continuous variables. In the script, CDF is introduced as a way to sum up the probabilities of all outcomes less than or equal to a specific value, like the probability of rolling a number less than or equal to four on a dice.
💡S-Curve
An S-Curve is a graphical representation of a cumulative distribution function, especially for a normal distribution, which resembles the letter 'S'. The video describes the typical shape of the CDF for a normal distribution, such as the height of women, as an S-Curve, indicating the accumulation of probability from 0 to 1.
💡Mean
The mean, often referred to as the average, is a measure of central tendency in statistics. In the context of the video, the mean is used to describe the average height of women in the continuous distribution example, where 165 centimeters is given as the mean height.
💡Standard Deviation
Standard deviation is a measure that quantifies the amount of variation or dispersion in a set of values. The script mentions standard deviation in the context of the height of women, indicating the spread of heights around the mean, with fewer women being very short or very tall.
💡Gradient
In the video, the term 'gradient' is used to describe the slope or steepness of the cumulative distribution function (CDF) at a particular point. The gradient is related to the probability density function (PDF), with a higher gradient indicating a higher density of the distribution around that point, such as the peak at the mean height in the women's height example.
Highlights

Introduction to the concept of probability distribution functions with a focus on discrete and continuous variables.

Explanation of discrete variables and the use of Probability Mass Function (PMF).

Clarification of the acronym PMF and its association with discrete outcomes.

Introduction of Probability Density Function (PDF) for continuous variables.

Differentiation between PMF and PDF in terms of discrete and continuous outcomes.

Discussion on the Cumulative Distribution Function (CDF) for both discrete and continuous variables.

Example of a discrete variable using a six-sided dice and its PMF.

Illustration of how to construct a cumulative probability for a dice roll.

Explanation of the properties of a cumulative distribution function, with the final value reaching 1.

Demonstration of a rigged dice example to show changes in cumulative probability.

Transition to continuous distributions with the example of female height distribution.

Description of the normal PDF shape for the height of women with a mean and standard deviation.

Linking the PDF with the CDF and explaining the S-curve of the CDF.

Deriving cumulative probability from the PDF using the example of female height.

Exploring the relationship between the gradient of the CDF and the PDF.

Calculating the gradient at a specific point on the CDF to find the corresponding PDF value.

Summary of the relationship between CDF and PDF through differentiation and integration.

Conclusion of the video with a call to action for viewers to check out more resources and subscribe.

Transcripts

Browse More Related Video

Cumulative Distribution Functions and Probability Density Functions

5. Discrete Random Variables I

6.1.1 The Standard Normal Distribution - Discrete and Continuous Probability Distributions

Elementary Stats Lesson #12

Lecture 14: Location, Scale, and LOTUS | Statistics 110

Mathematical Statistics, Lecture 1

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
ProbabilityStatisticsDiscrete VariablesContinuous VariablesPMFPDFCDFDice RollNormal DistributionEducationalVisual Explanation