Lecture 14: Location, Scale, and LOTUS | Statistics 110

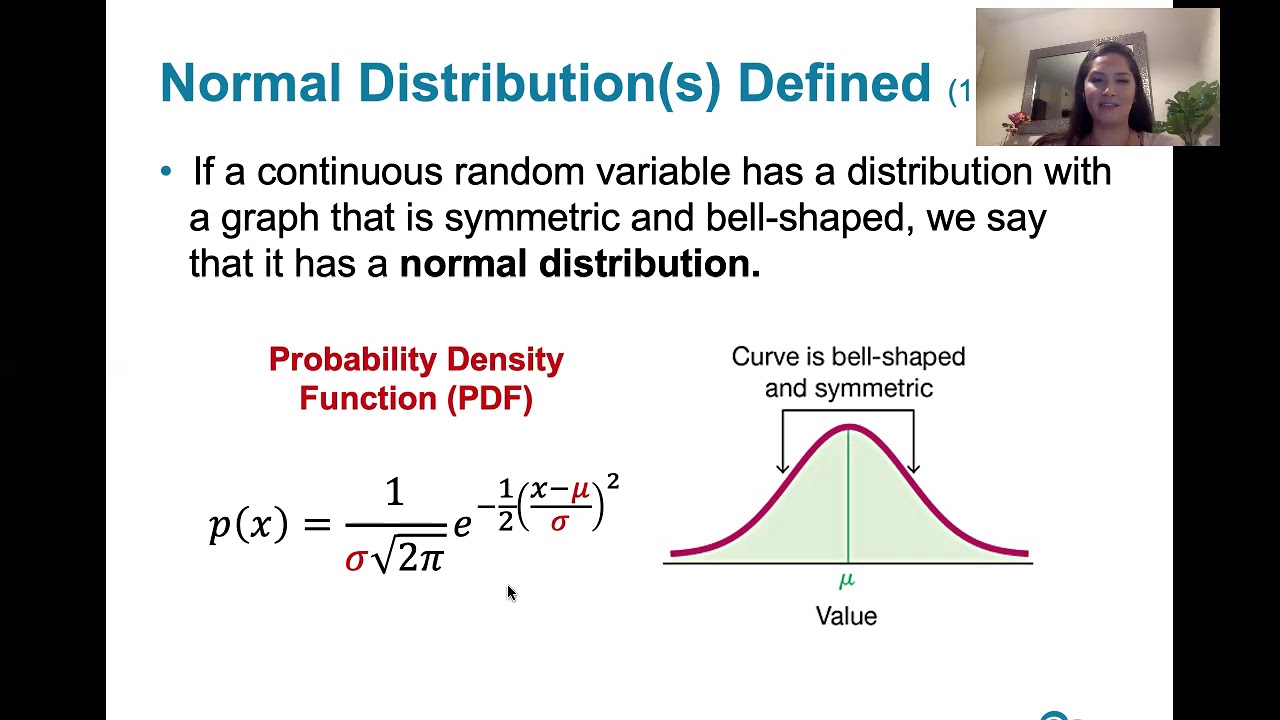
The paragraph begins with a review of the standard normal distribution, denoted as Z, which has a mean of 0 and a variance of 1. The cumulative distribution function (CDF) of the standard normal is symbolized by the capital Phi and cannot be expressed in closed form. The properties of the standard normal are discussed, including its mean and variance, and the fact that all odd moments (E[Z^n] for odd n) are zero due to symmetry. The concept of moments is introduced, and the importance of symmetry in understanding the distribution is highlighted. The general normal distribution is then introduced as X = μ + σZ, where μ is the mean (or location) and σ is the standard deviation (or scale).

This section delves into the properties of variance, emphasizing that variance is not linear and cannot be negative. It explains how adding a constant to a random variable does not affect its variance, but multiplying by a constant c results in the variance being multiplied by c^2. The importance of squaring the constant when applying it to the variance is stressed to avoid computational errors. The paragraph also clarifies that the variance of a sum of two random variables is not simply the sum of their variances unless the variables are independent. The concept of standardization for normal distributions is introduced as X = μ + σZ, and the reverse process is also explained.

The paragraph focuses on deriving the probability density function (PDF) of a general normal distribution with mean μ and variance σ^2. It uses the standardization technique to transform the random variable X into a standard normal Z, and then applies the chain rule from calculus to find the derivative of the CDF, which yields the PDF. The process is demonstrated to be straightforward once the PDF of the standard normal distribution is known. The concept of the 68-95-99.7% rule is introduced as a rule of thumb for the normal distribution, indicating the probability of a normal random variable falling within a certain number of standard deviations from the mean.

The discussion shifts to the Poisson distribution, which is characterized by having a mean and variance both equal to lambda (λ). The process of finding the variance involves using the moment-generating function (MGF) of the Poisson distribution and applying derivatives to find E[X^2]. The sum of λ^k/k! is derived using the Taylor series expansion of e^λ, and the variance is ultimately found by subtracting the square of the mean from E[X^2]. The properties of the Poisson distribution are highlighted, including the fact that the mean equals the variance.

The paragraph tackles the calculation of the variance for a binomial distribution. It outlines three potential methods for finding the variance: a direct but tedious calculation using the binomial PMF, an easy method that relies on the variance of independent sums (which is not yet proven), and a compromise method using indicator random variables. The compromise method involves squaring the binomial expression, summing over all terms, and then applying expected values to simplify the expression. The result is the variance of the binomial distribution, which is given by np(1-p), where n is the number of trials and p is the probability of success in each trial.

The final paragraph provides an explanation for the Law of the Unconscious Statistician (LOTUS), particularly for discrete random variables. LOTUS states that the expected value of a function of a random variable can be computed as a sum of the function times the probability mass function (PMF) without first determining the distribution of the function. The proof involves considering the sum over all possible values of the random variable and grouping them into 'super pebbles' based on their values. The double sum representation is used to show that the expected value can be computed by first summing over all values of the random variable and then summing over the corresponding probabilities, leading to the conclusion that LOTUS holds true.