Finding the equation of a periodic function from a graph or sketch

Joel Speranza Math
24 Mar 201508:54
EducationalLearning
32 Likes 10 Comments

TLDRThis video tutorial guides viewers on how to derive the equation of a periodic function, such as a cosine curve, from its graph. It begins by identifying key characteristics like amplitude, maximum, and minimum values to determine the equation's parameters. The process involves calculating the center (D value), amplitude (a value), phase shift (C value), and period to find the B value. The systematic approach includes mathematical formulas and examples, ultimately leading to the equation of the form y = a*cos(Bx + C) + D, which can be used to describe the graph.

Takeaways
  • ๐Ÿ“š The learning goal is to derive the equation of a periodic function from its graph.
  • ๐Ÿ” The video assumes the function is a cosine curve, but it could also be an S curve.
  • ๐Ÿ“‰ The general form of a periodic equation is y = a*cos(Bx + C) + D.
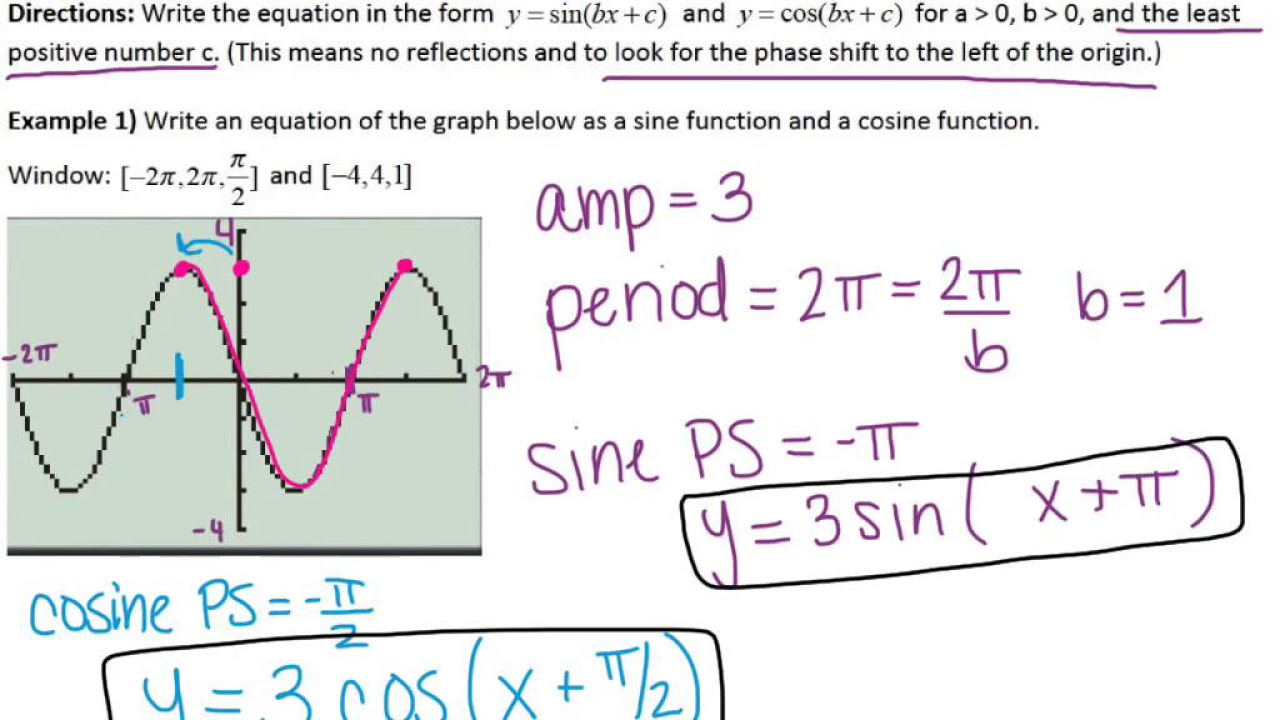
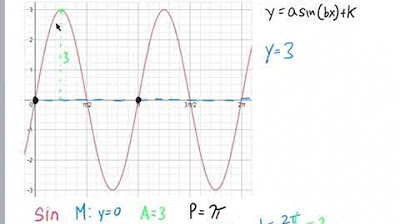
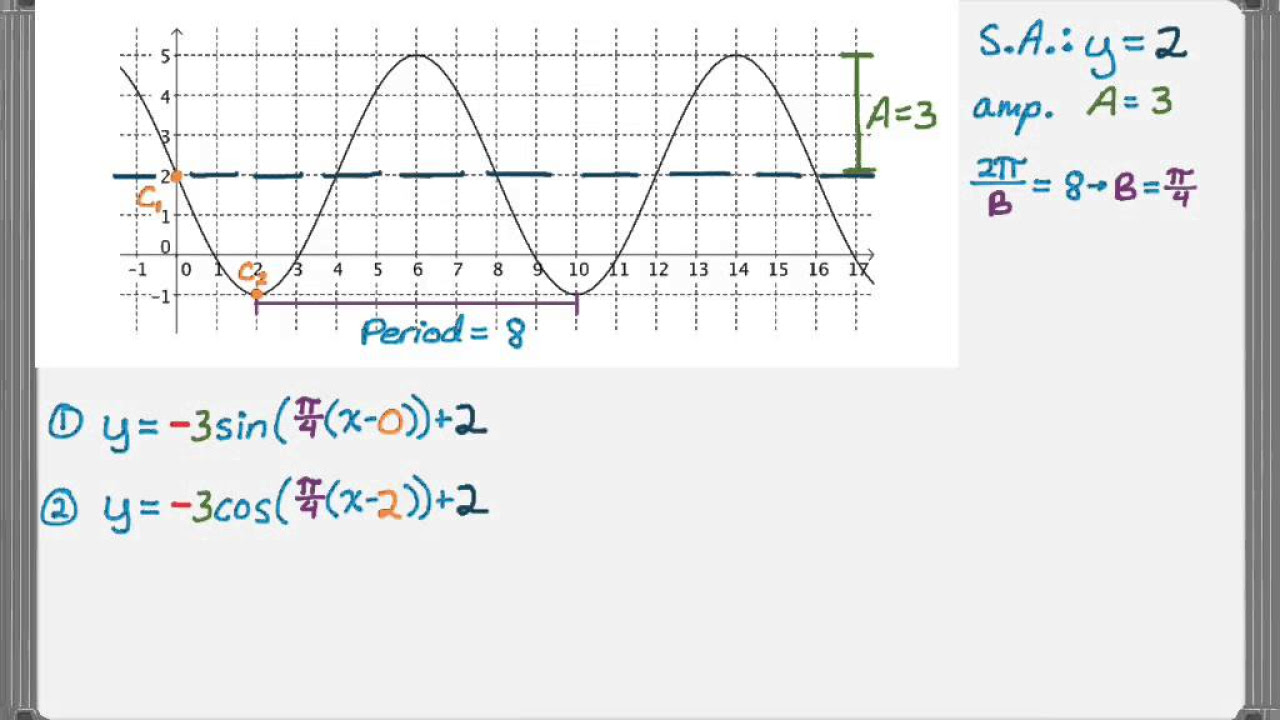
  • ๐Ÿ“ˆ The function's amplitude (a) is the distance from the center to the maximum or minimum, found to be 2.
  • ๐Ÿ“ The center (median) of the function is calculated by averaging the maximum and minimum, resulting in 4.
  • ๐Ÿ”ข The D value represents the vertical shift from the x-axis, which is determined to be 4.
  • ๐Ÿ”„ The C value indicates horizontal shift, found to be -1 by observing the starting position of the function.
  • ๐Ÿ” The choice between a cosine or S curve depends on the starting position and direction of the function's movement.
  • โฑ The B value is related to the period of the function, calculated using the formula: period = 2ฯ€/B.
  • ๐Ÿ“ The period of the graph is determined by measuring the time it takes for the function to repeat, found to be 12 units.
  • ๐Ÿงฎ The B value is calculated to be ฯ€/6 by solving the period formula with the given period.
  • ๐Ÿ”‘ The final equation derived from the graph is y = 2*cos(ฯ€/6 * x - 1) + 4.
Q & A

  • What is the learning goal of the video?

    -The learning goal of the video is to enable viewers to find the equation of a periodic function by the end of the video, specifically for a function that could be represented by a cosine curve.

  • What are the two possible types of periodic functions mentioned in the video?

    -The two possible types of periodic functions mentioned are an S curve and a cosine curve.

  • What is the general form of a periodic equation?

    -The general form of a periodic equation is y = a * cos(b * x + c) + d, where a, b, c, and d are constants that define the specific characteristics of the function.

  • How can you determine the maximum and minimum values of the periodic function from the graph?

    -You can determine the maximum and minimum values by looking at the highest and lowest points on the graph. In the video, the maximum is 6 and the minimum is 2.

  • What is the center or median of the periodic function, and how is it calculated?

    -The center or median of the periodic function is the midpoint between the maximum and minimum values. It is calculated by adding the maximum and minimum values together and then dividing by two. In the video, (6 + 2) / 2 = 4.

  • What does the 'D' value in the equation represent, and how is it determined?

    -The 'D' value in the equation represents the vertical shift of the function from the x-axis. It is determined by finding the center or median of the function. In the video, the 'D' value is 4.

  • How is the amplitude of the function determined, and what does it represent?

    -The amplitude is determined by measuring the distance from the center to the maximum or minimum value. It represents the peak deviation of the function from its center. In the video, the amplitude is 2.

  • What is the 'C' value in the equation, and how does it relate to the phase shift of the function?

    -The 'C' value in the equation represents the phase shift of the function. It is determined by how much the function has shifted from the origin. In the video, the 'C' value is -1, indicating a shift to the right by one unit.

  • Why might one choose a cosine curve over an S curve, and vice versa?

    -One might choose a cosine curve over an S curve if the function appears to start from the top and move down and back up to the top again, as cosine curves do. Conversely, an S curve might be chosen if the function starts from the middle, moves up to the top, comes back, and returns to the middle, which is characteristic of S curves.

  • How is the 'B' value in the equation determined, and what does it represent?

    -The 'B' value is determined using the formula for the period of the function, which is period = 2ฯ€/B. The 'B' value represents the horizontal compression or stretch of the cosine function, affecting its period. In the video, the 'B' value is calculated to be ฯ€/6.

  • What is the final equation of the periodic function derived from the video?

    -The final equation of the periodic function derived from the video is y = 2 * cos(ฯ€/6 * x - 1) + 4.

Outlines
00:00
๐Ÿ“š Introduction to Finding Periodic Function Equations

The video aims to teach viewers how to derive the equation of a periodic function, specifically a cosine curve, by observing its graph. The speaker begins by identifying the general form of a cosine function, y = a*cos(Bx + C) + D, and explains the significance of each variable. They demonstrate how to determine the amplitude (a), vertical shift (D), and phase shift (C) by analyzing the graph's maximum and minimum values, as well as its center. The amplitude is found to be 2, and the vertical shift (D) is determined to be 4, based on the graph's oscillation between a maximum of 6 and a minimum of 2. The center of the graph is calculated to be 4, which corresponds to the D value in the equation.

05:02
๐Ÿ” Determining Phase Shift and Amplitude of the Cosine Function

Continuing from the previous explanation, the speaker discusses how to find the phase shift (C) and amplitude (a) of the cosine function. They assume the starting position of the cosine curve and deduce that the phase shift is -1, as the function has moved one unit to the right from the origin. The amplitude, already identified as 2, is the distance from the center to the maximum or minimum of the graph. The speaker also briefly touches on the alternative scenario where the curve could be a sigmoid (S curve), which would have a different phase shift and starting position. The summary of the cosine function equation thus far is y = 2*cos(Bx - 1) + 4.

๐Ÿงฎ Calculating the Period and B Value of the Cosine Function

In the final part of the explanation, the speaker focuses on calculating the period and the B value of the cosine function. They use the formula for the period of a cosine function, which is Period = 2ฯ€/B, and demonstrate how to find the period by measuring the time it takes for the graph to repeat itself. The period is determined to be 12 units, based on the graph's repetition from 1 to 13 on the x-axis. Using this period, the B value is calculated by rearranging the period formula to solve for B, resulting in B = ฯ€/6. The complete equation of the cosine function is then presented as y = 2*cos(ฯ€/6 * x - 1) + 4. The speaker emphasizes the systematic approach taken to derive the equation from the graph, which involved finding the center, amplitude, phase shift, and finally the B value.

Mindmap
Keywords
๐Ÿ’กPeriodic function
A periodic function is a type of function that repeats its values at regular intervals or periods. In the context of the video, the periodic function refers to a mathematical function that oscillates between a maximum and minimum value, and the shape of its graph repeats over a certain interval. The script discusses finding the equation of such a function, which could be either a cosine curve or an S curve.
๐Ÿ’กCosine curve
A cosine curve is a specific type of periodic function that follows the pattern of the cosine trigonometric function. It is characterized by its smooth, wave-like shape that oscillates between -1 and 1. In the video, the cosine curve is assumed to be the shape of the graph, and the process of determining its equation is explained step by step.
๐Ÿ’กAmplitude
Amplitude in a periodic function refers to the distance from the center line (or median) to the peak (maximum) or trough (minimum) of the wave. In the script, the amplitude is determined by calculating the distance from the center (which is at 4) to the maximum value (which is at 6), resulting in an amplitude of 2.
๐Ÿ’กMedian
The median of a periodic function is the horizontal level about which the function oscillates. In the video, the median is calculated by averaging the maximum and minimum values of the function, which are 6 and 2, respectively. This gives a median of 4, indicating the center point of the oscillation.
๐Ÿ’กGeneral form
The general form of a periodic equation, as discussed in the video, is given by y = a * cos(b * x + c) + d. This formula encompasses the amplitude (a), the frequency (b), the phase shift (c), and the vertical shift (d) of the cosine curve. The script uses this general form to guide the process of finding the specific equation of the given periodic function.
๐Ÿ’กPhase shift
Phase shift in the context of a periodic function refers to the horizontal displacement of the function from its standard position. In the script, the phase shift is represented by the value of 'c' in the general equation. It is determined by observing where the function starts in relation to the origin, with a phase shift of -1 in the given example.
๐Ÿ’กVertical shift
A vertical shift is the upward or downward movement of a function's graph. In the video, the vertical shift is represented by 'd' in the general equation and is found by calculating the distance the function has moved from the x-axis, which is determined to be 4 in the script.
๐Ÿ’กFrequency
Frequency in a periodic function is the number of cycles the function completes in a given interval. It is related to the period of the function. In the script, the frequency is not directly calculated, but the period is determined, which can then be used to find the frequency.
๐Ÿ’กPeriod
The period of a periodic function is the length of one complete cycle of the function. In the video, the period is found by measuring the time it takes for the function to repeat itself, which is determined to be 12 units. This period is then used to calculate the value of 'B' in the general equation.
๐Ÿ’กS curve
An S curve, or sigmoid curve, is another type of periodic function that starts in the middle, moves up to a peak, and then back down to the middle. In the script, it is mentioned as an alternative to the cosine curve for the shape of the graph, but the cosine curve is chosen for the demonstration due to its simplicity.
Highlights

The learning goal is to derive the equation of a periodic function from its graph.

The periodic function could be represented by either an S curve or a cosine curve equation.

The general form of a periodic equation is y = a*cos(Bx + C) + D.

The amplitude (a value) is the distance from the center to the maximum or minimum of the function.

The center (median) of the function is calculated by averaging the maximum and minimum values.

The D value represents the vertical shift of the function from the x-axis.

The amplitude is determined by the difference between the center and the maximum value.

The C value indicates the horizontal shift of the function.

A cosine curve starts at the top and moves down, back, and up to the top again.

An S curve starts from the middle, moves up to the top, comes back, and returns to the middle.

The choice between a cosine curve or an S curve depends on the starting position of the function.

The B value is found using the formula for the period: period = 2ฯ€/B.

The period of the function is the time it takes for the graph to repeat itself.

The period can be measured by the distance between two consecutive peaks or troughs.

Solving for B involves rearranging the period formula and simplifying.

The final equation of the periodic function is y = 2*cos(ฯ€/6*x - 1) + 4.

A systematic approach is used to find the equation from the graph, involving finding D, a, C, and B values.

Transcripts

Browse More Related Video

Writing Equations for Trig Graphs

Precalc 5.5 Day 2 Notes

Trigonometry - Graphing transformations of sin and cos

Writing Equations for Sinusoidal Functions

Writing Equations for Tangent Graphs

Writing Sine and Cosine Equations from Graphs

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Periodic FunctionsMathematicsGraph AnalysisCosine EquationAmplitudeFunction ShiftSystematic MethodEducational ContentTrigonometryGraph Interpretation