Writing Equations for Tangent Graphs
TLDRThis educational script discusses the process of deriving the equation for a tangent graph. It emphasizes starting with identifying the y-intercept, which serves as the midline. The speaker explains how to determine the amplitude by measuring the vertical stretch from the midline to the graph's peak and trough, and how to calculate the period by observing the graph's repetition. The script provides a step-by-step guide to finding the B value, which is the reciprocal of the period, and then combines all these elements to form the equation of the tangent graph. The importance of understanding the graph's features, such as the y-intercept, amplitude, and period, is highlighted to correctly derive the mathematical model.
Takeaways
- 📌 The initial value for a tangent graph is the y-intercept, which is the value at x = 0.
- 📏 The midline of a tangent graph is determined by the y-intercept and is always in the middle of the graph.
- 🔍 Identifying the period of the tangent function is crucial, as it starts and ends at the same point before repeating.
- 📊 The vertical stretch of the tangent graph is found by measuring the distance from the midline to the highest and lowest points on the graph.
- 📐 The B value of the tangent function is calculated by dividing π by the period of the graph.
- 📈 The general form of the tangent function is y = A * tan(Bx) + midline, where A is the vertical stretch, B is the reciprocal of the period, and the midline is the y-intercept.
- 🔢 The amplitude of the tangent function is not directly used in the equation, but the vertical stretch (A value) is.
- 🔄 The tangent function has a flipping action, which can be represented by a negative A value in the equation.
- 🔍 The equation for the tangent graph is constructed by starting with the y-intercept, followed by the vertical stretch, the tangent function itself, and the B value.
- 📝 It's important to note that the period of the tangent function is π, but for the equation, we use the B value which is π divided by the period.
Q & A
What is the first step in finding the equation for a tangent graph?
-The first step is to look for the midline of the graph, which is based on the initial value at y-intercept (the value at x=0).
Why is the y-intercept important when graphing a tangent function?
-The y-intercept is important because it helps establish the midline of the graph, which is a key reference point for the tangent function.
What does the speaker mean by 'vertical stretch' in the context of the tangent graph?
-The 'vertical stretch' refers to the amplitude of the tangent function, which is the distance from the midline to the highest or lowest point of the graph.
How does the period of a tangent function relate to its graph?
-The period of a tangent function is the distance over which the function's graph repeats. It is determined by looking at how the graph starts and ends at the same place before repeating.
What is the significance of the asymptotes in the tangent graph?
-Asymptotes are lines that the graph approaches but never touches. They help in determining the boundaries between which the tangent graph oscillates.
How do you determine the amplitude of the tangent graph from the script?
-The amplitude, or vertical stretch, is determined by the distance from the midline to the highest or lowest point of the graph, which in the script is described as 'half' or 1/2.
What is the period of the tangent function described in the script?
-The period of the tangent function in the script is π/2 (pi over two).
What is the role of the B value in forming the equation of a tangent graph?
-The B value, which is calculated as π divided by the period of the function, determines the frequency of oscillation in the tangent graph's equation.
How is the equation of a tangent graph structured according to the script?
-The equation of a tangent graph is structured as y = A * tan(B * x + C) + D, where A is the amplitude, B is the frequency, C is the phase shift, and D is the vertical shift or midline.
What is the final equation of the tangent graph described in the script?
-The final equation of the tangent graph described in the script is y = -1/2 * tan(2x), with a midline of y = 0.
Why is it not necessary to include the period in the equation of the tangent graph?
-The period is not included in the equation of the tangent graph because the B value, which is derived from the period, is used instead to define the frequency of the function.
Outlines
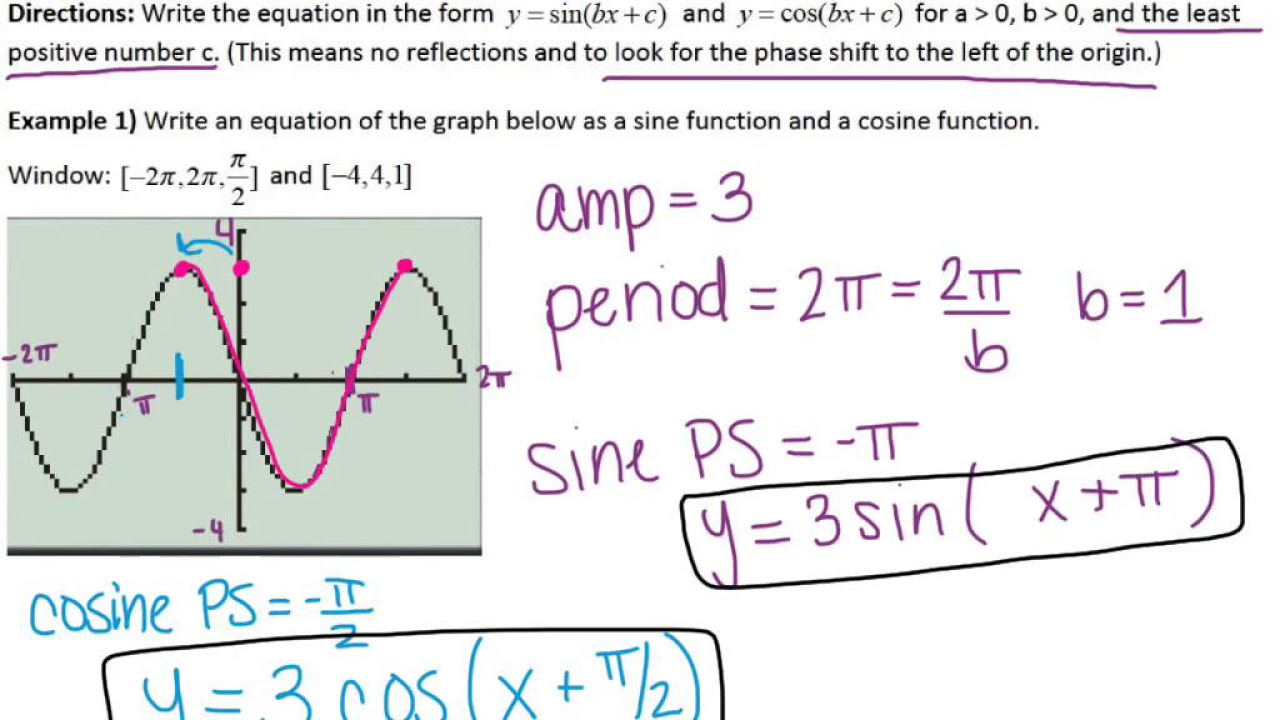
📚 Understanding the Tangent Graph Basics
This paragraph explains the fundamental approach to graphing a tangent function. It starts by identifying the midline, which is based on the initial value or the y-intercept. The speaker emphasizes the importance of the y-intercept in determining the midline of a tangent graph, which is always at the middle of the graph. The period of the tangent function is discussed, and it's noted that it starts and ends at the same place, repeating thereafter. The process involves finding the vertical stretch by measuring the distance from the midline to the highest and lowest points of the graph. The equation for the tangent graph is then constructed using the identified values for the midline, vertical stretch, and period. The equation is expressed in the form y = a * tan(Bx) + midline, where 'a' is the vertical stretch, 'B' is pi divided by the period, and 'x' is the variable.
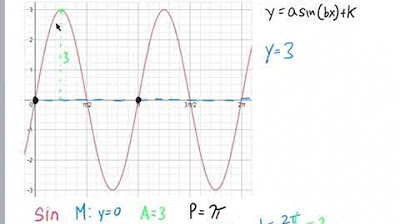
🔍 Constructing the Tangent Function Equation
The second paragraph delves into the specifics of constructing the equation for a tangent graph. It begins by establishing the midline, which in this case is y equals negative 1. The vertical stretch is identified as 2, indicating the height of the graph's peak from the midline. The speaker clarifies that there is no flip in this case, as the graph is ascending normally. The period of the tangent function is given as pi, which is the distance from start to end before it repeats. To form the equation, the value of 'B' is calculated by dividing pi by the period, resulting in B equals 1. The final equation is then written as y equals 2 * tan(1 * theta) - 1, where 'theta' represents the variable. The speaker also mentions that the inclusion of '1 * theta' is not strictly necessary, and alternatives like 'x' or 'f(theta)' can be used.
Mindmap
Keywords
💡Tangent Graph
💡Midline
💡Initial Value
💡Period
💡Asymptotes
💡Amplitude
💡Vertical Stretch
💡B Value
💡Equation
💡Y-Intercept
Highlights
The initial value for a tangent graph is the value at 0, found at the y-axis.
The midline of a tangent graph is determined by the y-intercept.
The period of a tangent graph starts and ends at the same point before repeating.
The end of the period can be identified by the repetition of the graph pattern.
The vertical stretch is determined by the distance between the midline and the graph.
A cosine graph can be visualized by the dots on a tangent graph.
The midline equation for the given graph is y equals 0.
The vertical stretch is half, indicating a downward and upward movement.
The tangent graph has a flip action, which is upside down.
The period of the given tangent graph is π/2.
The B value is calculated as π divided by the period.
The B value for the given graph is 2.
The equation for the tangent graph does not include the period.
The vertical stretch or a value is represented as 1/2 negative.
The equation includes the tangent function multiplied by the B value times x.
The midline is not added at the end of the equation as it is unnecessary.
The final equation for the graph is y = -1/2 * tan(2x).
An alternative tangent equation is y = 2 * tan(x) - 1.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: