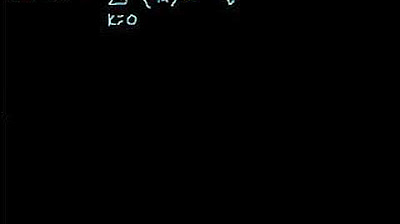Finding the Nth Term in the Binomial Expansion | Binomial Theorem | Pre-Calculus
TLDRIn this video, the instructor demonstrates how to find the nth term in a binomial expansion using the binomial theorem. The process involves understanding the binomial formula, which includes combinations, and factorial calculations. The video provides step-by-step examples for different expressions, showing how to compute specific terms without fully expanding the binomials. Key examples include finding terms in expressions like (x + y)^15, (x - 3y)^20, and (2x - 3)^10. The instructor encourages viewers to leave questions in the comments for further clarification.
Takeaways
- 📚 The video is a tutorial on finding the nth term in a binomial expansion using the binomial theorem.
- 🔢 The binomial theorem formula is presented as \( (x + y)^n = \sum (nCk) \cdot x^{n-k} \cdot y^k \), where \( nCk \) represents the number of combinations of n taken k at a time.
- 📈 The formula for combinations is explained as \( \frac{n!}{k! \cdot (n-k)!} \), which is crucial for calculating the terms in the expansion.
- 📝 The video provides a step-by-step guide on how to apply the binomial theorem to find specific terms in an expansion.
- 📑 The first example demonstrates how to find the fourth term in the expansion of \( (x + y)^{15} \).
- 🔍 The second example shows the process of finding the eighth term in the expansion of \( (x - 3y)^{20} \).
- 📘 The third example illustrates finding the third term in the expansion of \( (2x - 3)^{10} \).
- 📋 Each example includes identifying the value of n (the exponent), k (the term position minus one), and applying the formula to find the term.
- 🧮 The importance of calculating factorials and simplifying expressions is highlighted in the examples.
- 📚 The video concludes with a reminder that understanding the binomial theorem is essential for finding the nth term in binomial expansions.
- 💬 The presenter encourages viewers to ask questions or seek clarifications in the comment section if needed.
Q & A
What is the main topic of the video?
-The main topic of the video is to demonstrate how to find the nth term in binomial expansion using the binomial theorem.
What is the binomial theorem formula used in the video?
-The binomial theorem formula used in the video is (x + y)^n = Σ (n choose k) * x^(n-k) * y^k, where the summation is from k=0 to n.
What does 'n choose k' represent in the binomial theorem?
-'n choose k' represents the number of combinations of n taken k at a time, which is calculated as n! / (k! * (n-k)!).
What is the significance of the term 'k' in the binomial expansion?
-In the binomial expansion, 'k' represents the term number in the expansion, where k=0 represents the first term, k=1 represents the second term, and so on.
How is the first term in the binomial expansion determined?
-The first term in the binomial expansion is determined by x^(n-k) when k=0, which is simply x^n.
Can you provide an example of how to find the fourth term in the expansion of (x + y)^15?
-To find the fourth term in the expansion of (x + y)^15, you would use the formula with n=15 and k=3. The term would be calculated as 15! / (3! * 12!) * x^(15-3) * y^3.
What is the process to find the eighth term in the expansion of (x - 3y)^20?
-To find the eighth term in the expansion of (x - 3y)^20, set n=20 and k=7. The term is calculated as 20! / (7! * 13!) * x^(20-7) * (-3y)^7.
How does the sign of the term change in the binomial expansion?
-The sign of the term changes based on the value of k. For even values of k, the term is positive, and for odd values of k, the term is negative.
What is the significance of the coefficient in the nth term of the binomial expansion?
-The coefficient in the nth term, represented as 'n choose k', determines the weight of each term in the expansion and is crucial for calculating the exact value of the term.
Can the binomial theorem be used for negative exponents?
-The binomial theorem as presented in the video is typically used for non-negative integer exponents. It does not directly apply to negative exponents without modifications.
What is the final step in calculating the value of a specific term in the binomial expansion?
-The final step is to multiply the calculated coefficient (n choose k) by x^(n-k) and y^k, taking into account the sign and any constants like the -3 in the example (x - 3y)^20.
Outlines
📚 Introduction to Binomial Theorem
This paragraph introduces the Binomial Theorem and its application in finding the nth term of a binomial expansion. The presenter explains the formula for binomial expansion, which involves summing the combinations of n taken k times, multiplied by x raised to the power of (n-k) and y raised to the power of k. The formula is further broken down to show the relationship with factorials, emphasizing the combination aspect of the theorem. The video then moves on to an example where the fourth term of (x + y)^15 is calculated using the theorem, illustrating the process step by step.
🔍 Calculating Specific Terms with Binomial Theorem
The second paragraph delves into more examples of using the Binomial Theorem to find specific terms in a binomial expansion. The presenter first calculates the eighth term of (x - 3y)^20, demonstrating the process of identifying the correct term and applying the formula. The calculation involves finding the number of combinations, simplifying factorial expressions, and then combining the results to find the term. The presenter then moves on to another example, calculating the third term of (2x - 3)^10, and explains the steps in a similar manner, showcasing the versatility of the theorem in solving such problems.
🎓 Conclusion and Invitation for Further Engagement
In the final paragraph, the presenter wraps up the video by summarizing the key points covered and expressing hope that the viewers have gained a better understanding of the Binomial Theorem and its application in finding the nth term of a binomial expansion. The presenter invites viewers to ask questions or seek clarifications in the comment section below, encouraging further interaction and learning. The video concludes with a farewell from the presenter, signaling the end of the educational session.
Mindmap
Keywords
💡Binomial Expansion
💡Binomial Theorem
💡Combination
💡Factorial
💡Exponent
💡Term
💡Expansion
💡Coefficient
💡Example
💡Calculation
Highlights
Introduction to finding the nth term in binomial expansion using the binomial theorem.
Explanation of the binomial theorem formula involving combinations and exponents.
Clarification on the role of 'n' as the exponent and 'k' in the binomial expansion.
Demonstration of how to identify the first term (k=0) in the binomial expansion.
Example given to compute the fourth term of (x + y)^15 without full expansion.
Step-by-step guide on applying the formula to find the fourth term in the binomial expansion.
Calculation of the number of combinations for the fourth term using factorials.
Simplification of the factorial expression to find the coefficient of the fourth term.
Illustration of how to raise x and y to their respective powers in the binomial expansion.
Second example presented with (x - 3y)^20 to find the eighth term.
Application of the binomial theorem formula to determine the eighth term's coefficient.
Calculation of the combination for the eighth term and simplification of the expression.
Multiplication of the coefficient with the powers of x and y to find the eighth term.
Third example with (2x - 3)^10 to find the third term.
Detailed steps to calculate the third term's coefficient using combinations.
Final calculation of the third term's value in the binomial expansion.
Conclusion of the video with a summary of the binomial theorem's application.
Invitation for viewers to ask questions or seek clarifications in the comment section.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: