BINOMIAL THEOREM || PRE-CALCULUS

WOW MATH

20 Nov 202127:53

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video lesson focuses on the binomial theorem and its expansion formula. The instructor explains the concept by breaking down the formula into its components and demonstrating its application with examples involving the expansion of (a + b)^n. Step-by-step calculations are shown for various powers of (x + y) and (x - y), highlighting the process of determining coefficients and exponents. The video is designed to help viewers understand the theorem's practical use in mathematics and is capped with an encouragement to like, subscribe, and stay updated for more tutorials.

Takeaways

📚 The video lesson is focused on explaining the Binomial Theorem and its expansion formula.
🔢 The Binomial Theorem formula is presented as (a + b)^n expanded into a sum involving terms of a and b raised to various powers.
📈 The script uses the combination formula nCr (n choose r) to describe the coefficients in the binomial expansion.
👨‍🏫 The instructor provides step-by-step examples to demonstrate how to apply the binomial expansion to specific cases, such as (x + y)^n.
📝 The process involves calculating terms by taking the combination of n taken r, multiplying a to the power of (n-r) and b to the power of r.
🔍 Detailed calculations are shown for the expansion of (8x + 3)^5, breaking down each term's coefficient and powers.
📱 The use of a calculator is recommended for computing the powers and coefficients involved in the expansion.
📉 The script includes an example of expanding (x - 7y)^6, illustrating how to handle negative signs and higher powers.
📚 The lesson covers the full range of terms from the zeroth to the sixth power in the binomial expansion.
👍 The video aims to educate viewers on the application of the binomial theorem in a clear and methodical way.
🔔 The instructor encourages viewers to like, subscribe, and hit the bell button for more math tutorial videos.

Q & A

What is the main topic of the video lesson?
-The main topic of the video lesson is the Binomial Theorem and its expansion.
What is the general formula for binomial expansion?
-The general formula for binomial expansion is (a + b)^n = Σ (n choose r) * a^(n-r) * b^r, where the sum is from r=0 to n.
What does 'n choose r' represent in the binomial expansion formula?
-'n choose r' represents the number of ways to choose r items from n items, which is calculated as n! / (r! * (n-r)!).
How is the first term of the binomial expansion calculated?
-The first term of the binomial expansion is calculated as (n choose 0) * a^n * b^0, which simplifies to a^n since (n choose 0) is 1 and b^0 is also 1.
Can you provide an example of the binomial expansion for (x + y)^2?
-The binomial expansion for (x + y)^2 is x^2 + 2xy + y^2.
What is the process for expanding (8x + 3)^5 using the binomial theorem?
-The process involves identifying 'a' as 8x, 'b' as 3, and 'n' as 5, then applying the binomial expansion formula for each term from r=0 to 5 and summing them up.
How many terms are there in the binomial expansion of (x - 7y)^6?
-There are seven terms in the binomial expansion of (x - 7y)^6, as the expansion goes from r=0 to 6.
What is the significance of the combination formula in binomial expansion?
-The combination formula is used to calculate the coefficients of each term in the binomial expansion, which are represented as 'n choose r'.
Can you explain the term 'binomial coefficient' in the context of the binomial theorem?
-The binomial coefficient refers to the coefficients that multiply the terms in the binomial expansion, which are calculated using the combination formula 'n choose r'.
What is the final expanded form of (8x + 3)^5 according to the video script?
-The final expanded form of (8x + 3)^5 is 32768x^5 + 49152x^4 * 3 + 18270x^3 * 27 + 1094x^2 * 81 + 243x * 243 + 243.

Outlines

00:00

📚 Introduction to Binomial Theorem

This paragraph introduces the concept of the binomial theorem and its expansion formula. The instructor explains the general formula for binomial expansion, which involves the terms 'a' and 'b' raised to the power of 'n', and the coefficients are determined by combinations. The explanation includes an example using 'a' as 'x' and 'b' as 'y', and the process of calculating the expansion for (x + y)^n, where n is the exponent. The instructor also mentions the use of calculators to assist with the calculations.

05:01

🔍 Detailed Binomial Expansion Examples

The second paragraph delves deeper into the binomial expansion with specific examples. It starts with the expansion of (x + y)^2 and (x + y)^3, explaining the process of calculating each term using the binomial coefficients. The instructor then moves on to a more complex example of (8x + 3)^5, breaking down each term of the expansion step by step, including the coefficients and the powers of 'x' and '3'. The use of a calculator is highlighted for performing the necessary arithmetic operations.

10:01

📘 Expanding (8x + 3)^5 Using Binomial Theorem

This paragraph focuses on the detailed expansion of the binomial expression (8x + 3)^5. The instructor systematically goes through each term of the expansion, calculating the coefficients by using the binomial coefficient formula and the powers of '8x' and '3'. The calculations involve various powers of 'x' and '3', and the instructor demonstrates how to use a calculator to find the numerical values of these terms. The final expanded form of the expression is presented.

15:01

📘 Expanding (x - 7y)^6 Using Binomial Theorem

The fourth paragraph presents the binomial expansion of (x - 7y)^6. The instructor outlines the process of finding each term in the expansion, starting with the zeroth term and moving up to the sixth term. Each term's calculation involves the binomial coefficient and the appropriate powers of 'x' and '7y'. The negative signs are handled correctly, and the instructor emphasizes the importance of following the binomial theorem's rules for the expansion.

20:02

🔢 Calculation of Terms in (x - 7y)^6 Expansion

This paragraph continues the detailed calculation of the terms in the expansion of (x - 7y)^6. The instructor provides the numerical values for each term, using a calculator to handle the arithmetic. The calculations include powers of 'x' and '7y', as well as the binomial coefficients. The paragraph emphasizes the step-by-step process of arriving at the final numerical values for each term in the expansion.

25:04

📝 Final Expansion of (x - 7y)^6 and Conclusion

The final paragraph wraps up the expansion of (x - 7y)^6 by presenting the complete list of terms with their calculated values. The instructor adds each term together to give the final expanded form of the binomial expression. The paragraph concludes with a summary of the process and a thank you message to the viewers, encouraging them to like, subscribe, and hit the bell button for more math tutorial videos. The instructor positions themselves as a guide for learning math lessons.

Mindmap

Keywords

💡Binomial Theorem

The Binomial Theorem is a fundamental principle in algebra that provides a way to expand expressions of the form (a + b)^n, where n is a non-negative integer. It is central to the video's theme as it is the main topic being discussed and demonstrated through various examples. The theorem is used to break down and calculate the expanded form of binomial expressions, which is essential for understanding the script's content.

💡Binomial Expansion

Binomial Expansion is the process of multiplying out a binomial expression into its individual terms using the Binomial Theorem. In the video, the concept is illustrated through step-by-step calculations, showing how to apply the theorem to expand expressions like (a + b)^n. The script provides specific examples of binomial expansion, such as (8x + 3)^5, demonstrating the practical application of the theorem.

💡Combination

In the context of the video, a combination refers to a selection of items from a larger set where the order does not matter, and it is used in the binomial expansion formula. The script mentions 'n choose r' which is a binomial coefficient that represents the number of ways to choose r items from a set of n distinct items without regard to the order of selection. This concept is integral to understanding the binomial expansion formula and its application.

💡Exponent

An exponent is a mathematical notation that indicates how many times a number (the base) is multiplied by itself. In the video, exponents are used to denote the power to which a term in the binomial expression is raised, such as in the expression (a + b)^n where n is the exponent. The script explains how to handle exponents in the context of binomial expansion, showing how to calculate terms like a^(n-r) and b^r.

💡Factorial

Factorial, denoted by n!, is the product of all positive integers less than or equal to n. In the video, factorials are used in the calculation of binomial coefficients as part of the binomial expansion formula. The script explains how to use factorials to determine the number of combinations, such as n! / ((n-r)! * r!), which is crucial for understanding the expansion process.

💡Calculator

A calculator is a device or software used to perform mathematical calculations. In the video, the script mentions using a calculator to assist with the computations involved in binomial expansion, such as calculating factorials, powers, and combinations. This suggests that while the theoretical understanding of the binomial theorem is important, practical tools like calculators are also essential for performing the actual calculations.

💡Binomial Coefficient

A binomial coefficient is a positive integer that appears as a coefficient in the binomial expansion. It is represented as 'n choose r' or C(n, r), and it is calculated using the formula n! / ((n-r)! * r!). The video script explains how to calculate binomial coefficients and use them in the expansion formula, which is key to understanding the structure and outcome of binomial expansions.

💡Algebra

Algebra is a branch of mathematics concerning the study of mathematical symbols and the rules for their manipulation. It is the broader field within which the Binomial Theorem and binomial expansion fall. The video script discusses algebraic expressions and their expansion, demonstrating the application of algebraic principles to solve mathematical problems involving binomials.

💡Expression

In mathematics, an expression is a combination of variables, operators, and numbers that can be simplified or evaluated to a single number. The video script frequently refers to 'expressions' in the context of binomials, such as (a + b)^n, which are algebraic expressions that can be expanded using the Binomial Theorem. Understanding expressions is crucial for grasping the concepts taught in the video.

💡Simplification

Simplification in mathematics refers to the process of making a complex expression or equation more straightforward, often by combining like terms or reducing the number of operations. The video script mentions simplification in the context of expanding binomial expressions and then combining the terms to get a simplified form. This process is essential for arriving at the final answer in binomial expansion problems.

Highlights

Introduction to the binomial theorem and its expansion formula.

Explanation of the binomial expansion formula with an example using 'a plus b' raised to 'n'.

Clarification on the terms of the binomial expansion, including the combination formula.

Demonstration of calculating the first term of the binomial expansion for '(x + y)^n'.

Step-by-step calculation of the second term in the binomial expansion.

Expansion of '(x + y)^n' to the third term, illustrating the process with examples.

Continuation to the fourth term of the binomial expansion with detailed calculations.

Illustration of the fifth term calculation in the binomial expansion.

Final term calculation in the binomial expansion for '(x + y)^n'.

Application of the binomial expansion formula to expand '(8x + 3)^5'.

Detailed calculation of each term in the expansion of '(8x + 3)^5'.

Use of a calculator to compute powers and products in the expansion.

Simplification of the expanded form of '(8x + 3)^5'.

Expansion of '(x - 7y)^6' using the binomial theorem.

Calculation of each term in the binomial expansion of '(x - 7y)^6'.

Final simplified form of the binomial expansion for '(x - 7y)^6'.

Conclusion of the video with a summary of the binomial expansion process.

Transcripts

Browse More Related Video

Finding the Nth Term in the Binomial Expansion | Binomial Theorem | Pre-Calculus

ECZ Parabola Paper 1

FINDING THE NTH TERM IN THE BINOMIAL EXPANSION || PRE-CALCULUS

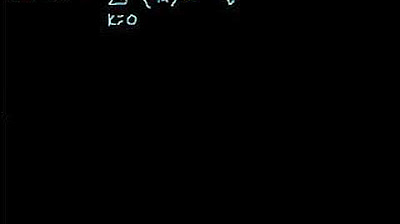
Binomial Theorem (part 1)

17 - Calculating Vector Components in Physics, Part 1 (Component form of a Vector)

First Principles Calculus Grade 12

Related Tags

Binomial Theorem Math Education Formula Expansion Combination Rules Algebra Tutorial Calculus Basics Educational Content Math Lessons Video Tutorial Learning Resource