ECZ Parabola Paper 1
TLDRIn this educational video, the host, Jacob, invites viewers to engage with the content by liking, commenting, and sharing. The session focuses on solving mathematical problems involving a graph, specifically finding the coordinates at points A and B, and determining the minimum value of y at the turning point. Jacob explains the process step-by-step, starting with finding x-intercepts by setting y to zero and solving the quadratic equation. He then demonstrates how to calculate the minimum y-value at the turning point using a formula, breaking down the quadratic equation into its components to find the solution. The host ensures clarity by asking viewers to confirm their understanding and encourages questions throughout the tutorial.
Takeaways
- 📚 The video is an educational session on mathematics, focusing on graph analysis and solving quadratic equations.
- 📈 The host introduces the task of finding coordinates at points A and B on a given graph, which represent x-intercepts.
- 🔍 To find the coordinates, the host suggests setting y to zero and solving the resulting quadratic equation.
- 📝 The quadratic equation provided in the script is y = x^2 - 2x, which is simplified to find the x-intercepts.
- 🎯 The solutions to the equation are x = 0 and x = 2, which correspond to the coordinates of points A and B.
- 📍 Point A is at the origin (0,0), and point B is at (2,0) on the x-axis.
- 🤔 The host checks for understanding and clarity, asking viewers to confirm if they understand the process.
- 📉 The second part of the video involves finding the minimum value of y at the turning point of the graph.
- 📊 The formula for finding the y-value at the turning point is discussed, which involves the coefficients a, b, and c from the quadratic equation.
- 🔢 The host simplifies the formula using the specific coefficients from the equation, resulting in the minimum y-value of -1 at the turning point.
- 👋 The session concludes with the host thanking viewers for joining and signing off.
Q & A
What is the main topic of the video?
-The main topic of the video is solving mathematical problems related to a graph, specifically finding coordinates at points A and B, and determining the minimum value of y at the turning point.
What are the coordinates of point A and B on the graph?
-The coordinates of point A are (0,0) and point B are (2,0), as these are the points where the graph intersects the x-axis.
What method is used to find the x-intercepts on the graph?
-The method used to find the x-intercepts is by setting y equal to zero and solving the resulting quadratic equation.
What is the quadratic equation given in the script?
-The quadratic equation given in the script is y = x(kx - 2), where k is a constant.
How does the script suggest solving the quadratic equation to find the x-intercepts?
-The script suggests setting y to zero and solving for x in the equation y = x(x - 2), which simplifies to x(x - 2) = 0.
What are the values of x obtained from solving the quadratic equation?
-The values of x obtained from solving the equation x(x - 2) = 0 are x = 0 and x = 2.
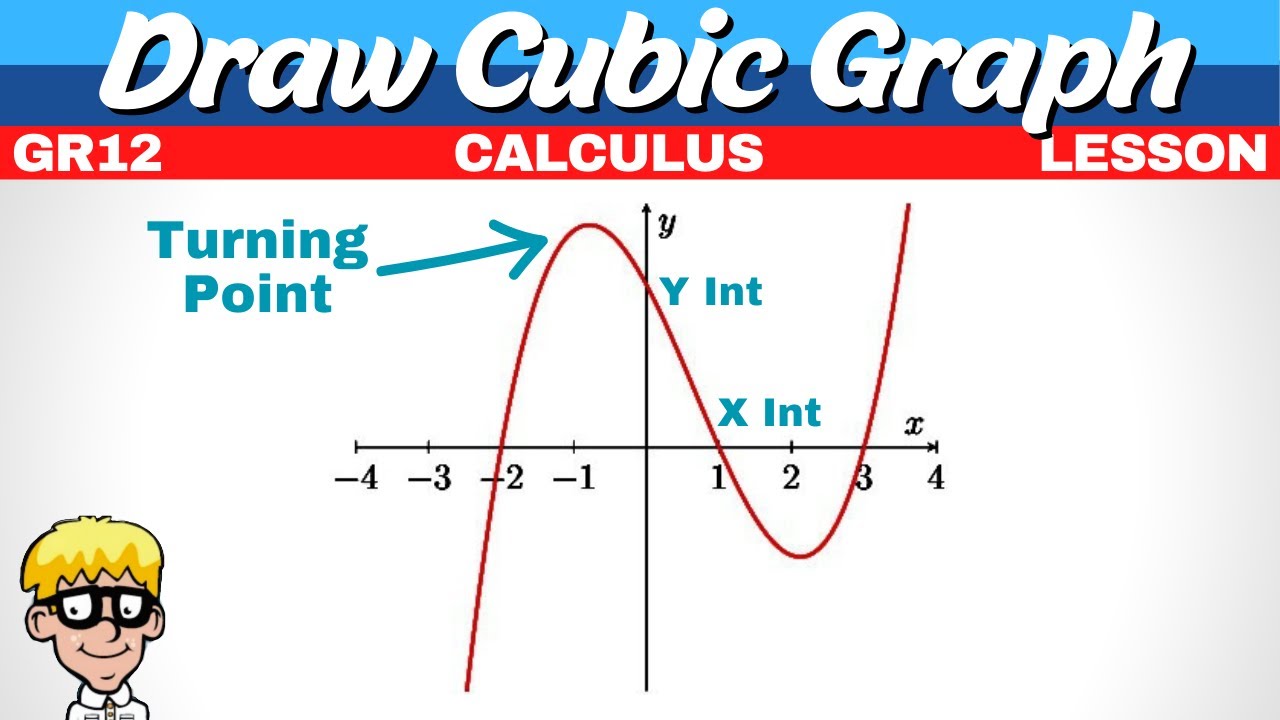
What is the turning point on a graph and how is it related to the minimum value of y?
-The turning point on a graph is the point where the graph changes direction from increasing to decreasing or vice versa. The minimum value of y at the turning point can be found using a specific formula.
What formula is used to find the minimum value of y at the turning point?
-The formula used to find the minimum value of y at the turning point is y = (-b^2)/4a, where a, b, and c are coefficients from the quadratic equation in standard form.
What are the values of a, b, and c in the context of the given quadratic equation?
-In the context of the given quadratic equation y = x(x - 2), a = 1, b = -2, and c = 0.
What is the minimum value of y at the turning point according to the video?
-The minimum value of y at the turning point, according to the video, is -1.
How does the video encourage interaction and engagement from the viewers?
-The video encourages interaction and engagement by asking viewers to like, comment, share, and confirm if the video is clear, and by asking viewers to ask questions if they have any.
Outlines
📚 Introduction to Graph Analysis and Finding Coordinates
The video begins with a prompt for viewers to like, comment, and share. The host, Jacob, introduces the topic of mathematics and specifically graph analysis. The task at hand is to find the coordinates at points A and B on the graph, which represents a quadratic function. Jacob explains that to find these coordinates, one must set the function equal to zero and solve for x, which will give the x-intercepts. The function given is y = x(kx - 2), and by setting y to zero, the x-intercepts are found to be x = 0 and x = 2. These correspond to the points (0,0) and (2,0) on the graph. Jacob ensures that the viewers understand the process and checks for clarity before moving on.
🔍 Detailed Explanation of Finding Coordinates and Minimum Value
In the second paragraph, Jacob continues the explanation on how to find the coordinates of points on a graph by setting y to zero, which leads to solving the quadratic equation. He emphasizes that there will be two solutions for x, which are the x-coordinates of points A and B. Jacob then transitions to the next task, which is to find the minimum value of y at the turning point of the graph. He introduces a formula for finding the y-value at the turning point and explains how to apply it using the coefficients from the quadratic function. By simplifying the formula with the given function, he calculates the minimum y-value to be -1. Jacob ensures that the viewers are following along and invites questions for clarity.
👋 Closing Remarks and Confirmation of Understanding
The final paragraph is a closing segment where Jacob checks in with the viewers to confirm their understanding of the material covered in the video. He seeks confirmation from the audience to ensure that they are okay with the pace and complexity of the information provided. Jacob thanks the viewers for joining the session and bids them farewell, indicating the end of the video.
Mindmap
Keywords
💡Graph
💡Coordinates
💡X-intercept
💡Quadratic Equation
💡Turning Point
💡Minimum Value
💡Formula
💡Standard Form
💡Solve
💡Comment
💡Live
Highlights
Introduction to the mathematics video with an invitation to engage by liking, commenting, and sharing.
The task is to find the coordinates at points A and B on the graph.
Instructions to share the video and invite others who may benefit from the content.
Confirmation request for video clarity and audibility.
Explanation of using x-intercept to find coordinates where the graph cuts the x-axis.
Methodology to set y to zero and solve the resulting quadratic equation for x-intercepts.
Solution for x-intercepts: x equals 0 and x equals 2.
Clarification on the coordinates for points A (0,0) and B (2,0).
Request for audience questions and confirmation of understanding before proceeding.
Emphasis on the process of finding coordinates by setting y to zero and solving the quadratic equation.
Transition to the next question regarding finding the minimum value of y at the turning point.
Introduction of the formula to find the y-value at the turning point of a quadratic graph.
Explanation of how to manipulate the given function to fit the formula for the turning point.
Identification of coefficients a, b, and c from the quadratic equation for use in the formula.
Calculation of the minimum value of y at the turning point as -1.
Summary of steps needed to solve for the turning point and minimum value of y.
Final check for audience understanding and closing of the video session.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: