Descartes Rule of Signs
TLDRThis educational video delves into Descartes' Rule of Signs, a method to estimate the number of positive, negative, and imaginary zeros of a polynomial function. The presenter illustrates the rule with two polynomial examples, demonstrating how to count sign changes to predict zero possibilities. The first example, a cubic polynomial, reveals two positive and one negative real zero, with no imaginary solutions. The second, a quintic polynomial, is shown to have four positive real zeros, one negative, and two imaginary solutions. The video concludes with a practical application of solving the polynomials to confirm the predicted zeros, providing a clear guide on applying Descartes' Rule of Signs.
Takeaways
- 📚 The video focuses on Descartes' Rule of Signs, a mathematical principle used to determine the possible number of positive, negative, and imaginary zeros of a polynomial function.
- 🔍 The rule states that the number of positive real zeros is either equal to the number of sign changes in the polynomial or less than that by a positive even integer.
- 📉 To find the possible number of negative real zeros, the function is evaluated at negative x, and the sign changes are counted similarly.
- 🔢 The total number of zeros for a polynomial is determined by its degree. For example, a third-degree polynomial has three zeros.
- 📝 The video provides a step-by-step example using the polynomial f(x) = x^3 - 2x^2 - x + 2 to illustrate the application of Descartes' Rule of Signs.
- 📉 In the example, it's shown that there are two sign changes for f(x), indicating either two or zero positive real zeros, and one sign change for f(-x), indicating exactly one negative real zero.
- 🔍 The video also demonstrates how to solve the polynomial to confirm the number of zeros and their types, using factoring and synthetic division.
- 📝 A second example is given with the polynomial f(x) = x^5 - 3x^4 + 3x^3 - 9x^2 - 4x + 12 to further illustrate the process.
- 🔢 For the second example, the rule predicts four, two, or zero positive real zeros, and one negative real zero, with the remaining zeros being imaginary.
- 🔎 The video concludes with the actual solving of the second polynomial, revealing two positive real zeros, one negative real zero, and two imaginary zeros, confirming the predictions made by Descartes' Rule of Signs.
- 👍 The video emphasizes the utility of Descartes' Rule of Signs as a preliminary tool to understand the nature of zeros in polynomial functions before solving them.
Q & A
What is Descartes' Rule of Signs used for?
-Descartes' Rule of Signs is used to determine the possible number of positive and negative real zeros of a polynomial function.
How does the rule help with finding the zeros of a polynomial?
-The rule provides an estimate of how many positive and negative real zeros a polynomial might have by counting the sign changes in the polynomial's coefficients.
What is the significance of the total number of zeros for a polynomial with a degree of three?
-For a polynomial with a degree of three, the total number of zeros, including real and imaginary, should be three.
How can you determine the possible number of positive real zeros using Descartes' Rule of Signs?
-You determine the possible number of positive real zeros by counting the sign changes in the polynomial and considering that it could be equal to the number of sign changes or less than a positive even integer.
What is the process for finding the possible number of negative real zeros?
-To find the possible number of negative real zeros, you evaluate the polynomial at negative x, count the sign changes, and apply the same logic as for positive zeros, considering the number of sign changes or less than a positive even integer.
How can you confirm the actual number of zeros using Descartes' Rule of Signs?
-After using the rule to estimate the number of zeros, you can confirm the actual number by solving the polynomial equation to find its roots.
What is the difference between real and imaginary zeros in the context of polynomial functions?
-Real zeros are the solutions to the polynomial where x takes on real number values, while imaginary zeros involve complex numbers where x is a complex number involving the square root of a negative number.
Why can't the number of positive or negative real zeros be negative according to Descartes' Rule of Signs?
-The number of positive or negative real zeros cannot be negative because the rule is based on the count of sign changes, which is inherently a non-negative integer value.
What is the process for solving a polynomial equation after applying Descartes' Rule of Signs?
-After applying Descartes' Rule of Signs, you can solve the polynomial equation by factoring, using synthetic division to find rational zeros, or employing other algebraic methods to find the actual zeros.
How does the video script demonstrate the application of Descartes' Rule of Signs?
-The video script demonstrates the application of Descartes' Rule of Signs by walking through the process of determining the possible number of zeros for two different polynomial functions and then solving those polynomials to confirm the zeros.
What are the limitations of Descartes' Rule of Signs?
-Descartes' Rule of Signs only provides an estimate of the number of positive and negative real zeros and does not account for their exact values or the presence of complex zeros.
Outlines
📚 Descartes' Rule of Signs Introduction
This paragraph introduces Descartes' Rule of Signs, a mathematical theorem that helps predict the number of positive, negative, and imaginary zeros of a polynomial function. The video provides an example polynomial, f(x) = x^3 - 2x^2 - x + 2, and demonstrates how to create a table to categorize the zeros. It explains that the total number of zeros for a cubic polynomial is three and shows how to determine the possible number of positive real zeros by counting sign changes in the polynomial, resulting in either two or zero positive real zeros. The process also involves evaluating the polynomial at negative x to find the number of negative real zeros, which in this case is exactly one. Finally, it deduces that there are no imaginary solutions because the sum of positive and negative real zeros equals the total degree of the polynomial.
🔍 Applying Descartes' Rule to a Fifth Degree Polynomial
The second paragraph delves into applying Descartes' Rule to a higher degree polynomial, f(x) = x^5 - 3x^4 + 3x^3 - 9x^2 - 4x + 12. It outlines the process of creating a table to predict the number of positive, negative, and imaginary zeros, considering the polynomial's degree is five. By counting sign changes in the polynomial, it's determined that there could be four, two, or zero positive real zeros. Similarly, evaluating the polynomial at negative x reveals one possible negative real zero. The paragraph concludes by calculating the number of imaginary solutions, which must add up to complete the total of five zeros, leaving two imaginary solutions. It suggests solving the polynomial to confirm which possibility is correct.
🧩 Solving a Polynomial Using Rational Root Theorem
This paragraph discusses solving the fifth degree polynomial by listing possible rational zeros using the Rational Root Theorem. The factors of the constant term (12) and the leading coefficient (1) are considered as potential zeros. The process begins by testing x = 1 as a zero, which is confirmed through direct substitution. Synthetic division is then used to simplify the polynomial and find additional zeros. The process is repeated with x = -1, leading to a further reduced polynomial. The paragraph concludes with factoring the reduced polynomial by grouping and identifying the remaining zeros, resulting in a completely factored form of the polynomial with two positive real zeros, one negative real zero, and two imaginary solutions.
🎯 Confirming the Correct Zeros for a Polynomial Function
The final paragraph wraps up the video by confirming the correct set of zeros for the original fifth degree polynomial. It reviews the possible combinations of positive, negative, and imaginary zeros and determines which set aligns with the factored form of the polynomial. The conclusion is that the polynomial has two positive real zeros, one negative real zero, and two imaginary solutions, which matches one of the predicted rows from the table. The video ends with a summary of how to use Descartes' Rule to predict the types of zeros a function may have and confirms these predictions by solving for x, encouraging viewers to apply these methods in their mathematical studies.
Mindmap
Keywords
💡Descartes' Rule of Signs
💡Polynomial function
💡Positive zeros
💡Negative zeros
💡Imaginary solutions
💡Sign changes
💡Factoring by grouping
💡Synthetic division
💡Rational zeros
💡Difference of perfect squares
Highlights
Introduction to Descartes' Rule of Signs for determining the zeros of a polynomial function.
Explanation of how to use Descartes' Rule to find the number of positive and negative zeros.
Example provided with the polynomial function f(x) = x^3 - 2x^2 - x + 2.
Creating a table to organize the analysis of positive, negative, and imaginary zeros.
Rule application for determining the number of positive real zeros based on sign changes.
Calculation of possible positive real zeros as either two or zero for the given example.
Process to find the number of negative real zeros by evaluating f(-x).
Conclusion that there is exactly one negative real zero for the example function.
Explanation of how to deduce the number of imaginary zeros based on the total zeros.
Solving the example polynomial to confirm the number of positive, negative, and imaginary zeros.
Factoring the polynomial by grouping to find the zeros.
Result of the example showing two positive real zeros and one negative real zero.
Introduction of a second example polynomial f(x) = x^5 - 3x^4 + 3x^3 - 9x^2 - 4x + 12.
Application of Descartes' Rule to the second example to find possible zeros.
Determination of possible positive and negative real zeros for the second example.
Use of synthetic division to find rational zeros when factoring is not straightforward.
Finding that x = 1 and x = -1 are zeros of the second example polynomial.
Reduction of the polynomial using synthetic division to find remaining zeros.
Final factorization of the second example polynomial and identification of all zeros.
Confirmation of the correct row of zeros for the second example using Descartes' Rule.
Summary of the method to use Descartes' Rule for predicting and confirming zeros of polynomial functions.
Transcripts
Browse More Related Video

Descartes Rule of Signs (Precalculus - College Algebra 33)
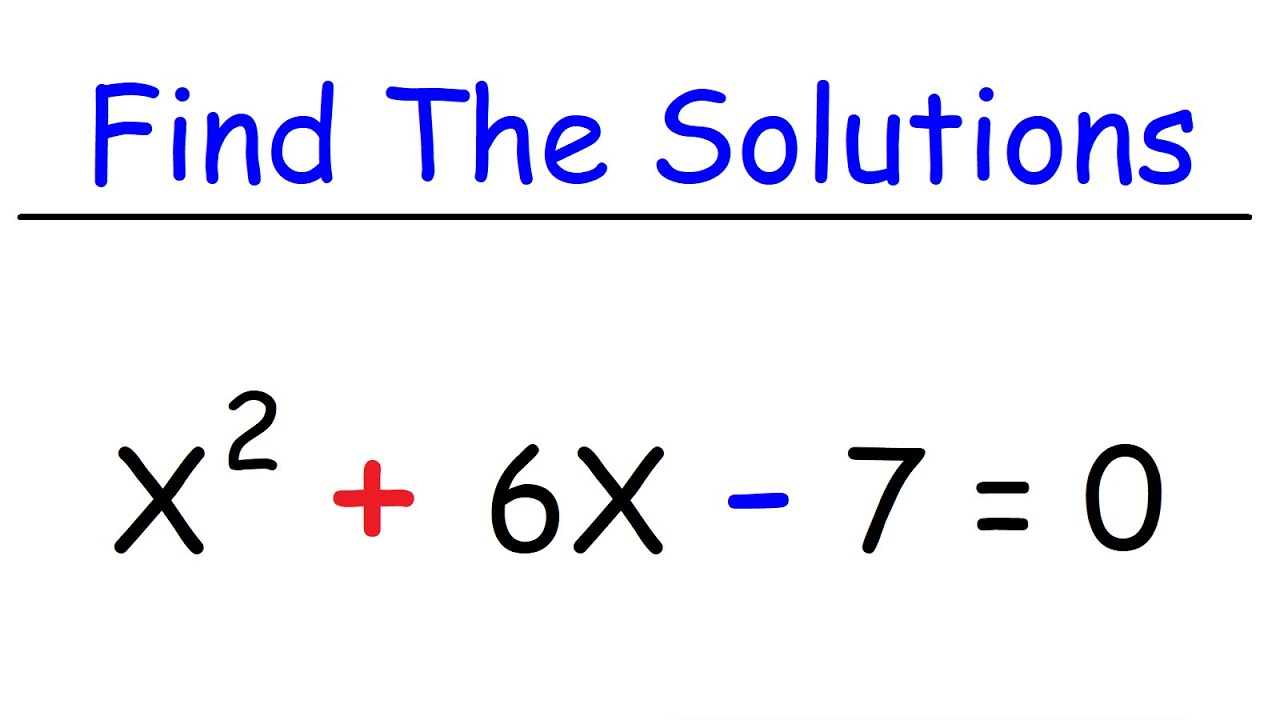
How To Find The Real & Imaginary Solutions of Polynomial Equations
How to Use the Rational Zeros Theorem (Precalculus - College Algebra 34)

Writing Polynomial Functions With Given Zeros | Precalculus

AP Precalculus Practice Exam Question 23

Creating Polynomials from Complex Solutions (Precalculus - College Algebra 36)
5.0 / 5 (0 votes)
Thanks for rating: