How to Use the Rational Zeros Theorem (Precalculus - College Algebra 34)
TLDRThe video script offers an in-depth exploration of the Rational Zeros Theorem, a powerful concept in algebra for finding the roots of polynomial functions. The presenter emphasizes the importance of factoring polynomials and demonstrates how the theorem can predict possible rational zeros, thus simplifying the process of factoring. The script guides viewers through the application of the theorem, including the use of Descartes' Rule of Signs to limit the potential zeros and the synthetic division method for dividing polynomials. The presenter also highlights the limitations of the theorem, such as its inability to account for irrational or complex zeros. The video is structured to first understand the polynomial's order and degree, then apply Descartes' Rule of Signs, followed by the construction of a list of potential rational zeros. Finally, it showcases how to use synthetic division to find actual zeros and factor the polynomial. The script is pedagogical, providing clear examples and stressing the need for practice to master the technique.
Takeaways
- 📚 The Rational Zeros Theorem is a powerful tool for predicting possible rational roots of a polynomial equation, based on the coefficients of the polynomial.
- 🔢 The theorem states that if a polynomial has coefficients a_n, a_(n-1), ..., a_0, the possible rational zeros are of the form p/q, where p is a factor of the constant term a_0, and q is a factor of the leading coefficient a_n.
- 🌟 The Rational Zeros Theorem is particularly useful when combined with other techniques such as Descartes' Rule of Signs, synthetic division, and polynomial factoring.
- 🚫 The theorem has limitations: it does not provide non-rational zeros (like square roots or irrational numbers) and can be tedious if the list of possible zeros is long.
- 🔄 Always attempt to factor the polynomial first, as this can simplify the process of finding zeros and can make the Rational Zeros Theorem more effective.
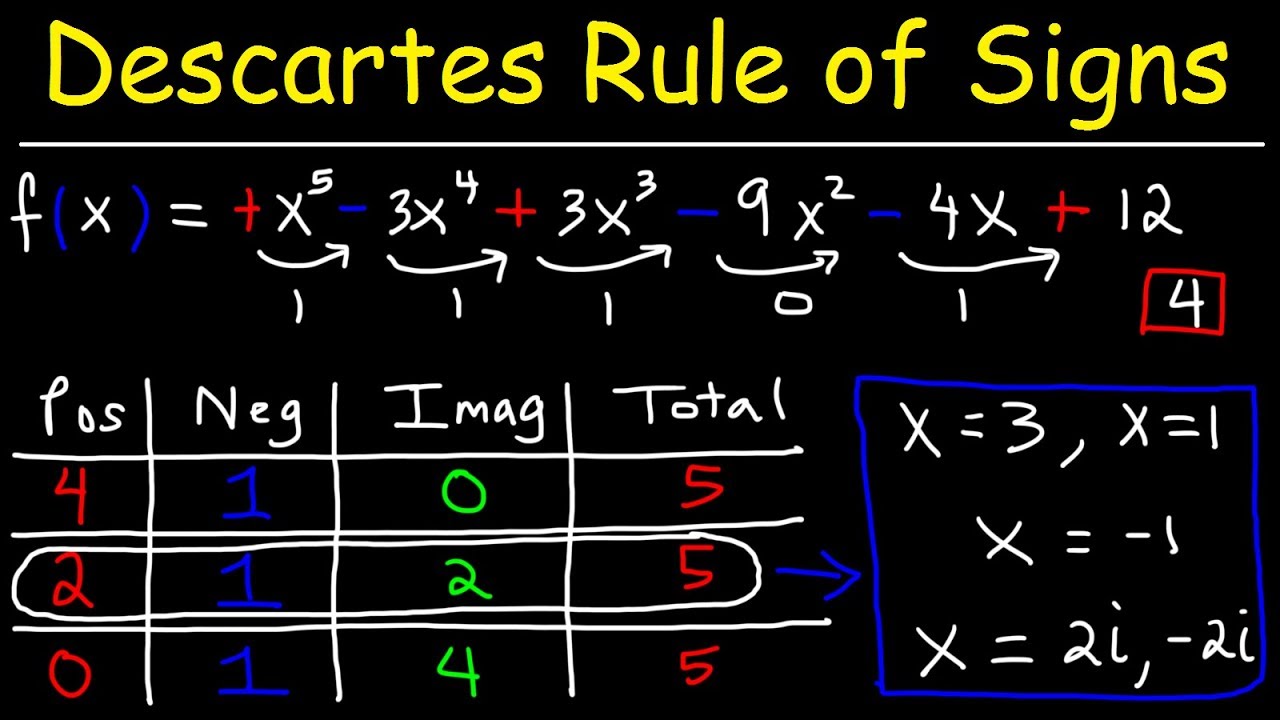
- 📈 Descartes' Rule of Signs can help to quickly determine the number of positive and negative x-intercepts, reducing the list of potential rational zeros.
- 🔢 When using the Rational Zeros Theorem, start by testing the simplest potential zeros (like 1 or -1) and work through the list, eliminating numbers as you find they are not zeros.
- 🔄 If a potential zero divides the polynomial, use synthetic division to further factor the polynomial and find additional zeros.
- 📊 The process of finding zeros can be iterative, requiring multiple applications of synthetic division and checking potential zeros, especially for higher degree polynomials.
- 🎯 The goal of these techniques is to completely factor the polynomial into linear factors and irreducible quadratics, which allows for easy identification of x-intercepts and the graphing of the polynomial function.
Q & A
What is the Rational Zeros Theorem?
-The Rational Zeros Theorem is a method used in algebra to find possible rational solutions to polynomial equations. It states that if a polynomial has rational zeros, then those zeros can be expressed as fractions p/q, where p is a factor of the constant term and q is a factor of the leading coefficient of the polynomial.
Why is the Rational Zeros Theorem useful?
-The Rational Zeros Theorem is useful because it provides a way to find factors of a polynomial without knowing the general form. This is particularly helpful for dividing the polynomial by these factors, which can simplify the polynomial and make it easier to graph, find x-intercepts, and analyze its behavior.
What are the potential drawbacks of using the Rational Zeros Theorem?
-The drawbacks of using the Rational Zeros Theorem include the potential for it to be a tedious process, especially when dealing with a long list of possible zeros. Additionally, it only provides a list of possible rational zeros, so it will not identify irrational zeros, such as square roots or complex numbers.
What is synthetic division and why is it preferred over long division when factoring out linears?
-Synthetic division is a shortcut method used for polynomial division when the divisor is a linear term of the form x - a. It is preferred over long division because it is faster and more efficient, especially when dealing with polynomials of higher degrees.
How does the Descartes' Rule of Signs help in finding the possible number of positive and negative x-intercepts of a polynomial?
-Descartes' Rule of Signs helps to determine the possible number of positive and negative x-intercepts by analyzing the sign changes in the polynomial. The rule states that the number of positive x-intercepts is equal to the number of sign changes when the polynomial is evaluated for positive x, and the number of negative x-intercepts is the number of sign changes when evaluated for negative x, with the possibility of subtracting 2 if there are irreducible quadratic factors.
What is the importance of factoring a polynomial before applying the Rational Zeros Theorem?
-Factoring a polynomial before applying the Rational Zeros Theorem is important because it can simplify the process of finding zeros. If a polynomial can be factored, it means that the polynomial can be broken down into simpler parts, which can then be individually analyzed for zeros. This can save time and effort, especially if the polynomial has a general form that allows for easy factoring.
What is the role of the leading term and constant term in determining the possible rational zeros of a polynomial?
-The leading term and constant term of a polynomial play a crucial role in determining the possible rational zeros. The factors of the constant term and the leading coefficient are used to create a list of potential rational zeros (p/q), where p is a factor of the constant term and q is a factor of the leading coefficient.
How does the degree of a polynomial affect the maximum number of x-intercepts it can have?
-The degree of a polynomial directly affects the maximum number of x-intercepts it can have. A polynomial of degree n can have at most n x-intercepts. This is because each root of the polynomial corresponds to an x-intercept, and the fundamental theorem of algebra guarantees that a polynomial of degree n has n roots, which may be real or complex.
What is the significance of the remainder theorem in the context of finding zeros of a polynomial?
-The remainder theorem states that if a polynomial is divided by a binomial of the form x - a, the remainder of the division is the value of the polynomial at x = a. If the remainder is zero, it means that x = a is a root of the polynomial, and thus, x - a is a factor of the polynomial. This is significant for finding zeros as it provides a method to identify potential x-intercepts.
How does the process of synthetic division help in factoring a polynomial after finding a rational zero?
-Synthetic division is a method used to divide a polynomial by a linear factor (x - a) after a rational zero has been identified. It simplifies the polynomial by reducing its degree by one and provides the quotient, which is a new polynomial that can be further analyzed for additional zeros. This process can be repeated until the polynomial is completely factored into linear factors and irreducible quadratics.
What is the significance of the multiplicity of a root in the context of the Rational Zeros Theorem?
-The multiplicity of a root refers to the number of times a particular root appears in the factored form of a polynomial. When using the Rational Zeros Theorem, if a rational zero is found, it must be checked again because it could have a multiplicity greater than one. This means the root could be a repeated root, leading to factors like (x - a)^2 or higher powers, which would not be identified if the zero was only checked once.
Outlines
📚 Introduction to the Rational Zeros Theorem
The speaker introduces the Rational Zeros Theorem, a powerful concept in the course, and emphasizes its utility in factoring polynomials without a general form. The theorem allows for the identification of possible rational x-intercepts for a function, given the coefficients of an ordered polynomial. The speaker acknowledges the theorem's pros, such as providing factors without explicit factorization, and cons, like its tedious nature and limitation to rational zeros, excluding square roots and complex zeros.
📈 Applying the Rational Zeros Theorem
The speaker explains the process of applying the Rational Zeros Theorem by identifying factors of the constant term and the leading coefficient. By creating a list of possible rational zeros through the permutations of these factors, one can predict potential x-intercepts. The speaker also discusses the importance of factoring out x first if possible, and the goal to completely factor the polynomial to find x-intercepts and graph the function effectively.
🔢 Factoring and Rational Zeros Theorem Example
The speaker provides a detailed example of applying the Rational Zeros Theorem to a cubic polynomial. They discuss the importance of recognizing the polynomial's order, degree, and end behavior. By evaluating the function for positive and negative x, the speaker demonstrates how to use Descartes' Rule to predict the number of positive and negative x-intercepts. The speaker then illustrates the process of finding rational zeros by dividing factors of the constant term by factors of the leading coefficient.
🔍 Checking Work and Factoring Out Linears
The speaker emphasizes the importance of checking one's work when applying the Rational Zeros Theorem. They explain that if a number evaluates to zero, it is an x-intercept and creates a factor. The speaker then demonstrates how to use synthetic division to divide the polynomial by the identified factor, resulting in a new polynomial that is easier to handle. They also discuss the possibility of finding repeated roots and the need to factor the remaining polynomial completely.
📊 Factoring Quadratics and Complex Solutions
The speaker discusses the limitations of the Rational Zeros Theorem when dealing with quadratics that are not factorable or contain complex solutions. They explain that while the theorem can provide a starting point, one may need to use factorization or the quadratic formula to fully solve for x-intercepts in such cases. The speaker also highlights the importance of understanding the difference between factoring and using the quadratic formula to handle reducible and irreducible quadratics.
🎯 Comprehensive Factoring and Rational Zeros
The speaker wraps up the discussion by reiterating the importance of factoring before applying the Rational Zeros Theorem. They present a final example, demonstrating how to use Descartes' Rule of Signs and the Rational Zeros Theorem to identify x-intercepts and factor the polynomial. The speaker also shows how the choice of factors can impact the ease of factoring and the final form of the factored polynomial. They conclude by reinforcing the comprehensive nature of the techniques learned, which allow for the complete factoring of polynomials and the determination of x-intercepts.
Mindmap
Keywords
💡Rational Zeros Theorem
💡Synthetic Division
💡Polynomial Functions
💡Descartes' Rule of Signs
💡Factoring
💡End Behavior
💡X-Intercepts
💡Degree of a Polynomial
💡Long Division
💡Quadratic Formula
Highlights
Introduction to the Rational Zeros Theorem, a powerful tool for finding the factors of polynomials without knowing the general form.
Emphasis on the utility of the theorem as a culmination of concepts like Descartes' Rule of Signs, long division, and synthetic division.
Explanation of how the theorem allows for the creation of a list of possible rational x-intercepts for a function.
Discussion on the pros and cons of using the Rational Zeros Theorem, including the potential tediousness of checking a long list of numbers.
The importance of always attempting to factor out x or another factor first, especially when a constant term is present.
Demonstration of the process to find factors of the constant term and the leading coefficient to generate a list of possible fractions.
Use of Descartes' Rule of Signs to save work by determining the possible number of positive and negative x-intercepts.
Procedure for evaluating potential x-intercepts starting with the smallest numbers and using the Remainder Theorem.
Technique of synthetic division as a faster method for dividing polynomials after finding a linear factor.
The concept of multiplicity in roots and how repeated roots can lead to higher degree factors like x^2 - 1 being factorable.
Strategy to completely factor a polynomial into linears or irreducible quadratics for full analysis.
Illustration of the process with examples, showing how to handle polynomials of different degrees and factorability.
Caution against relying solely on the list of possible rational zeros, as it does not include irrational or complex zeros.
The quadratic formula as an alternative method to find zeros when the list of rational zeros is exhausted or not applicable.
Importance of checking for repeated factors when a number evaluates to zero, indicating a potential multiple root.
Final example demonstrating the entire process, including factoring by grouping and dealing with irreducible quadratics.
Highlighting the flexibility in choosing factors and the impact on subsequent factorability and ease of the process.
Conclusion on the comprehensive understanding required for polynomials, including graphing, factoring, and finding x-intercepts.
Transcripts
Browse More Related Video

Synthetic Division and Long Division of Polynomials (Precalculus - College Algebra 32)

Finding ALL Solutions of Polynomials (Precalculus - College Algebra 37)

Solving Polynomial Equations By Factoring and Using Synthetic Division

Finding All Zeros of a Polynomial Function Using The Rational Zero Theorem

Factoring Cubic Polynomials- Algebra 2 & Precalculus
Descartes Rule of Signs
5.0 / 5 (0 votes)
Thanks for rating: