Descartes Rule of Signs (Precalculus - College Algebra 33)
TLDRThe video introduces Descartes' Rule of Signs, a mathematical concept that helps predict the number of positive and negative x-intercepts of a polynomial function. By counting sign changes and evaluating the function for negative x, one can determine the potential number of intercepts on each side of the x-axis. This rule is particularly useful when combined with the Rational Zeros Theorem for solving polynomial functions and can significantly save time by eliminating unnecessary calculations.
Takeaways
- 📚 The Descartes' Rule of Signs is a useful concept that helps predict the number of positive and negative x-intercepts of a polynomial function without solving it.
- ✅ The rule states that the number of positive x-intercepts is equal to the number of sign changes in the polynomial's coefficients or less by an even number.
- 🔍 When evaluating for negative x-intercepts, changing the signs of the odd exponent terms helps determine the potential number of negative x-intercepts.
- 🚫 If there are no sign changes after evaluating for negative x, it guarantees zero negative x-intercepts for the polynomial.
- 🔢 The degree of a polynomial indicates the maximum number of x-intercepts it can have, which could be reduced by irreducible quadratics.
- 📉 Irreducible quadratics contribute to the degree of a polynomial but do not result in additional x-intercepts, thus subtracting two from the degree count.
- 🤝 The Descartes' Rule of Signs is particularly powerful when combined with the Rational Zeros Theorem, as it can significantly reduce the number of potential zeros to check.
- ⛔ The rule ensures that if a polynomial has an odd degree, it must have at least one real x-intercept, and if it has an even degree, it may or may not have any.
- 🔗 Understanding the interplay between the degree of a polynomial, the Descartes' Rule of Signs, and the concept of irreducible quadratics is crucial for efficiently solving polynomial equations.
- 📈 The rule helps in systematically narrowing down the potential x-intercepts, thus saving time and effort in solving polynomial functions.
- 📚 The Descartes' Rule of Signs is a fundamental tool that will be frequently referenced in further studies of polynomial functions and their solutions.
Q & A
What is Descartes' Rule of Signs used for in the context of the video?
-Descartes' Rule of Signs is used to determine the possible number of positive and negative real roots of a polynomial function, which can save time by avoiding unnecessary checks of values that would not be x-intercepts.
How does the rule help in solving rational functions?
-The rule provides a preliminary count of the possible positive and negative x-intercepts, which can be used in conjunction with the Rational Zeros Theorem to narrow down the potential zeros of the function.
What is the significance of the number of sign changes in a polynomial?
-The number of sign changes from left to right in a polynomial indicates the potential number of positive x-intercepts. An even number less than the count of sign changes also represents possible x-intercepts.
Why do we change the signs of odd exponents when evaluating for negative x?
-Changing the signs of odd exponent terms when evaluating for negative x helps to determine the potential number of negative x-intercepts without actually performing the complex calculation of substituting negative x into the polynomial.
How does the degree of a polynomial relate to the maximum number of x-intercepts it can have?
-The degree of a polynomial represents the maximum total number of x-intercepts it can have, which includes both real and complex solutions. If the degree is odd, the polynomial must have at least one real x-intercept.
What does it mean if there are no sign changes when evaluating a polynomial for negative x?
-If there are no sign changes when evaluating a polynomial for negative x, it indicates that there are zero negative x-intercepts for the polynomial.
Why do we subtract an even number from the count of sign changes when determining the number of x-intercepts?
-Subtracting an even number accounts for irreducible quadratics in the polynomial, which do not contribute additional x-intercepts but reduce the degree of the polynomial by two.
How does the rule help in factoring polynomials?
-By identifying the possible number of positive and negative x-intercepts, the rule helps to focus on the relevant factors of the polynomial, reducing the number of potential factors to check and thus making the factoring process more efficient.
What is the practical application of knowing the number of positive and negative x-intercepts before applying the Rational Zeros Theorem?
-Knowing the number of x-intercepts allows for a more strategic approach to the Rational Zeros Theorem, as it eliminates the need to check values that cannot be zeros of the polynomial, thus saving time and effort.
Why is it important to have the polynomial in order before applying the rule of signs?
-Having the polynomial in order ensures that the sign changes are counted accurately, as the order of terms affects the sign of each term. This is crucial for the correct application of Descartes' Rule of Signs.
What does the absence of positive x-intercepts imply for the graph of the polynomial?
-If a polynomial has zero positive x-intercepts, the graph of the polynomial will not intersect the positive half of the x-axis.
How can the rule of signs help in understanding the relationship between the degree of a polynomial and its x-intercepts?
-The rule of signs, along with the knowledge of the polynomial's degree, helps to establish the maximum possible number of x-intercepts and provides insight into the distribution of these intercepts across the real number line.
Outlines
📘 Introduction to Descartes' Rule of Signs
The video begins with an introduction to a concept known as Descartes' Rule of Signs, which is a useful tool for predicting the number of positive real roots of a polynomial equation. The host emphasizes the rule's utility in saving time when solving rational functions and polynomial functions using the Rational Zeros Theorem. The explanation focuses on the importance of factoring and the zero product property in solving polynomial equations. The video promises to delve into the specifics of the rule and its implications for polynomial factoring.
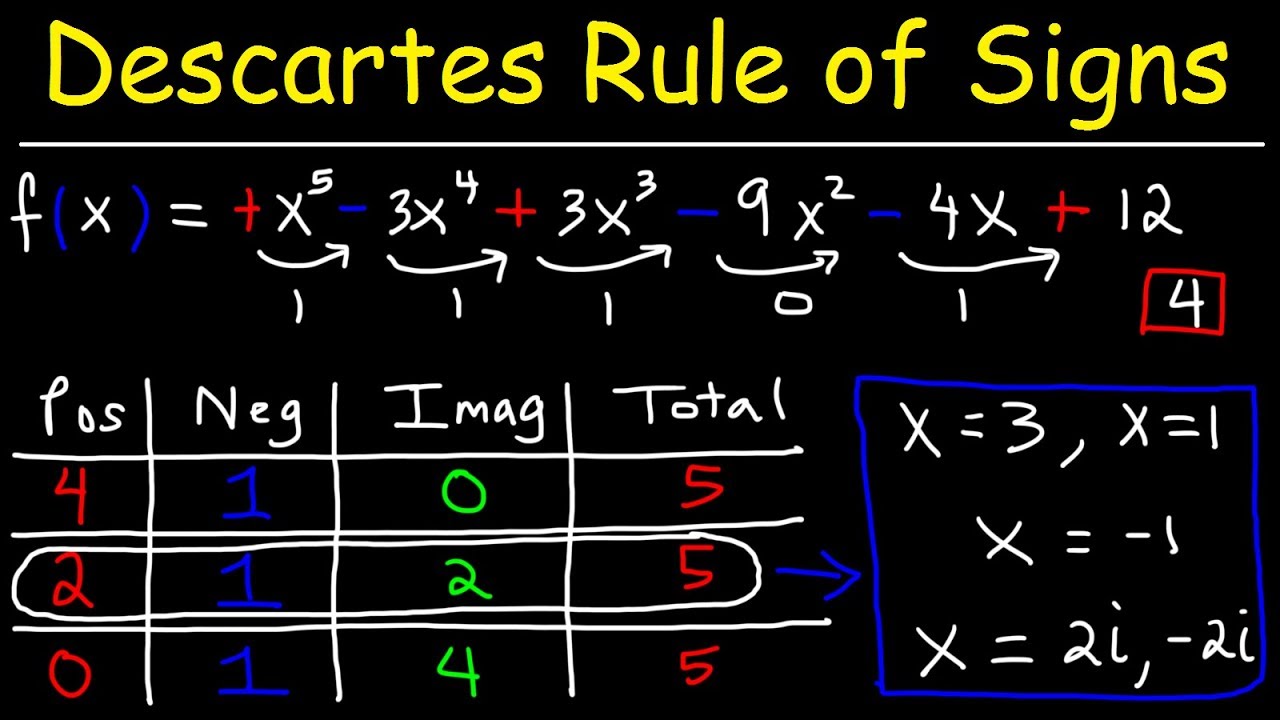
🔢 Applying Descartes' Rule of Signs
The host explains how to apply Descartes' Rule of Signs by counting the number of sign changes in a polynomial to determine the potential number of positive x-intercepts. The explanation includes the rationale behind subtracting even numbers from the count of sign changes to account for irreducible quadratics. The video also clarifies that the degree of a polynomial represents the maximum number of x-intercepts and how the rule of signs can help eliminate unnecessary checks for x-intercepts that do not exist.
🤔 Evaluating for Negative X and Odd Exponents
The video moves on to discuss how to determine the number of potential negative x-intercepts by evaluating the polynomial for negative x. The host provides a trick to simplify this process: changing the signs of odd-powered terms without actually plugging in negative x. The explanation highlights the significance of this step in conjunction with the Rational Zeros Theorem for efficiently finding zeros of a polynomial.
🔍 Understanding the Implications of Degree and Intercepts
The host delves into the relationship between the degree of a polynomial, the concept of irreducible quadratics, and how they affect the total number of x-intercepts. It is explained that if a polynomial does not have the maximum number of intercepts suggested by its degree, the missing intercepts are accounted for by irreducible quadratics or complex solutions that come in pairs. The video emphasizes the importance of this understanding for factoring polynomials.
📐 Demonstrating Descartes' Rule of Signs with Examples
The video provides examples to illustrate the application of Descartes' Rule of Signs. It is shown how to count sign changes for both positive and negative x-intercepts and how to adjust for odd-powered terms when evaluating negative x. The examples demonstrate how the rule can predict the number of x-intercepts and guide the factoring process, including identifying irreducible quadratics.
📉 Examining a Polynomial with No Positive X-Intercepts
The host examines a specific polynomial example, h(x), which is already in order, and applies Descartes' Rule of Signs to show that there are no positive x-intercepts. By evaluating h(-x), it is determined that there could be either two or zero negative x-intercepts. The video connects this analysis to the concept of odd-degree polynomials, which must cross the x-axis at least once, and the implications for the total number of x-intercepts based on the polynomial's degree.
🔗 Connecting Descartes' Rule of Signs to Future Topics
The video concludes with a reminder of the importance of Descartes' Rule of Signs in upcoming lessons, particularly in conjunction with the Rational Zeros Theorem. The host encourages viewers to rewatch the section if necessary to fully grasp the concept and its applications. The video sets the stage for further exploration of polynomial solutions and the efficient use of the rule of signs in solving mathematical problems.
Mindmap
Keywords
💡Descartes' Rule of Signs
💡Rational Zeros Theorem
💡Polynomial Functions
💡X-Intercepts
💡Irreducible Quadratics
💡Zero Product Property
💡Degree of a Polynomial
💡Sign Changes
💡Factoring
💡Synthetic Division
💡Complex Solutions
Highlights
Descartes' Rule of Signs is a useful concept that can save time when solving polynomial functions.
The rule helps to predict the number of positive and negative x-intercepts of a polynomial graph.
The number of sign changes from left to right in a polynomial equation indicates the possible number of positive x-intercepts.
Subtracting an even number from the count of sign changes helps account for irreducible quadratics.
Changing the signs of odd exponents and evaluating for negative x can predict the number of negative x-intercepts.
The degree of a polynomial represents the maximum number of x-intercepts it can have.
Irreducible quadratics do not contribute to additional x-intercepts but reduce the degree count.
The rule of signs can eliminate unnecessary checks, saving time in calculations.
If a polynomial has no sign changes when evaluated for negative x, it guarantees zero negative x-intercepts.
The rule of signs is particularly powerful when combined with the Rational Zeros Theorem.
The video provides a step-by-step guide on how to apply Descartes' Rule of Signs to polynomial functions.
Understanding the interplay between degree, sign changes, and irreducible quadratics is crucial for applying the rule effectively.
The video emphasizes the importance of having the polynomial in order before applying the rule.
The presenter uses multiple examples to illustrate the application of Descartes' Rule of Signs.
The rule helps in determining the potential number of x-intercepts without actual computation.
The video concludes with the application of the rule to a sixth-degree polynomial, demonstrating its practical use.
Descartes' Rule of Signs is a fundamental concept that will be referenced in subsequent videos on polynomial solving.
Transcripts
Browse More Related Video
Descartes Rule of Signs

Creating Polynomials from Real Zeros (Precalculus - College Algebra 30)

Synthetic Division and Long Division of Polynomials (Precalculus - College Algebra 32)
How to Use the Rational Zeros Theorem (Precalculus - College Algebra 34)

AP Precalculus Practice Exam Question 23

Finding All Zeros of a Polynomial Function Using The Rational Zero Theorem
5.0 / 5 (0 votes)
Thanks for rating: