THE DERIVATIVE OF A SQUARE ROOT

MATHStorya
24 Feb 202104:50
EducationalLearning
32 Likes 10 Comments

TLDRThe video script is an in-depth exploration of derivatives, focusing on finding the derivatives of functions involving square roots. It begins by introducing the concept of a solid substrate 'k' and the derivative of a square root function 'y = √u', explaining that the derivative 'y' is 'u' prime over 2 times the square root of 'u'. The script then applies this formula to various functions, such as 'y = √(3x + 4)' and 'y = √(4x^2 - 2x + 5)', demonstrating how to calculate 'u' prime and subsequently the derivative 'y' prime for each case. It also covers the simplification of expressions and the application of the distributive property, as seen in the example 'u = 3x - 2 * x^2 + 2x'. The script concludes with the derivative of a more complex function 'u = 3x^3 + 4x^2 - 4x', showcasing the process of finding 'u' prime and the final derivative. This comprehensive guide is an engaging and informative resource for understanding the calculus of square root functions.

Takeaways
  • 📚 To find the derivative of a square root function, use the formula y' = u' / (2 * sqrt(u)), where u is the variable inside the square root.
  • 🔍 When differentiating y = sqrt(3x + 4), identify u = 3x + 4 and its derivative u' = 3, then apply the formula to get y' = 3 / (2 * sqrt(3x + 4)).
  • 📈 For y = sqrt(4x^2 - 2x + 5), set u = 4x^2 - 2x + 5, find u' = 8x - 2, and use the formula to find y' = (8x - 2) / (2 * sqrt(4x^2 - 2x + 5)).
  • ✅ Factor out constants in the denominator for simplification, as done with y' = (4x - 1) / sqrt(4x^2 - 2x + 5) after canceling out the 2 in the numerator and denominator.
  • 🔢 For the function u = (3x - 2) * (x^2 + 2x), apply the distributive property to simplify it to u = 3x^3 + 6x^2 - 2x^2 - 4x before differentiating.
  • 🧮 Differentiate u to get u' = 9x^2 + 8x - 4, then use it in the square root derivative formula to find y' for the corresponding y involving u.
  • 🛠️ When differentiating a composite function, identify the inner function (u) and its derivative (u'), then apply the chain rule.
  • 📉 The derivative of a constant is zero, which simplifies the differentiation process by eliminating constants when finding u'.
  • 🤔 Consider the power of x when differentiating terms like x^n, where the derivative involves multiplying by the power and reducing it by 1.
  • 🧬 For the term 3x^3, the derivative is found by multiplying the coefficient (3) by the power of the x (3) to get 9x^2, following the power rule.
  • 🔄 The process of differentiating involves understanding the structure of the function, applying the correct rules, and simplifying the result.
Q & A

  • What is the general formula to find the derivative of a square root function?

    -The general formula to find the derivative of a square root function y = √u is y' = (u' * √u) / 2, where u' is the derivative of u with respect to x.

  • How do you find the derivative of y = √(3x + 4)?

    -To find the derivative of y = √(3x + 4), first identify u = 3x + 4. The derivative u' is 3. Then apply the general formula to get y' = (3 / 2) * √(3x + 4).

  • What is the derivative of y = √(4x^2 - 2x + 5)?

    -For y = √(4x^2 - 2x + 5), the derivative u' of u = 4x^2 - 2x + 5 is 8x - 2. The derivative y' is then (8x - 2) / (2 * √(4x^2 - 2x + 5)) which simplifies to (4x - 1) / √(4x^2 - 2x + 5).

  • How do you simplify the expression for the derivative of y = √(3x - 2) * x^2 + 2x?

    -First, distribute to get u = 3x^3 + 6x^2 - 4x. Then find u' = 9x^2 + 12x - 4. The derivative y' is (9x^2 + 12x - 4) / (2 * √(3x^3 + 6x^2 - 4x)).

  • What is the derivative of a constant?

    -The derivative of a constant is always zero because a constant does not change with respect to the variable.

  • Why do we divide by 2 in the general formula for the derivative of a square root function?

    -The factor of 2 in the denominator comes from the chain rule, where we have to multiply by the derivative of the inner function (√u) which is 1/(2√u).

  • What is the process to find the derivative of the function y = √(3x - 2) * x^2 + 2x?

    -First, simplify the function to get u = 3x^3 + 6x^2 - 4x. Then find the derivative u' of u. Finally, apply the general formula for the derivative of a square root function with the found u' and u.

  • How do you find the derivative of the term 4x^2 in the function u = 4x^2 - 2x + 5?

    -The derivative of 4x^2 with respect to x is found by using the power rule, which gives 4 * 2x or 8x.

  • What is the derivative of x^n with respect to x?

    -The derivative of x^n with respect to x, where n is a constant, is given by the power rule as n * x^(n-1).

  • What is the role of the chain rule in differentiating composite functions like square roots of polynomials?

    -The chain rule is used to differentiate composite functions by differentiating the outer function (in this case, the square root) and then multiplying by the derivative of the inner function (the polynomial).

  • Why is the derivative of a term like 3x to the power of 3 expressed as 3 * 3x^2?

    -The derivative of 3x to the power of 3 is found by applying the power rule to x^3, resulting in 3 * 3x^2. The constant 3 is multiplied through because the derivative of a constant times a variable is the constant times the derivative of the variable.

  • What is the significance of the distributive property in simplifying expressions before differentiation?

    -The distributive property is used to simplify expressions by multiplying terms and combining like terms, which makes it easier to apply differentiation rules and find the derivative of more complex functions.

Outlines
00:00
📚 Derivative of a Square Root Function

This paragraph explains the process of finding the derivative of a square root function. It begins by introducing the concept with a generic function y = √u and its derivative y' = u' / (2√u). The explanation then applies this formula to specific examples: y = √(3x + 4), where u = 3x + 4, and the derivative u' is calculated as 3. Substituting this into the formula yields y' = 3 / (2√(3x + 4)). The paragraph continues with another example, y = √(4x^2 - 2x + 5), calculating u' as 8x - 2, and the derivative y' as (8x - 2) / (2√(4x^2 - 2x + 5)). The process simplifies to y' = 4x - 1 / √(4x^2 - 2x + 5). The paragraph concludes with a third example, simplifying the expression 3x * x^2 + 2x * 3x - 2x^2 - 4x to 3x^3 + 4x^2 - 4x, and then finding its derivative u' = 9x^2 + 8x - 4. Finally, the derivative y' is calculated as (9x^2 + 8x - 4) / (2√(3x^3 + 4x^2 - 4x)).

Mindmap
Keywords
💡Derivative
The derivative is a fundamental concept in calculus that represents the rate at which a function changes at a certain point. In the video, the derivative is used to find the rate of change of different functions, which is central to understanding how these functions behave. For example, the script mentions finding the derivative of y = √(u), where u is a function of x.
💡Square Root
A square root is a value that, when multiplied by itself, gives the original number. In the context of the video, square roots are used within functions, such as y = √(u), to demonstrate how to find their derivatives. The script uses square roots to illustrate the process of differentiation.
💡Solid Substrate
While the term 'solid substrate' is mentioned at the beginning of the transcript, it does not appear to be directly related to the mathematical content discussed in the video. It might be a metaphor or an unrelated term. The video focuses on mathematical functions and their derivatives, not on physical substrates.
💡U-Substitution
U-substitution is a technique used in calculus to simplify the process of finding derivatives of complex functions. The video uses this method by setting u equal to an expression involving x, differentiating that expression to find u', and then using it to find the derivative of the original function. For instance, when the function y = √(3x + 4) is given, u is set to 3x + 4 to simplify the derivative calculation.
💡Differentiation Formula
A differentiation formula is a mathematical rule used to find the derivative of a function. The video presents a specific formula for differentiating square root functions, which is y' = u' / (2√u). This formula is repeatedly applied throughout the video to find the derivatives of various functions.
💡Chain Rule
The chain rule is a fundamental rule in calculus for differentiating compositions of functions. Although not explicitly named in the transcript, the method of differentiating u and then using it to find the derivative of y in terms of x implies the use of the chain rule. It is central to the process of finding the derivatives in the video.
💡Distributive Property
The distributive property is a basic algebraic principle that allows for the simplification of expressions. In the video, it is used to simplify the expression for u before differentiating. For example, when u = 3x * x^2 + 2x * x - 2x^2 - 4x, the distributive property is applied to combine like terms, resulting in u = 3x^3 + 4x^2 - 4x.
💡Constant
In calculus, a constant is a value that does not change with respect to the variable being considered. The derivative of a constant is always zero, which is a key point mentioned in the video when differentiating functions that include constant terms, such as y = √(3x + 4) where the constant '4' has a derivative of zero.
💡Power Function
A power function is a function of the form u = x^n, where n is a constant. The video deals with power functions when differentiating expressions like u = 3x^3 + 4x^2 - 4x. The derivatives of these power functions are found using the power rule, which is a special case of the general differentiation rules.
💡Combining Like Terms
Combining like terms is an algebraic process used to simplify expressions by adding or subtracting terms that have the same variable raised to the same power. In the video, this process is used to simplify complex expressions for u before applying differentiation rules, such as when simplifying u = 3x^3 + 6x^2 - 2x^2 - 4x to u = 3x^3 + 4x^2 - 4x.
💡Factoring
Factoring is a mathematical technique used to break down an expression into a product of simpler expressions. In the video, factoring is used to simplify the derivative of y = √(4x^2 - 2x + 5) by factoring out a common factor of 2 from the numerator of the derivative, resulting in a simplified expression for y'.
Highlights

Deriving the square root of a function involves a specific formula: y' = u' / (2 * sqrt(u))

To find the derivative of y = sqrt(3x + 4), first identify u = 3x + 4, then apply the formula to get y' = 3 / (2 * sqrt(3x + 4))

The derivative of a constant is zero, which simplifies the calculation of u'

For y = sqrt(4x^2 - 2x + 5), u = 4x^2 - 2x + 5, and the derivative y' is found by applying the formula and simplifying

Factoring out constants from the numerator can simplify the derivative expression, as shown in the example with y = sqrt(4x^2 - 2x + 5)

The distributive property is used to simplify expressions before differentiating

When simplifying expressions, like terms are combined to create a more manageable derivative

The derivative of a polynomial term involves multiplying the coefficient by the power of x and then decreasing the power by one

The derivative of x to a power is found by multiplying the exponent by the coefficient and then reducing the exponent by one

The derivative of a squared term is twice the term times its derivative

For u = 3x^3 + 6x^2 - 4x, the derivative u' is calculated by applying the power rule and combining like terms

Substituting the derivative of u into the square root derivative formula yields y' for the given function

The final derivative expression is simplified by canceling out common factors

Each step in the derivative process is crucial for accurately finding the derivative of a square root function

Understanding the derivative of constants and variables separately is key to combining them in more complex functions

The process demonstrates the application of calculus rules to find derivatives of composite functions involving square roots

The method shown can be generalized for finding derivatives of square root functions with different algebraic expressions inside the root

The transcript provides a clear, step-by-step approach to finding derivatives, which is valuable for educational purposes

The use of algebraic manipulation and simplification techniques is emphasized in the process of finding derivatives

Transcripts

Browse More Related Video

DERIVATIVE OF RADICAL: THE CHAIN RULE

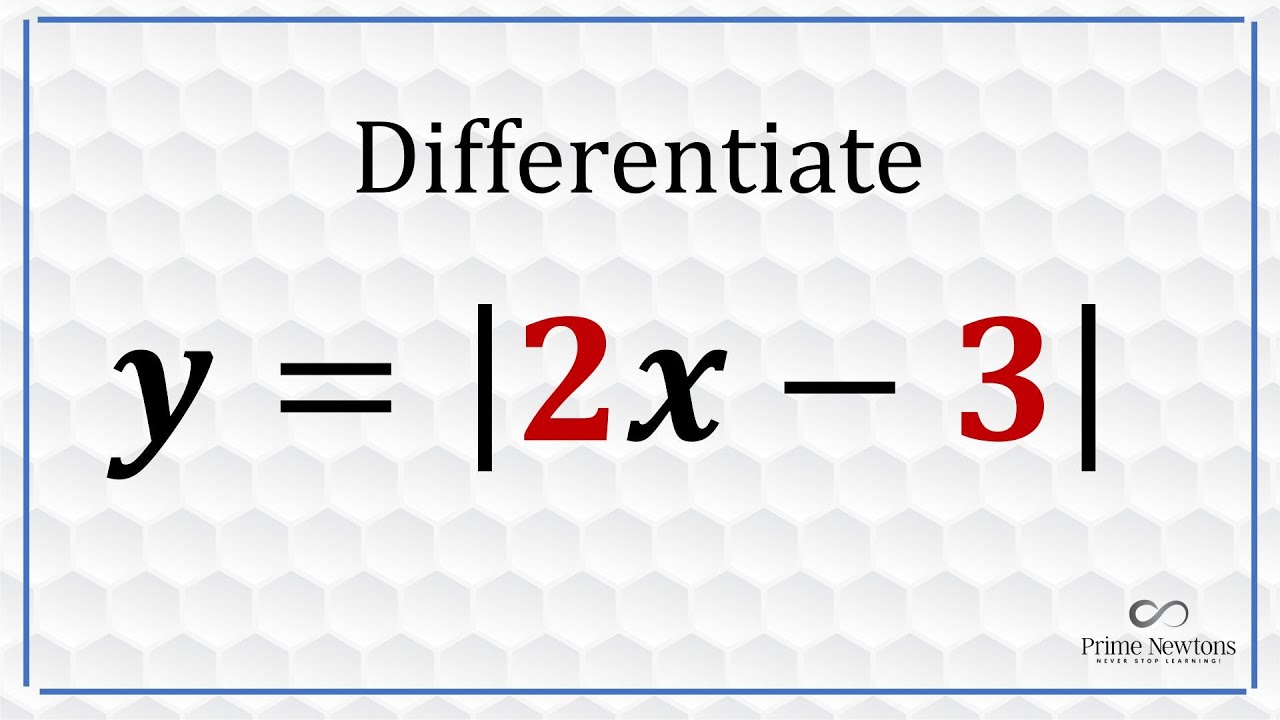
Derivative of absolute value function

Derivatives of Exponential Functions

Derivatives of Inverse Trigonometric Functions

Trig functions differentiation | Derivative rules | AP Calculus AB | Khan Academy

Integration of Rational Functions By Completing The Square - Calculus

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
DerivativesSquare RootMathematicsCalculusFunction AnalysisRoot DerivationSimplificationDifferential CalculusMathematical ProcessEducational ContentSTEM Field