angular velocity: what is it and how is it calculated
TLDRIn this engaging video from 'High School Physics Explained,' Paul introduces viewers to the fundamental concepts of rotational mechanics. He begins by addressing the limitations of linear displacement and velocity when describing circular motion, such as the zero displacement after a complete 360-degree rotation and the dependency of velocity on the radius. To overcome these issues, he delves into angular measurements, highlighting the importance of the number pi and its relation to the circumference and diameter of a circle. Paul then defines the radian as the SI unit for angular measurement and explains its relationship to a complete revolution, which is 2 pi radians. The video continues by establishing the connection between angular velocity (Ω), linear velocity (v), and the radius (r), demonstrating that v equals Ω times r. He also touches on centripetal acceleration, which is the acceleration directed towards the center of the circular path. Throughout the video, Paul emphasizes the vector nature of angular velocity and uses the right-hand rule to determine its direction. This comprehensive introduction to angular motion lays the groundwork for further exploration into rotational physics, including torque, moment of inertia, and angular momentum.
Takeaways
- 🔄 **Centripetal Acceleration**: An object moving in a circle experiences centripetal acceleration directed towards the center of the circle.
- 🎢 **Tangential Velocity**: The velocity of an object in circular motion is always tangent to the circle at the object's current position.
- ⭕ **Displacement in Circular Motion**: After a full 360-degree rotation, the displacement is zero because the object returns to its starting point.
- 📏 **Relationship Between Radius and Velocity**: An increase in the radius of the circle results in an increase in the linear velocity of the object.
- 📐 **Measuring Angles**: Angles are typically measured in degrees, with a full circle being 360 degrees.
- 🤔 **Origin of 360 Degrees**: The choice of 360 degrees for a full circle is arbitrary and may have originated from the Babylonian numerical system based on 60.
- 🅿️ **Pi (π)**: Pi is a constant representing the ratio of a circle's circumference to its diameter, approximately equal to 3.14 or 22/7.
- 🌀 **Radians**: Radians are the SI unit for measuring angles, where one radian is the angle subtended at the center of a circle by an arc whose length is equal to the radius.
- ↻ **Complete Revolution in Radians**: A full loop or revolution is equivalent to 2π radians, making it the basis for angular measurements.
- 📐 **Angular Displacement (θ)**: In rotational motion, we use θ to represent the angle in radians.
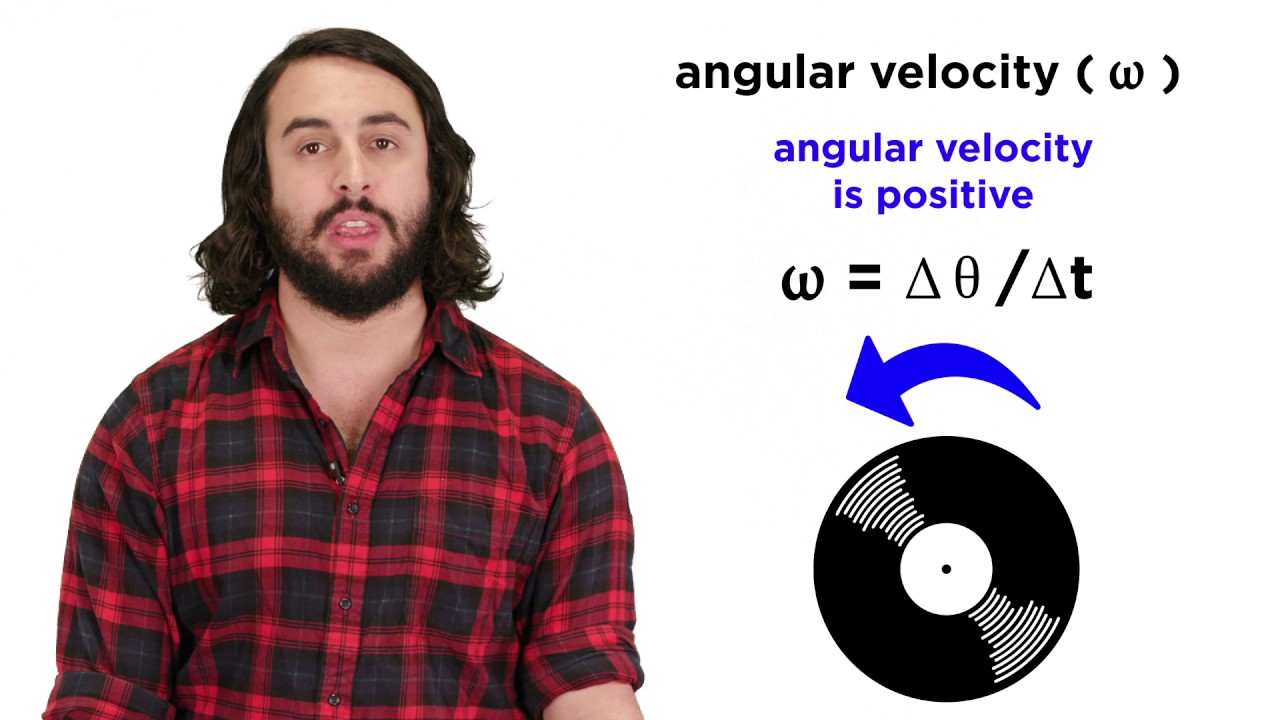
- ⏱️ **Angular Velocity (ω)**: Angular velocity is the rate of change of the angle with respect to time, symbolized by ω and measured in radians per second.
- ⏰ **Period and Frequency**: The period (T) is the time taken for one complete cycle, and the frequency (f) is the number of cycles per unit time, related by f = 1/T.
- 🔄 **Direction of Angular Velocity**: The direction of angular velocity is established using the right-hand rule, where the thumb points in the direction of the velocity when the fingers curl in the direction of rotation.
Q & A
What is the main focus of the video?
-The video focuses on an introduction to rotational mechanics, discussing concepts such as angular displacement, velocity, and acceleration in the context of circular motion.
Why is centripetal acceleration considered when discussing circular motion?
-Centripetal acceleration is considered because it is the acceleration that an object experiences when moving in a circular path, always directed towards the center of the circle.
What is the significance of the number pi in the context of circular motion?
-The number pi (approximately 3.14) represents the ratio of a circle's circumference to its diameter, which is crucial for calculating the circumference (πd) and relating it to the radius (2πr) in formulas.
How is angular velocity different from linear velocity?
-Angular velocity (symbolized by Omega, Ω) is the rate of change of the angle with respect to time, whereas linear velocity is the rate of change of displacement with respect to time. Angular velocity is associated with rotational motion, while linear velocity is associated with straight-line motion.
What is the SI unit for measuring angles in the context of rotational motion?
-The SI unit for measuring angles in rotational motion is the Radian, which is defined as the angle subtended at the center of a circle by an arc whose length is equal to the radius of the circle.
How is the direction of angular velocity determined?
-The direction of angular velocity is determined using the right-hand rule, where if you curl the fingers of your right hand in the direction of rotation, your thumb points in the direction of the angular velocity vector.
What is the relationship between angular velocity and linear velocity at a point on a rotating object?
-The linear velocity at any point on a rotating object is equal to the angular velocity multiplied by the radius of rotation. This means that as the radius increases, the linear velocity at that point also increases, assuming the angular velocity remains constant.
What is the formula for centripetal acceleration in terms of angular velocity and radius?
-The formula for centripetal acceleration is given by a_c = Ω^2 r, where a_c is the centripetal acceleration, Ω is the angular velocity, and r is the radius of the circular path.
Why is it necessary to consider radians instead of degrees when discussing rotational motion?
-Radians are necessary because they provide a direct relationship between the angle of rotation and the arc length, which is essential for accurate mathematical descriptions and calculations in rotational motion.
How does the period of rotation relate to angular velocity?
-The period of rotation (T) is the time taken for one complete revolution, and it is the inverse of the frequency (f). Angular velocity (Ω) is related to the period by the formula Ω = 2π/T or Ω = 2πf.
What is the right-hand rule, and how is it used in physics?
-The right-hand rule is a common mnemonic used to determine the direction of vectors associated with rotation, such as angular velocity. It states that if you point the fingers of your right hand in the direction of rotation, your thumb will point in the direction of the vector.
Outlines
📚 Introduction to Rotational Mechanics
The first paragraph introduces the topic of rotational mechanics, focusing on the motion in a rotational frame. It discusses the limitations of linear displacement and velocity when applied to circular motion, such as the issue of displacement being zero after a complete 360-degree turn. The paragraph also explains the concept of centripetal acceleration, which is the inward acceleration experienced by an object moving in a circle. To better analyze circular motion, the script transitions into a discussion about measuring angles, the significance of the number pi, and the relationship between a circle's circumference and its diameter. The concept of a radian as an SI unit for measuring angles is introduced, and the relationship between a complete revolution and radians is established.
🌀 Angular Displacement, Velocity, and Acceleration
The second paragraph delves into the specifics of angular displacement, velocity, and acceleration. It begins by defining the symbols used for these quantities in rotational motion: theta (θ) for angular displacement, omega (ω) for angular velocity, and alpha (α) for angular acceleration. The paragraph then explores the relationship between linear and angular velocity, showing that linear velocity is the product of angular velocity and radius. The concept of centripetal acceleration is also revisited, with its formula derived from the relationship between velocity, radius, and acceleration. The paragraph concludes by highlighting the importance of understanding these variables for further study in rotational dynamics, including the transition from force to torque and mass to moment of inertia.
↻ Direction of Angular Velocity Using the Right-Hand Rule
The third and final paragraph addresses the direction of angular velocity and displacement. It clarifies that direction is not described using terms like clockwise or anti-clockwise, but rather by the axis of rotation and the right-hand rule. This rule involves curling the fingers of the right hand in the direction of rotation, with the thumb pointing in the direction of the angular velocity vector. The paragraph emphasizes the counterintuitive nature of this convention but stresses its importance for understanding advanced concepts such as torque, precession, and angular momentum. The video concludes with a call to action for viewers to engage with the content through likes, shares, subscriptions, and comments, and to support the creator via Patreon for continued educational content.
Mindmap
Keywords
💡Rotational Mechanics
💡Centripetal Acceleration
💡Velocity
💡Angular Displacement
💡Radians
💡Pi (π)
💡Angular Velocity (Ω)
💡Acceleration
💡Centripetal Force
💡Right-Hand Rule
💡Moment of Inertia
💡Angular Momentum
Highlights
Introduction to rotational mechanics, focusing on motion in a rotational frame.
Circular motion involves centripetal acceleration directed inward towards the center of the circle.
Linear velocity is tangential to the motion, but its magnitude increases with the radius.
Displacement in circular motion is a challenge since it returns to zero after a full circle.
Degrees are used to measure angles, but the choice of 360 degrees is arbitrary.
Pi (π) is a constant ratio of a circle's circumference to its diameter.
The circumference of a circle is given by the formula πD or 2πR.
Radians are the SI unit for measuring angles, defined as the angle subtended at the center of a circle by an arc whose length is equal to the radius.
A full revolution is equivalent to 2π radians.
Half a revolution is π radians, and a quarter revolution is π/2 radians.
Linear displacement (s) in rotation is replaced by angular displacement (θ) measured in radians.
Angular velocity (ω) is the rate of change of the angle with respect to time.
The relationship between linear velocity (v) and angular velocity (ω) is v = ωR.
Centripetal acceleration is given by the formula v²/R, which can be expressed as ω²R when substituting v with ωR.
Angular velocity is a vector quantity, with its direction determined by the right-hand rule.
Understanding the direction of angular velocity is crucial for topics like torque, precession, and angular momentum.
The video concludes with a teaser for upcoming lessons on rotational variables such as torque, moment of inertia, and angular momentum.
The importance of supporting the channel via Patreon to continue creating high-quality physics education content.
Transcripts
Browse More Related Video

Rotational Motion: An Explanation, Angular Displacement, Velocity and Acceleration

Rotational Motion Physics, Basic Introduction, Angular Velocity & Tangential Acceleration

Pure Rolling Motion | Physics with Professor Matt Anderson | M12-12
Angular Motion and Torque
Circular Motion: Acceleration (Angular, Tangential, Centripetal)

Relating angular and regular motion variables | Physics | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: