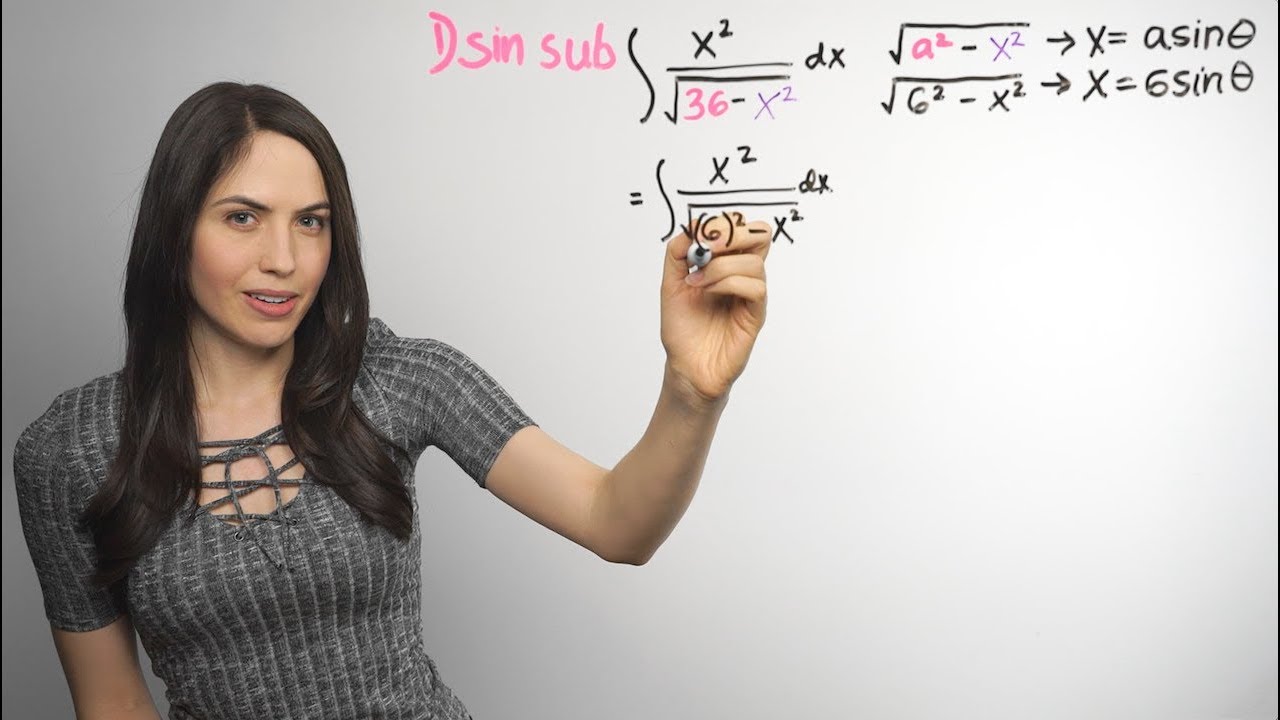[LIVE] zoom Math Calculus For Business | Integrals by substitution #byparts #partialfractionmethod

mathmontrealmath
15 Apr 202005:08
EducationalLearning
32 Likes 10 Comments

TLDRThe video script appears to be a tutorial on solving mathematical problems involving radicals and integrals. The speaker guides the audience through a step-by-step process, starting with simplifying expressions with radicals and then moving on to integration techniques. They emphasize the importance of correctly identifying the base of the radical and simplifying the expression before integrating. The tutorial covers the substitution method using 'u' as a variable to represent the base of the radical, transforming the problem into a more manageable form. The speaker also discusses different strategies for simplifying fractions and the application of integration rules. The session concludes with the speaker showing how to revert back to the original variable 'X' after performing the integration, and the need to present the final answer in its simplest form. The script is instructional and seems aimed at individuals practicing advanced algebra or calculus.

Takeaways
  • 📚 **Understanding the Problem**: The speaker emphasizes the importance of recognizing the structure of the problem before proceeding with any mathematical operations.
  • 🔍 **Identifying the Radical**: The base of the radical is crucial; it should be identified correctly to ensure the correct approach to solving the problem.
  • 🔢 **Substitution with 'u'**: Introduce a new variable 'u' to simplify the expression, particularly when dealing with radicals and complex terms.
  • 🧩 **Breaking Down Expressions**: When faced with complex expressions, it can be helpful to break them down into simpler components for easier manipulation.
  • 🔄 **Simplification Techniques**: The speaker discusses two methods of simplification: splitting the fraction or pushing the radical up, and the choice depends on the problem at hand.
  • 📉 **Integration Rules**: Knowing the basic integration rules, such as the integral of x^n and 1/x, is fundamental for solving integral calculus problems.
  • 🔀 **Applying Integral Rules**: The application of integral rules is contingent upon the simplification of the expression, which should be done prior to integration.
  • 🧷 **Substitution Back to 'x'**: After solving the integral in terms of 'u', it's necessary to substitute back to the original variable 'x' to find the final solution.
  • ⚖️ **Simplified Final Answer**: The final answer should be simplified, ensuring that any constants or coefficients are correctly adjusted (e.g., flipping 3/2 to 2/3).
  • 📈 **Dealing with Complex Scenarios**: The script provides a methodical approach to tackling complex calculus problems, which is valuable for practicing and understanding harder scenarios.
  • 🔗 **Connecting Back to the Original Expression**: The process of solving should always loop back to the original problem's context, ensuring that the solution is relevant and makes sense in the given scenario.
Q & A

  • What is the general approach when dealing with expressions involving radicals?

    -The approach involves simplifying the expression by taking the radical of the base expression, usually all but two of the terms inside the radical, and then solving for the variable in question.

  • What does 'u' represent in the context of the script?

    -'u' is used as a substitution for a more complex expression, such as 'X - 4', to simplify the integration process.

  • How does the script suggest to handle the integration of expressions with radicals?

    -The script suggests first simplifying the expression by using substitution and then applying the appropriate integration rules.

  • What is the significance of the phrase 'push the radical'?

    -The phrase 'push the radical' refers to the process of moving the radical term outside of the integral sign to simplify the expression before integration.

  • What are the two methods mentioned for simplifying expressions?

    -The two methods mentioned are breaking the fraction into separate terms (splitting) and pushing the radical outside of the fraction (pushing).

  • How does one determine the value of 'u' in the given scenario?

    -In the given scenario, 'u' is determined by the base of the radical, which is 'X - 4'.

  • What is the rule for integrating a function of the form 1/x?

    -The rule for integrating a function of the form 1/x is the natural logarithm of the absolute value of x, denoted as ln|x|.

  • What does the script imply about the importance of simplification before integrating?

    -The script emphasizes that simplification is crucial before integrating, as it allows for the application of integral rules and makes the integration process more manageable.

  • What is the process of 'flipping' the fraction mentioned in the script?

    -The process of 'flipping' the fraction involves taking the reciprocal of the fraction to simplify the expression, such as changing 1/2 to 2/1.

  • Why is it necessary to plug 'X' back into the final expression after using substitution?

    -Plugging 'X' back into the final expression after using substitution is necessary to return to the original variable of the problem and to express the final solution in terms of the original variable.

  • What is the final step in the integration process as described in the script?

    -The final step is to simplify the expression to its most reduced form, ensuring that the answer is in its simplest terms before filling in the final answer.

  • How does the script differentiate between different scenarios in integration?

    -The script differentiates by discussing the use of substitution and the importance of recognizing when to split terms or push radicals, depending on the complexity of the expression.

Outlines
00:00
🧮 Complex Integration Techniques

This paragraph delves into the intricacies of mathematical integration, specifically focusing on the handling of radicals and powers within integral expressions. The speaker introduces the concept of substitution, using 'u' as a replacement for a more complex part of the integral, such as 'X - 4'. The narrative unfolds with a detailed discussion on when and how to apply substitution, and the importance of recognizing the base of the radical. The paragraph emphasizes the challenges of keeping track of the variable after substitution and the need for simplification. It also touches on different methods of simplification, such as splitting fractions or pushing radicals up. The summary concludes with the integration of 'u' and the subsequent steps to simplify and solve the integral, highlighting the need for a careful approach to ensure the final answer is correctly simplified.

05:00
📐 Substitution in Integration

The second paragraph continues the mathematical theme by focusing on the technique of substitution in integration, particularly emphasizing the selection of the substitution variable 'u'. It hints at the process of setting 'u' equal to a power base, which is a crucial step in transforming the integral into a more manageable form. Although the paragraph is brief and somewhat truncated, it underscores the importance of correctly identifying the substitution variable as a key part of solving complex integral calculus problems. The paragraph suggests that the choice of 'u' can significantly simplify the integration process and improve the efficiency of solving the problem at hand.

Mindmap
Keywords
💡powers
In the context of the video, 'powers' likely refers to the mathematical concept of exponents, where a number is multiplied by itself a certain number of times. This is a fundamental operation in algebra and calculus, and it is used to manipulate expressions and solve equations. For example, the script mentions 'some with powers,' indicating the presence of exponents in the mathematical expressions being discussed.
💡push
The term 'push' in the video script is used to describe the process of moving terms within an equation to a different side to simplify or solve it. This is a common technique in algebra, and it is often used to isolate variables or to prepare an equation for integration or differentiation. The script uses the phrase 'some you should push' to illustrate the strategy of moving terms around in an equation.
💡radicals
Radicals, specifically square roots or other roots, are a mathematical concept where a number is raised to the power of 1/n. In the video, 'radicals' are mentioned in relation to simplifying expressions under a radical sign. The script discusses the process of 'pushing' the radical up or simplifying expressions involving radicals, which is a common step in calculus when dealing with integrals.
💡integral
An 'integral' in calculus is a mathematical concept that represents the area under a curve, defined by a function, over an interval. The script discusses the process of integrating expressions, which involves finding the antiderivative of a function. This is a core concept in calculus and is used to solve problems involving accumulation, such as finding the distance traveled by an object given its acceleration.
💡simplify
Simplification is the process of making a mathematical expression easier to understand or work with by reducing it to its simplest form. In the video, 'simplify' is mentioned in the context of preparing expressions for integration and dealing with fractions and radicals. Simplification is a crucial step in solving mathematical problems as it often makes the problem more manageable and easier to solve.
💡splitting
In the context of the video, 'splitting' refers to the method of breaking down a complex fraction or expression into simpler parts to make it easier to integrate or solve. The script mentions 'splitting' as a preferred method for simplifying fractions, which is a common technique used in calculus to deal with complex integrals.
💡u-substitution
U-substitution is a technique used in calculus to simplify integrals that are difficult to evaluate directly. It involves replacing a part of the integral with a new variable, 'u', which makes the integral easier to solve. The video script discusses the process of choosing 'u' and how to apply u-substitution to prepare for integration, which is a key strategy for solving more complex integrals.
💡antiderivative
An antiderivative is a function whose derivative is equal to the original function. In calculus, finding the antiderivative is the process of integration. The script refers to finding the antiderivative as part of the integration process, which is essential for solving problems that involve finding areas, volumes, or other quantities that require accumulation.
💡exponents
Exponents, also referred to as 'powers' in the script, are a mathematical concept that indicates how many times a number (the base) is multiplied by itself. Exponents are used extensively in algebra and calculus to express and manipulate mathematical relationships. In the video, exponents are part of the expressions that are being integrated or simplified.
💡fractions
Fractions represent a part of a whole and are typically expressed as the ratio of two integers, with a numerator (the top number) and a denominator (the bottom number). In the video, fractions are discussed in the context of simplifying expressions and preparing them for integration. Fractions are a common component of integrals and are often simplified to make integration easier.
💡derivative
The derivative is a fundamental concept in calculus that represents the rate of change of a function with respect to its variable. It is the antonym of an integral and is used to find slopes of tangent lines, maximize or minimize values, and analyze changes in functions. Although not explicitly mentioned in the script, the concept of derivatives is closely related to integration and is implied in the discussion of calculus.
Highlights

Introduction to handling expressions with powers and radicals, emphasizing their similarities.

Discussion on when to push the radical inside the integral.

Strategy for substituting 'u' in integrals, specifically when the base of the radical is involved.

Mention of the common scenario where replacing 'X' with 'u' does not simplify the expression.

Explanation of the process to simplify the integral by either breaking the fraction or pushing the radical up.

Preference for splitting the fraction as a method of simplification.

Clarification on the meaning of 'integral' in the context of mathematical expressions.

Technique for integrating expressions involving 'u' by pushing the radical up and simplifying.

Rule for integrating expressions of the form 'e^u du'.

Method to simplify 'u' to 'u^(1/2)' before integrating.

Caution to ensure the final answer is simplified, particularly flipping fractions for clarity.

Procedure to reintegrate 'X' into the expression after substitution with 'u'.

Emphasis on the importance of practicing complex scenarios for a deeper understanding.

Transition to a new topic or problem, indicated by moving from 'C' to 'D'.

Highlight on the flexibility of 'u' in different applications and scenarios.

Importance of understanding when not to substitute 'u' to avoid unnecessary complexity.

Final simplification of the integral to '2/3 * (X - 4) + 8' after reintroducing 'X'.

Transcripts

Browse More Related Video

Find The Indefinite Integral By Making A Change Of Variables

Integration Of Exponential Functions [ Substitution Method ]

U Substitution!

Trig Substitution... How? (NancyPi)

Integration Using u-Substitution

Derivative By First Principle Method | Derivative Formula Trick

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsIntegralsRadicalsSubstitutionProblem-SolvingEducationalLearningAlgebraCalculusSimplificationWebinar