Integration Of Exponential Functions [ Substitution Method ]
TLDRThe video script discusses a complex mathematical problem involving integration by substitution. The presenter guides viewers through the process of solving an integral where the variable 'x' is replaced with a new variable 'u', set as 'x - 7'. The key steps include differentiating 'u' to find 'du', substituting back 'x' from 'u', and simplifying the integral expression. The presenter emphasizes the need to break down the fraction and treat each term separately, applying exponent rules to simplify the integrand. The final step involves integrating each term and combining the results to find the antiderivative. The summary concludes with the presenter simplifying the expression to obtain the final answer, which is then translated back in terms of the original variable 'x'. The explanation is detailed, highlighting the importance of each step in the integration process.
Takeaways
- 📚 Start by setting (u = x - 7) and then differentiate to get (du = dx).
- 🔄 Replace all instances of (x) with (u) in the integral, keeping in mind the relationship (x = u + 7).
- 🧐 If the integral involves (x) and it remains after substitution, revert to the original frame of reference.
- 🔢 Isolate (x) by expressing it in terms of (u), which gives (x = u + 7).
- 🔀 Substitute (u + 7) back into the integral to continue the process.
- 📉 The integral simplifies to (\frac{u + 7}{\sqrt{u}} du), which requires further simplification.
- 📈 Break down the fraction into separate terms, resulting in two integrals, one for (u/\sqrt{u}) and another for (7/\sqrt{u}).
- ✅ Simplify (u/\sqrt{u}) to (u^{1/2}) and (7/\sqrt{u}) to (7u^{-1/2}).
- 🔁 Push the exponents up from the denominator to the numerator, resulting in (u^{1/2}) becoming (u^{1/2}) and (7u^{-1/2}) becoming (7u^{-1/2}).
- 📝 Integrate each term separately, noting that the exponents dictate the integration process.
- 🔑 The final integral to solve is (u^{1/2}) and (7u^{-1/2}), which after integration will yield the final answer.
- 🔙 Replace (u) back with (x - 7) to get the final answer in terms of the original variable.
Q & A
What is the first step in the process described in the transcript?
-The first step is to set u equals x minus seven and then derive it to get u equals x.
What does the term 'd u' represent in the context of the script?
-In the context of the script, 'd u' represents the differential element in calculus, used when differentiating with respect to u.
Why do we need to replace 'n' with 'u' in the integral?
-Replacing 'n' with 'u' is a step in the substitution method in integration, which simplifies the integral by changing the variable to make it easier to solve.
What does the term 'u plus seven' represent in the integral?
-The term 'u plus seven' is used to isolate x in terms of u, which is then used to replace x back into the integral after simplification.
How does the process of integrating with respect to u simplify the original integral?
-By substituting x with u in the integral, the process simplifies the original integral into a form that is easier to integrate, often by reducing it to standard forms solvable by basic integration techniques.
What is the significance of breaking the fraction into two parts during the integration process?
-Breaking the fraction into two parts allows for easier integration, as it isolates terms that can be integrated separately, simplifying the overall integration process.
Why is it necessary to push the term '7 over u power half' up in the numerator during the simplification process?
-Pushing the term up to the numerator is a step in the process of rationalizing the denominator, which helps to simplify the expression and prepare it for integration.
What is the final result of the integration process described in the transcript?
-The final result of the integration process is two-thirds of (x minus seven) to the power of one and a half.
How does the exponent change when you add 'one half' to 'minus half' in the expression?
-When you add 'one half' to 'minus half', the result is simply 'half', as the two halves cancel each other out.
What is the rule for changing the sign of the exponent when moving a term from the denominator to the numerator?
-When moving a term from the denominator to the numerator, the sign of the exponent changes from negative to positive or vice versa.
Why is it important to replace 'u' back with 'x minus seven' at the end of the process?
-Replacing 'u' back with 'x minus seven' is important to revert the substitution and express the final answer in terms of the original variable, which is 'x'.
What does the term 'new' represent in the context of the script?
-In the context of the script, 'new' seems to be a mispronunciation or typo for 'u', referring to the substituted variable in the integral.
Outlines
📚 Derivative Simplification with u-Substitution
This paragraph explains the process of simplifying derivatives using the u-substitution method. It begins with the substitution (u = x - 7) and proceeds to demonstrate how to replace 'x' with 'u' in the integral. The explanation details the steps to isolate 'x' and substitute it back to get (x = u + 7). The paragraph then guides through the integration process, emphasizing the need to simplify the expression further before integrating. It concludes with the final integration result, showing the exponent manipulation and the final answer in terms of 'x'.
Mindmap
Keywords
💡Derive
💡Integral
💡Substitution
💡Simplify
💡
💡Exponent
💡Fraction
💡Integration
💡U-Substitution
💡Power
💡Denominator
💡Numerator
Highlights
Deriving u = x - 7 results in u = x
Replacing all instances of x with u in the integral
Isolating x to find x = u + 7
Substituting x back into the integral as u + 7
Simplifying the integral to ∫(u + 7)/√u du
Breaking the fraction into two separate integrals
Simplifying u/√u to u^(1/2)
Simplifying 7/√u to 7u^(-1/2)
Integrating u^(1/2) to get (2/3)u^(3/2)
Integrating 7u^(-1/2) to get (14/3)u^(1/2)
Combining the results to get the final answer of 2/3√(x - 7)
The process involves isolating x, substituting, simplifying, and integrating
The integral involves a challenging scenario where the variable x remains in the expression
The key is to treat the integral in a step-by-step manner, breaking it down into simpler parts
The process requires simplifying the expression and applying integration rules carefully
The final answer is obtained by substituting the original variable x back into the simplified expression
The method demonstrates a thorough approach to solving complex integrals involving substitution and simplification
The step-by-step process is explained clearly, making it easier to understand the solution method
The transcript provides a valuable resource for learning how to approach and solve challenging integrals
Transcripts
Browse More Related Video

[LIVE] zoom Math Calculus For Business | Integrals by substitution #byparts #partialfractionmethod
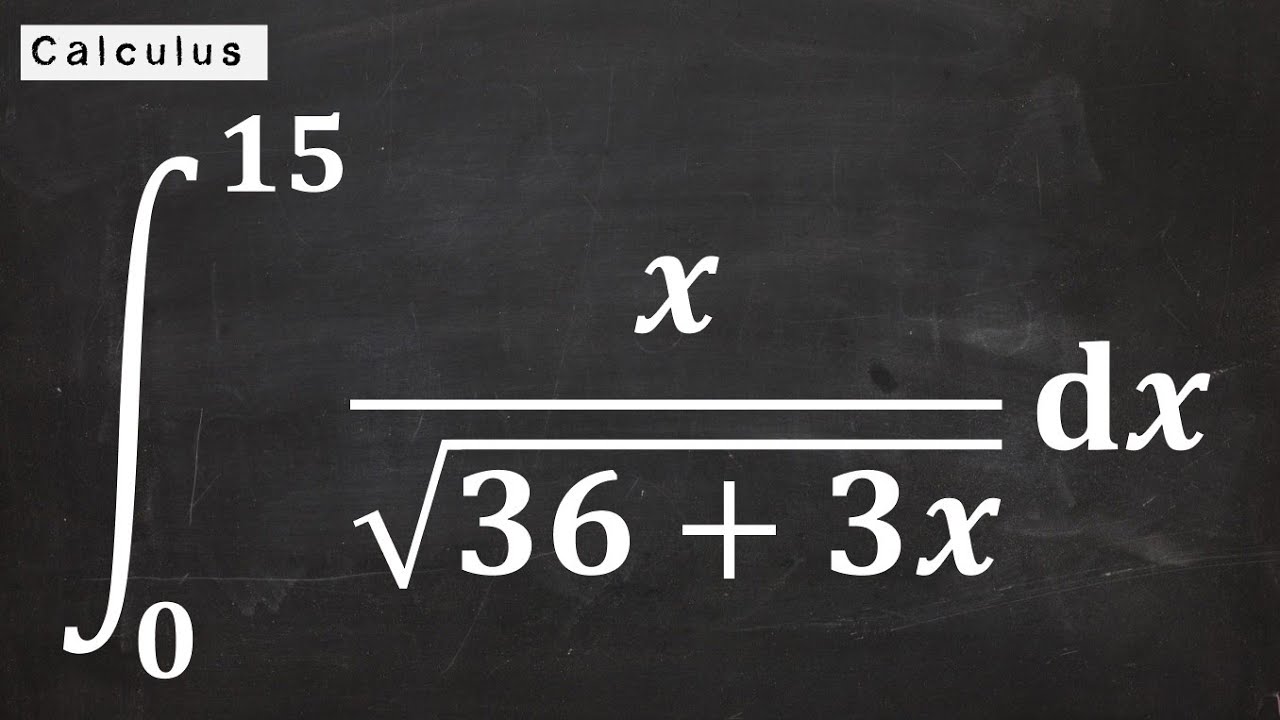
Definite Integral With U-Substitution

Back Substitution - When a u-sub doesn't match cleanly!

U Substitution!

_-substitution intro | AP Calculus AB | Khan Academy

Indefinite Integral of Exponential Functions | Calculus
5.0 / 5 (0 votes)
Thanks for rating: