Trig Substitution... How? (NancyPi)

NancyPi

16 Oct 201826:58

EducationalLearning

32 Likes 10 Comments

TLDRThe video script is an educational guide on trigonometric substitution, a technique used in calculus to simplify the integration of certain expressions involving radicals. The presenter, Nancy, explains that trig substitution is particularly useful when dealing with integrals that have a radical that can't be easily addressed with other methods. She outlines the three main scenarios for trig substitution: sine substitution for expressions of the form (a^2 - x^2), secant substitution for (x^2 - a^2), and tangent substitution for (a^2 + x^2). The script provides a step-by-step approach to each type of substitution, emphasizing the use of Pythagorean identities to eliminate radicals and transform the integral into a more manageable form. Nancy also addresses more complex cases, such as when there's a coefficient on the x^2 term or a radical in the numerator, and provides strategies for converting back to terms of x after substitution. The summary aims to demystify the process, offering students a clear starting point for tackling these challenging integrals.

Takeaways

📚 Trigonometric substitution is a technique used to integrate expressions containing radicals that don't simplify with basic integration methods.
🔍 If the radical contains a term like a^2 - x^2, it suggests using sine substitution. If it's x^2 - a^2, use secant substitution, and for a^2 + x^2, use tangent substitution.
🤔 Before jumping into trigonometric substitution, check if simpler methods like u-substitution, inverse trigonometric integration rules, or other standard integration techniques apply.
🧮 When performing sine substitution, you might use identities like 1 - sin^2 theta = cos^2 theta to simplify expressions.
📐 Pythagorean identity is crucial in trigonometric substitution, helping to eliminate radicals and simplify integrals.
📈 After substitution, you often need to use integration by parts, table of integrals, or other integration techniques to solve the resulting integrals.
🌟 Memorizing common outcomes of trigonometric substitution and their corresponding integral rules can be very helpful in solving problems efficiently.
🔃 To convert the integral result back to terms of x, use the original substitution and any relevant trigonometric identities, such as double-angle identities.
🤓 Trigonometric substitution is not always the most straightforward method, but it's a powerful tool for certain integrals that don't fit more common patterns.
📉 Even when an integral doesn't look like a typical trig substitution form, with some algebraic manipulation, you can often transform it into a form that allows for trig substitution.
💡 Always double-check your work when using trig substitution due to the numerous steps and opportunities for errors, but don't get discouraged if the initial attempt isn't perfect.

Q & A

What is trigonometric substitution used for in calculus?
-Trigonometric substitution is used to eliminate radicals from an integral, making it easier to integrate.
What are the three general cases for trigonometric substitution?
-The three general cases are: 1) a number - x^2 under the radical for sine substitution, 2) a number + x^2 for tangent substitution, and 3) x^2 - a number for secant substitution.
Why might you choose to use trigonometric substitution instead of u-substitution?
-You might choose trigonometric substitution when u-substitution is not applicable, such as when the integral contains a radical that cannot be simplified using standard u-substitution methods.
What is the Pythagorean identity used for in the context of trigonometric substitution?
-The Pythagorean identity is used to simplify expressions involving trigonometric functions, particularly when transforming expressions involving sine and cosine into a form that is integrable.
How do you determine the value of 'a' in the substitution x = a sine theta for a sine substitution?
-The value of 'a' is determined by rewriting the expression under the radical as a^2 - x^2 and comparing it to the sine substitution formula. The value of 'a' is the square root of the constant term in the radical.
What is the half-angle identity used for in trigonometric substitution?
-The half-angle identity is used to simplify expressions involving powers of trigonometric functions, making them easier to integrate after substitution.
How do you convert an integral back from theta to x after performing trigonometric substitution?
-You use the original substitution used to introduce theta, along with any derived relationships between trigonometric functions of theta and x, to back-substitute and express the integral in terms of x.
What is the purpose of the absolute value in the expression for the radical after trigonometric substitution?
-The absolute value ensures that the result is always positive, which is necessary when dealing with indefinite integrals where the sign of the integrand is not specified.
Why is it necessary to check for other integration techniques before resorting to trigonometric substitution?
-It is important to check for other techniques like u-substitution, inverse trigonometric integration rules, or partial fraction decomposition because they may provide a simpler or more direct method to integrate the given expression.
What is the role of trigonometric integral rules in solving complex integrals after substitution?
-Trigonometric integral rules help in integrating expressions involving powers of trigonometric functions by strategically saving one trigonometric function and converting the rest using Pythagorean identities.
How can you handle an integral with a coefficient on the x^2 term under the radical using trigonometric substitution?
-You can handle it by rewriting the expression as u^2 + a^2, where u represents the coefficient on x^2, and then using an appropriate trigonometric substitution based on the form of the expression.

Outlines

00:00

📚 Introduction to Trigonometric Substitution

Nancy introduces the concept of trigonometric substitution for integration, emphasizing its complexity and the importance of jumping right into the process. She outlines the telltale signs of when to use trig substitution, which is typically when a radical expression is present and other integration methods have failed. Nancy explains the three main types of trig substitution: sine for a number minus x^2 under the radical, secant for the reverse, and tangent for a number plus x^2. She also discusses why certain other substitution methods, like u-substitution or inverse trigonometric integration rules, are not applicable in this context.

05:04

🔁 Sine Substitution and Pythagorean Identity

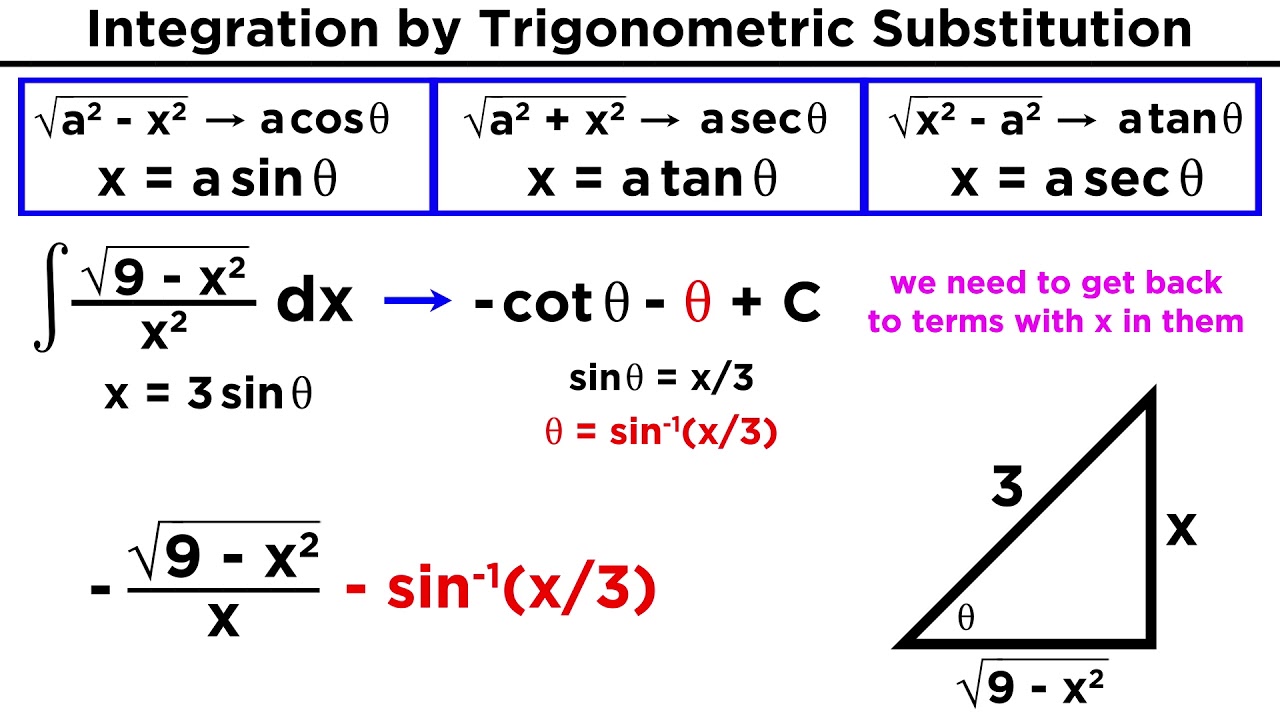
The paragraph delves into the specifics of sine substitution, illustrating how to identify when to use it based on the structure of the radical expression. Nancy demonstrates the substitution process by setting x = 6 sine theta, given the radical's form. She emphasizes the role of the Pythagorean identity in simplifying the radical and transforming it into a form that can be integrated. The summary includes the steps to rewrite the integral in terms of theta, including replacing dx and x^2 with their theta equivalents, and the importance of handling absolute value expressions in indefinite integrals.

10:07

🎓 Advanced Trigonometric Integration Techniques

Nancy provides a comprehensive guide on how to proceed after performing trigonometric substitution. She advises leveraging knowledge of trigonometric function integration, algebraic tricks, and identities to solve the resulting integral. Common outcomes of trig substitution are presented, along with the corresponding integral rules from the table of integrals that may be required. The paragraph also covers the use of half-angle identities and the potential need for trig integral rules when dealing with products and quotients of trig functions with powers.

15:07

🔄 Converting Back to x-Terms and Double-Angle Identity

This section focuses on the process of converting the integral solution back to terms of x after performing trig substitution. It explains the use of the double-angle identity for simplifying sine of 2 theta expressions and converting them into terms of x using the original substitution x = 6 sine theta. The paragraph also covers how to obtain expressions for other trigonometric functions, like cosine theta, using right triangle trigonometry and the Pythagorean theorem.

20:07

🤔 Handling Coefficients and Numerator Radicals

Nancy addresses more complex scenarios where the integral involves coefficients on the x^2 term or a radical in the numerator. She explains how to approach these using trig substitution, specifically focusing on tangent substitution when there's a coefficient on x^2. The paragraph outlines the process of rewriting the expression to fit the substitution criteria, substituting, and simplifying to an integrable form. It also touches on the potential need for trig integral rules when powers of secants and tangents are involved.

25:11

🧩 Special Cases and Unfamiliar Forms

The final paragraph discusses special cases and forms that might not immediately appear suitable for trig substitution but can still be tackled using this method. Nancy covers instances where the integral has no radical, but the form suggests trig substitution could be applied. She also talks about the use of trig substitution with rational powers and how to rewrite expressions to make them more amenable to this technique. The summary reassures learners that even if the integral doesn't fit the standard form, with a bit of algebraic manipulation, trig substitution can still be a viable approach.

Mindmap

Keywords

💡Trigonometric Substitution

Trigonometric substitution is a mathematical technique used to simplify the process of integrating expressions involving radicals, particularly those that are not easily integrable by standard methods. In the video, it is the central theme, where the presenter, Nancy, guides viewers through the process of using trigonometric substitution to integrate complex expressions. It is exemplified through various cases such as sine, secant, and tangent substitutions.

💡Radical

A radical, specifically in the context of integration, refers to the square root or other root of an expression. The video discusses how to eliminate radicals through trigonometric substitution to simplify integrals. For instance, when an expression has a radical in the form of a^2 - x^2, a sine substitution is suggested.

💡Pythagorean Identity

The Pythagorean identity is a fundamental relationship in trigonometry stating that 1 - sin^2(θ) = cos^2(θ). In the video, this identity is crucial for simplifying expressions after trigonometric substitution. It is used to transform expressions involving sine and cosine into more manageable forms for integration.

💡Sine Substitution

Sine substitution is a specific type of trigonometric substitution used when the expression under the radical is of the form a^2 - x^2. In the video, it is one of the first methods introduced, with the substitution x = a * sin(θ) used to eliminate the radical and simplify the integral.

💡Secant Substitution

Secant substitution is used when the expression under the radical is of the form x^2 - a^2, which is the reverse of the sine substitution case. The video explains that this method involves substituting x with a * sec(θ) to facilitate integration and is an example of how to handle expressions with a different arrangement of terms under the radical.

💡Tangent Substitution

Tangent substitution applies to integrals with a radical in the form of x^2 + a^2. The video demonstrates that by substituting x with a * tan(θ), the radical can be eliminated, allowing for easier integration. It is another key strategy in the trigonometric substitution toolkit.

💡Half-Angle Identity

A half-angle identity is a trigonometric identity that relates the sine or cosine of half an angle to the sine or cosine of the full angle. In the video, the presenter uses the half-angle identity to simplify expressions involving sine^2(θ) by transforming them into a form that can be more easily integrated.

💡Double-Angle Identity

The double-angle identity is a trigonometric formula that expresses the sine or cosine of twice an angle in terms of the sine and cosine of the original angle. In the video, it is used to convert expressions like sin(2θ) into a form involving sin(θ) and cos(θ), which is helpful for back-substitution into the original integral.

💡Integration by Parts

Integration by parts is a method for integrating a product of two functions. Although not the primary focus of the video, it is mentioned as an alternative technique that may be necessary if specific trigonometric integral rules do not apply. It highlights the variety of methods available for integration and the need to choose the appropriate one based on the integral's form.

💡Trig Integral Rules

Trig integral rules are specific formulas used to integrate expressions involving trigonometric functions with powers. In the video, these rules are suggested for simplifying integrals that result from trigonometric substitution. They are a key part of the strategy for integrating complex trigonometric expressions.

💡Back-Substitution

Back-substitution is the process of replacing the trigonometric variables used in the substitution process back into their original algebraic form to express the final answer in terms of the original variable, which in the video is x. It is a crucial step in completing the integration using trigonometric substitution, ensuring the final answer is in the desired form.

Highlights

Trigonometric substitution is a technique used to integrate expressions containing radicals, especially when other methods like u-substitution don't work.

The choice of trigonometric substitution depends on the form of the radical: sine substitution for a^2 - x^2, secant for x^2 - a^2, and tangent for a^2 + x^2.

Before trigonometric substitution, check if the integral can be solved using u-substitution, inverse trigonometric integration rules, or other standard techniques.

Sine substitution involves rewriting the radical as a^2 - x^2 and using the identity 1 - sin^2(θ) = cos^2(θ) to simplify the integral.

In trigonometric substitution, the Pythagorean identity is crucial for simplifying expressions and eliminating radicals.

When performing trigonometric substitution, assume that trigonometric functions like cosine are positive when dealing with indefinite integrals.

After substitution, the integral should be expressed entirely in terms of the new variable, such as θ, to facilitate integration.

Common outcomes of trigonometric substitution can be integrated using standard integral rules for trigonometric functions.

Half-angle identities and power-reducing identities are often necessary to simplify the integral after trigonometric substitution.

Reverting the integral result back to the original variable, such as x, requires using the substitution and double-angle identities where applicable.

Tangent substitution is used when the radical has the form a^2 + x^2, and it involves expressing 5x = 2tan(θ) and simplifying the integral.

Trigonometric integral rules can be applied when the integral contains powers of secants and tangents or sines and cosines.

Secant substitution is applicable for forms like x^2 - a^2 and involves expressions like x = a sec(θ).

Trigonometric substitution can handle integrals with rational powers by rewriting them as roots raised to a power.

Even when an integral does not explicitly contain a radical, trigonometric substitution can still be applied if the form suggests one of the known patterns.

Completing the square can transform certain integrals into a form that allows for the application of trigonometric substitution.

Trigonometric substitution is a versatile technique for integrating complex expressions, although it can be quite involved and require multiple steps.

It's important to double-check work when using trigonometric substitution due to the many opportunities for errors in the process.

Transcripts

Browse More Related Video

Lec 28 | MIT 18.01 Single Variable Calculus, Fall 2007

Integration Using u-Substitution

Integration By Trigonometric Substitution

How to Integrate Using U-Substitution (NancyPi)

Lesson 16- Integration By Trig Substitution (Calculus 1 Tutor)

Calculus 2 - Basic Integration

Related Tags

Trig Substitution Integral Calculus Math Tutorial Trigonometry Substitution Methods Sine Substitution Secant Substitution Tangent Substitution Pythagorean Identity Trig Integrals Math Education