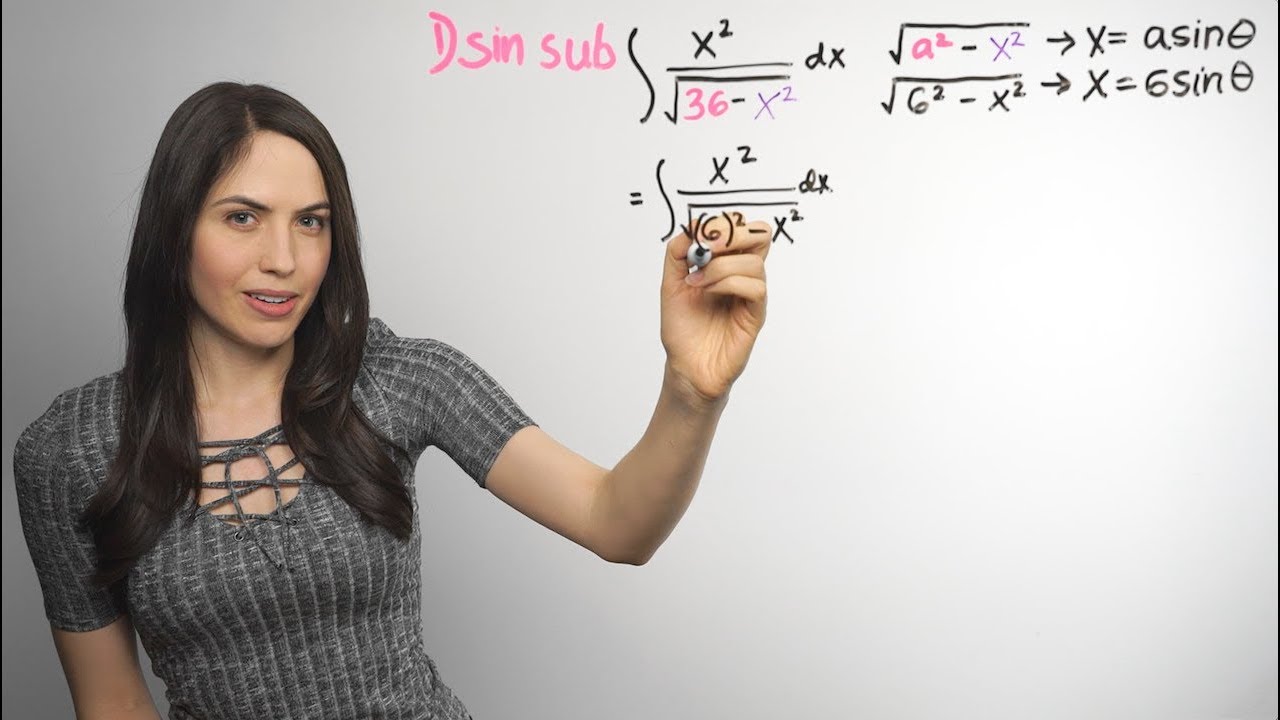Integration Using u-Substitution
TLDRThis video tutorial delves into the method of integration using U-substitution, a technique for evaluating complex integrals that don't have straightforward formulas. The instructor demonstrates how to apply U-substitution to several integrals involving algebraic functions and radicals, transforming them into more manageable forms. By using the power rule for integration and carefully handling differentials, the video guides viewers through the process of finding the antiderivative of expressions like (3x - 4)^5, (x^3 + 2)^2, and others. The step-by-step explanations aim to clarify the integration process and empower viewers with the knowledge to tackle challenging integrals effectively.
Takeaways
- 📚 The video teaches integration using U-substitution, a method for evaluating complex integrals.
- 🔍 U-substitution is preferred for integrals involving algebraic functions that don't have an existing formula.
- 🌟 The power rule for integration is fundamental when applying U-substitution.
- 📝 The first example demonstrates integrating (3x - 4)^5 using U = 3x - 4, resulting in a simplified expression.
- 🧠 The process involves finding a suitable U, differentiating both sides, and substituting in the integral.
- 📊 For the second problem, the cube root of x plus 2 is squared, and U-substitution is used to find the integral.
- 🛠️ The third example shows integrating a function with a square root by first converting it to a fractional exponent.
- 📐 The fourth example involves a more complex integral with a radical in the denominator, which is simplified using U-substitution.
- 🔗 The fifth example demonstrates integrating a function with a square root in the numerator and a complex denominator.
- 📝 The sixth example is about integrating a function with a square root in the denominator, which is transformed using U-substitution.
- 🎓 The video concludes with a summary of the integrals solved and encourages viewers to apply the learned concepts.
Q & A
What is the main topic of the video?
-The main topic of the video is integration using U-substitution, a technique for evaluating integrals that are difficult to solve using standard formulas.
When is U-substitution typically used?
-U-substitution is typically used when dealing with integrals involving algebraic functions that cannot be easily evaluated using existing formulas.
What is the first integral example provided in the video?
-The first integral example provided is the integral of (3x - 4)^5 dx.
How does the video demonstrate the U-substitution process for the first example?
-The video demonstrates the U-substitution process by letting U be equal to (3x - 4), finding its derivative (dU), and then substituting U and dU back into the integral to simplify and evaluate it.
What is the power rule for integration mentioned in the video?
-The power rule for integration states that the integral of U^n du is equal to (U^(n+1))/(n+1) + C, where n is not equal to -1.
What is the final result of the first integral example after applying U-substitution?
-The final result of the first integral example is (1/18)(3x - 4)^6 + C.
How does the video handle the second integral example involving a cube root?
-The video handles the second example by first transforming the cube root into a fractional exponent, then applying U-substitution with U equal to (x + 2), and finally evaluating the integral using the power rule.
What is the significance of the negative exponent in the fourth integral example?
-The negative exponent in the fourth integral example indicates the need to apply the power rule with a negative exponent, which is handled by converting the negative exponent to a positive one and then simplifying the result.
How does the video address the extra coefficient in the third integral example?
-The video addresses the extra coefficient in the third integral example by dividing both sides of the equation by the coefficient (negative four) to eliminate it and then proceeding with the U-substitution and evaluation.
What is the final answer for the fifth integral example involving the square root of x?
-The final answer for the fifth integral example is (5/4) times (1 + sqrt(x))^(8/5) + C.
What is the key takeaway from the video?
-The key takeaway from the video is the step-by-step process of using U-substitution to evaluate complex integrals, including the transformation of expressions, application of the power rule, and the final substitution back into the original variable.
Outlines
📚 Introduction to U-Substitution in Integration
The opening segment introduces the concept of U-Substitution as a method to evaluate integrals that are difficult to solve with basic formulas. The narrator emphasizes its application to algebraic functions and the use of the power rule, recommending viewers to watch a previous video on basic integration for foundational knowledge. The technique involves selecting a part of the integral to represent as 'U', making the integral simpler to solve. The first example discussed is the integral of (3x - 4)^5, demonstrating how to choose 'U', differentiate it, and apply the substitution to solve the integral effectively.
🔢 Solving Diverse Integrals Using U-Substitution
This part covers the application of U-Substitution in solving various integrals. The narrator begins with an integral involving a cube root and squared terms, showing the transformation to fractional exponents and the subsequent substitution process. Following this, an integral featuring a cube and a square root is tackled, highlighting the transformation of square roots to fractional exponents and the strategic choice of 'U'. The narrator methodically explains each step of the substitution, differentiation, and simplification process, culminating in the final solutions for these complex integrals.
🧮 Advanced Techniques and Examples of U-Substitution
The third section delves into more complicated examples to illustrate the versatility of U-Substitution. It starts with an integral involving division by a power function, guiding viewers through choosing 'U', differentiating it, and simplifying the expression to solve the integral. Another example demonstrates dealing with an integral of a rational function over a square root, showcasing how to manipulate expressions and apply U-Substitution effectively. The narrator explains each step thoroughly, from substitution to simplification, ensuring viewers understand how to apply these techniques to different types of integrals.
🎓 Concluding Examples and Wrap-Up on U-Substitution
The final segment presents the last examples of integrating using U-Substitution, focusing on integrals that involve square roots and rational functions. The narrator walks through the process of selecting 'U', differentiating, and substituting back into the integral for each example. Detailed explanations are provided on how to simplify and evaluate the integrals, concluding with the transformation back to the original variable. The video wraps up by reinforcing the utility of U-Substitution in solving complex integrals and encourages viewers to practice what they've learned.
Mindmap
Keywords
💡Integration
💡U-Substitution
💡Power Rule
💡Derivative
💡Differential
💡Algebraic Functions
💡Binomial
💡Antiderivative
💡Coefficient
💡Constant
Highlights
Introduction to integration using U-substitution
U-substitution is used for integrals that cannot be easily evaluated using existing formulas
Focus on integrals involving algebraic functions and the power formula for integration
Example 1: Integral of (3x - 4)^5
U-substitution applied by letting U equal to (3x - 4)
Derivative calculation for U-substitution
Transforming the integral to terms of U and solving using power rule
Example 2: Integral of (cube root of x + 2)^2
Transforming the radical to fractional exponent and applying U-substitution
Example 3: Integral of x * (cube root of (1 - x^4))
Applying U-substitution with the expression inside the radical
Dividing by a coefficient to simplify the integral
Example 4: Integral of (x^5)/(x^6 - 1)^5
Solving the integral by making the denominator a negative exponent
Example 5: Integral of (1 + sqrt(x))^5/sqrt(x)
Multiplying both sides by a coefficient to simplify the derivative
Example 6: Integral of (2x + 1)/(sqrt(x^2 + x + 1))
Derivative of the expression under the square root and applying U-substitution
Final answer for the integral using U-substitution and transforming back to x
Conclusion and summary of integration using U-substitution
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: