BusCalc 13.2 Integration by Substitution
TLDRThe video script is an in-depth tutorial on antiderivatives and the method of integration by substitution in calculus. It begins with an explanation of the power rule for antiderivatives, illustrating how to find antiderivatives of functions like x^3 and √x. The instructor emphasizes the importance of adding a constant 'C' when finding antiderivatives and suggests verifying answers by differentiating the result to check if it matches the original function. The script then delves into the integration by substitution method, a technique for finding antiderivatives of more complex functions. The process involves choosing a suitable expression for 'u', finding du/dx, solving for dx, substituting 'u' and dx in the original integral, and simplifying. Several examples are provided to demonstrate the method, including integrals involving exponential and logarithmic functions. The instructor also discusses common pitfalls, such as choosing the wrong 'u' substitution, and the importance of practice in mastering the technique. The tutorial concludes with a reminder to be careful with each step, as even small errors can lead to incorrect results, and encourages students to practice to improve their skills.
Takeaways
- 📚 The process of finding anti-derivatives often involves applying the power rule, which includes adding 1 to the exponent and dividing by the new exponent, plus an additional constant (C).
- 🔍 When dealing with square roots, it's important to recognize that the square root of x is equivalent to x to the power of 1/2, which simplifies the process of finding anti-derivatives.
- ❌ For certain functions like x to the power of -1, direct application of the power rule is not possible due to division by zero; instead, use the natural logarithm function.
- 🔑 The additivity property of anti-derivatives allows us to treat each term in a sum separately when finding the overall anti-derivative.
- 🧐 To check the work after finding an anti-derivative, one can take the derivative of the result and verify it matches the original integrand.
- 📉 For functions that do not have straightforward anti-derivatives, methods like integration by substitution can be used, which involves choosing a suitable expression for 'u', finding du/dx, and substituting these into the integral.
- 🔄 The reverse substitution step in integration by substitution is crucial to express the final answer in terms of the original variable, often x.
- 🚫 Choosing the incorrect 'u' in integration by substitution can lead to dead ends, and it's important to recognize when to backtrack and try a different 'u'.
- 🤔 The choice of 'u' in integration by substitution often involves recognizing a pattern or function within the integral that simplifies upon substitution, such as the inner function of a composition.
- 🛠️ Integration by parts and integration by substitution are two advanced methods for finding the anti-derivatives of more complicated functions.
- ⏱️ Practice and patience are key in integration by substitution, as the correct 'u' is not always immediately obvious and may require trial and error.
Q & A
What is the correct process for finding the antiderivative of a function?
-The process involves identifying the function to integrate, applying the power rule which involves adding 1 to the exponent and then dividing by the new exponent, and including the constant of integration 'c'.
How do you find the antiderivative of x^(-1)?
-Since you can't divide by zero, x^(-1) is undefined using the power rule directly. Instead, recognize that x^(-1) is the same as 1/x, and its antiderivative is the natural logarithm of the absolute value of x plus a constant c.
What is the antiderivative of e^(2x)?
-Using the property that the antiderivative of an exponential function e^(ax) is (1/a)e^(ax) + c, the antiderivative of e^(2x) is (1/2)e^(2x) + c.
How can you check your answer after finding an antiderivative?
-You can check your answer by differentiating the antiderivative and verifying that you obtain the original integrand.
What is the main idea behind integration by substitution?
-Integration by substitution is a method used when the integral is a combination of functions that are difficult to integrate directly. You choose a suitable expression (u), find du/dx, rearrange to solve for dx, substitute u into the integral, simplify, and then take the antiderivative.
What should you do if the antiderivative you found still contains the original variable (x) after substitution?
-If the antiderivative still contains x, it means the choice of u was incorrect. You should erase your work and try a different substitution.
How do you choose the correct expression for 'u' in integration by substitution?
-A common strategy is to choose an expression that is part of the integral and for which you know the antiderivative. It often involves recognizing a function composition or a pattern that simplifies upon substitution.
What is the antiderivative of 3x * e^(x^2) with respect to x?
-You would choose x^2 as u, then find du/dx = 2x, rearrange to dx = (1/2x) du, substitute into the integral, and simplify to find the antiderivative.
What is the antiderivative of (2t) / (t + 3)^5 with respect to t?
-You would choose t + 3 as u, find du/dt = 1, and rearrange to dt = du. Then substitute into the integral and simplify to find the antiderivative.
Why is it important to have only 'u' terms in the antiderivative after substitution?
-Having only 'u' terms ensures that you can apply the antiderivative power rule or other known antiderivative formulas to find the integral. If 'x' terms remain, it indicates an incorrect choice of substitution.
How does the process of integration by substitution simplify the integral of (2t - 3t^2) * (t^2 - t^3)^7 dt?
-By choosing u = t^2 - t^3, the integral simplifies because du/dt matches the first part of the integrand, allowing for a straightforward substitution and application of the antiderivative power rule.
Outlines
📚 Anti-Derivative Rules and Power Rule Application
The paragraph explains the process of finding anti-derivatives using basic rules, such as adding one to the exponent and dividing by the new exponent, including the importance of including the constant 'c'. It also touches on the concept of the power rule and how it applies to various functions, including x cubed, square root of x, and x to the power of negative one. The paragraph emphasizes the method of checking answers by differentiating the antiderivative to see if it matches the original function.
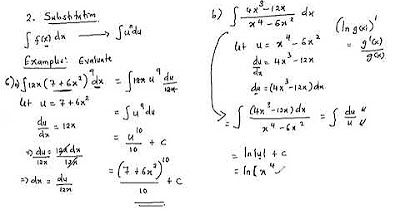
🧐 Integration by Substitution Method Overview
This section introduces the integration by substitution method, highlighting that there is no direct product, quotient, or chain rule for anti-derivatives. It outlines the steps for integration by substitution, which includes choosing a suitable expression (lowercase u), finding its derivative, solving for dx, substituting u into the integral, taking the anti-derivative, and finally reversing the substitution to express the answer in terms of x.
🔍 Substitution Method Example with Detailed Steps
The paragraph walks through an example of the substitution method, starting with choosing u=1-5x and proceeding through the steps of finding du/dx, rearranging to solve for dx, substituting u into the integral, and taking the anti-derivative. It concludes with the reverse substitution and emphasizes the importance of checking the answer by differentiating to ensure it matches the original integrand.
🧠 Choosing the Right u for Substitution Method
This part discusses the importance of selecting the correct u in the substitution method and provides a trial and error approach to finding the right u. It explains that the correct choice of u is often the inner function and that it can be a process of trial and error. The paragraph also provides an example of an incorrect u choice and how to recognize and correct it.
🔑 Correct u Selection and Simplification Process
The paragraph emphasizes the importance of selecting the correct u for the substitution method and demonstrates the simplification process when the right u is chosen. It shows how to substitute, simplify the integral, and take the anti-derivative. It also illustrates the process of reverse substitution and checking the answer by differentiation.
🤔 Dealing with Complex Integrals Using Substitution
This section deals with complex integrals and the use of the substitution method to simplify them. It discusses the process of choosing a suitable u, rearranging to solve for dt, substituting into the integral, and taking the anti-derivative. The paragraph also highlights the potential need for multiple attempts to find the correct u and the importance of checking the final answer.
📉 Anti-Derivative of Functions with Exponentials and Logs
The paragraph focuses on finding anti-derivatives of functions involving exponentials and logarithms. It explains the process of choosing an appropriate u, rearranging to solve for dt, substituting u into the integral, and taking the anti-derivative. It also demonstrates the reverse substitution and the process of checking the answer by differentiating.
🛣️ Simplifying Complex Expressions Using u-Substitution
This section provides an example of simplifying a complex expression using the u-substitution method. It shows how to identify the correct u, rearrange to solve for dt, and substitute into the integral. The paragraph illustrates the simplification process, taking the anti-derivative, and the final step of reversing the substitution to express the answer in terms of the original variable.
🧩 Expanding and Simplifying Polynomial Expressions
The paragraph discusses an alternative approach to solving complex polynomial expressions by expanding and multiplying them out, resulting in a polynomial with multiple terms. However, it highlights that this method, while possible, is time-consuming and prone to errors. It then contrasts this with the u-substitution method, which is shown to be more efficient and less error-prone.
📝 Final Example and Class Closing Remarks
The final paragraph provides a complex example of using the u-substitution method, guiding through the process of choosing u, solving for dt, substituting into the integral, and simplifying. It concludes with an encouragement for students to practice the method and offers help for any roadblocks they may encounter, emphasizing the goal of mastering the u-substitution technique.
Mindmap
Keywords
💡Anti-derivative
💡Power Rule
💡Substitution Method
💡Chain Rule
💡Additivity Property
💡Natural Logarithm
💡Exponential Function
💡Derivative
💡Integration by Parts
💡Product Rule
💡Quotient Rule
Highlights
The process of finding anti-derivatives involves adding one to the exponent and dividing by the new exponent, with the inclusion of a constant 'c'.
For square root of x, the anti-derivative is x to the power of 3/2, which simplifies to multiplying by 2/3.
The anti-derivative of x to the power of -1 is the natural log of the absolute value of x plus a constant 'c'.
The anti-derivative can be found for each term in a polynomial separately due to the additivity property.
To verify an anti-derivative, one can take the derivative of the answer and check if it matches the original integrand.
Integration by substitution is a method to handle more complicated anti-derivatives, involving choosing a suitable expression as 'u'.
The derivative of the chosen 'u' is taken with respect to x, and then solved for dx to facilitate substitution.
The reverse substitution is performed at the end of the integration by substitution process to express the final answer in terms of x.
The anti-derivative of a function composed of a product of two functions does not have a direct product rule, quotient rule, or chain rule.
Choosing the correct 'u' in integration by substitution can be a trial and error process and requires practice to master.
When performing integration by substitution, if the anti-derivative contains x's, the choice of 'u' was incorrect and needs to be re-evaluated.
The anti-derivative of e to the power of u (where u is a function of x) is e to the power of u plus a constant 'c'.
The derivative of the natural log of a function is 1 over the function, which is used in reverse substitution to check answers.
The choice of 'u' can often be the inner function in a composite function, which simplifies the integral when performing substitution.
The process of integration by substitution can be used to simplify and solve complex integrals that do not have obvious anti-derivatives.
The derivative of a constant times a function is the constant times the derivative of the function, which is applied when simplifying integrals.
When the anti-derivative is taken and the result only contains 'u', it is a sign that the correct substitution has been made.
The anti-derivative of a function raised to a power involves increasing the exponent by one and dividing by the new exponent.
The use of the antiderivative additivity rule allows for breaking down complex integrals into the sum or difference of simpler integrals.
Transcripts
Browse More Related Video

U-Substitution 5-sample video

Find The Definite Integral Of x3 Into 3 Plus x Power 4 All Power -2 [Evaluate The Definite Integral]

Definite Integral Calculus Examples, Integration - Basic Introduction, Practice Problems
Integration using substitution method
Definite Integral With U-Substitution
U-Substitution with Definite Integrals
5.0 / 5 (0 votes)
Thanks for rating: