calculating work, pumping water out of a rectangular tank, calculus 2 tutorial

blackpenredpen
25 Apr 201507:36
EducationalLearning
32 Likes 10 Comments

TLDRThe script explains the process of calculating the work required to pump out half of the water from a Korean aquarium measuring 2 meters long, 1 meter wide, and 1 meter deep. It emphasizes the importance of understanding the concept of work as force times distance, and the need to consider the weight of water, its volume, density, and the effect of gravity. The explanation involves visualizing the aquarium, drawing a horizontal slice to represent the top half of the water, and setting up an integral to calculate the work needed to pump out this portion of water, using appropriate units and constants.

Takeaways
  • 📏 The dimensions of the Korean aquarium are 2 meters long, 1 meter wide, and 1 meter deep.
  • 💧 The aquarium is initially filled with water, and the task is to calculate the work needed to pump out half of the water.
  • 🔧 Work in this context is defined as Force Times Distance, where force is the weight of the water.
  • 📐 To find the weight, the formula involves volume times the density of water (1000 kg/m³) and gravity (9.8 m/s²).
  • 📏 The volume of the water is calculated by multiplying the length, width, and a small vertical change (dy).
  • 📚 The script emphasizes the importance of using consistent units, SI units in this case, for calculations.
  • 📈 The process involves integrating the volume of water slices from the bottom to halfway up the aquarium.
  • 📉 The integration is performed from y=0 to y=0.5, representing the top half of the water.
  • 🔄 The script explains the use of a reference frame to determine the distance the water must travel to be pumped out.
  • 📝 The final work calculation results in 20.15 Joules, assuming the reference frame is set with the bottom at y=0.
  • 🔄 An alternative reference frame is suggested, which would yield a different calculation for the work but the same result.
Q & A

  • What are the dimensions of the Korean aquarium mentioned in the script?

    -The Korean aquarium is 2 meters long, 1 meter wide, and 1 meter deep.

  • What is the purpose of calculating work in the context of the script?

    -The purpose is to determine the amount of work needed to pump out half of the water from the aquarium.

  • What is the formula for calculating work in this context?

    -Work is calculated as Force Times Distance, where force is the weight of the water to be pumped.

  • How is the weight of the water determined in the script?

    -The weight is determined by multiplying the volume of the water by its density and then by the acceleration due to gravity (9.8 m/s²).

  • What is the density of water used in the calculations?

    -The density of water used in the calculations is 1000 kilograms per cubic meter.

  • How is the volume of the water in the top half of the aquarium expressed mathematically?

    -The volume of the top half of the water is expressed as 1 (meter) * 2 (meters) * dy, where dy represents a small change in the depth from the top.

  • What is the significance of the variable 'dy' in the script?

    -The variable 'dy' represents a small vertical change in the depth of the water as the top half is being considered for pumping.

  • What is the method used to calculate the total work required to pump out the water?

    -The method used is integration, where the expression for the work for each small slice of water is integrated over the range from 0 to 0.5 meters of depth.

  • What is the SI unit used to express the calculated work?

    -The SI unit used to express the calculated work is the Joule.

  • How does the script suggest setting up the reference frame for the integration?

    -The script suggests setting up the reference frame with the x-axis and y-axis, where y represents the distance from the bottom of the aquarium to the top of the water slice.

  • What is the final result of the integration for pumping out half of the water?

    -The final result of the integration is 2450 Joules, assuming the correct setup and calculation.

Outlines
00:00
📏 Calculating Work to Pump Water from a Rectangular Aquarium

This paragraph discusses the process of calculating the work required to pump out half the water from a rectangular aquarium that is 2 meters long, 1 meter wide, and 1 meter deep. It explains the concept of work as force times distance, and how to determine the force by considering the weight of the water, which is calculated by volume times density (1000 kg/m³ for water) and gravity (9.8 m/s²). The paragraph then describes a method to visualize and calculate the volume of a horizontal water slice using integration, focusing on the top half of the water to find the work needed to pump it out.

05:01
🔢 Detailed Integration Process for Pumping Water

The second paragraph delves into the integration process to calculate the work required to pump out water from the top half of the aquarium. It outlines the steps to set up the integral, considering the volume of a water slice as a function of the vertical distance 'y' from the bottom of the aquarium. The density and gravity constants are applied to find the force, and the distance 'Y' is used to calculate the work for each slice. The integration is performed from the bottom (Y=0) to halfway up the aquarium (Y=0.5), resulting in a work value in joules. The paragraph also discusses an alternative reference frame for calculating the work, yielding the same result, emphasizing the consistency of the physical principles involved.

Mindmap
Keywords
💡Work
In the context of this video, 'work' is a physics term referring to the amount of effort required to move an object against a force, such as gravity. It is calculated as the product of force and the distance over which the force is applied. The video discusses calculating the work needed to pump water out of a container, illustrating this concept by considering the force exerted by the water's weight and the distance it must be lifted.
💡Force
'Force' is a fundamental concept in physics that represents the push or pull upon an object resulting from its interactions. In the video, force is equated to the weight of the water in the aquarium, which is essential for determining the work required to pump the water out.
💡Density
Density is defined as mass per unit volume and is crucial in the script for calculating the weight of the water. The video mentions the density of water as 1000 kilograms per cubic meter, which is used to find the force exerted by the water's weight.
💡Volume
Volume in the video refers to the amount of space occupied by the water in the aquarium. It is a key factor in determining the weight of the water and, subsequently, the work needed to pump it out. The script describes how to calculate the volume of a horizontal slice of water in the aquarium.
💡Aquarium
The 'aquarium' is the central object in the video's scenario. It is described as a rectangular container filled with water, and the script discusses the dimensions of the aquarium, which are necessary for calculating volume and subsequently the work required to remove half of the water.
💡Gravity
In the script, 'gravity' is the force that pulls objects towards the center of the Earth. It is a constant factor in the calculation of work, as it influences the weight of the water. The video uses the acceleration due to gravity (9.8 m/s²) to calculate the force exerted by the water.
💡Integration
Integration is a mathematical process used in the video to calculate the total work required to pump out half of the water in the aquarium. It involves summing up the work done for each thin horizontal slice of water from the bottom to halfway up the aquarium.
💡Slice
In the context of the video, a 'slice' refers to a thin horizontal section of the water within the aquarium. The script describes calculating the volume of each slice and how the work varies as you move up from the bottom to the halfway point of the aquarium.
💡Distance
'Distance' in the video is the vertical height that the water must be pumped, which is a factor in calculating the work. The script discusses how the distance varies for each slice of water and how it affects the total work required.
💡SI Units
SI Units, or International System of Units, is the modern form of the metric system used in the video for measurements. The script mentions using joules as the unit for work, which is part of the SI system, emphasizing the importance of consistent units in scientific calculations.
💡Reference Frame
A 'reference frame' is a set of criteria or a system used to measure and observe motion or other physical properties. In the video, the reference frame is used to define the starting and ending points for calculating the work done on each slice of water as it is pumped out.
Highlights

Calculating the work required to pump out half of the water from a rectangular aquarium using the formula for work (Force x Distance).

Determining the force needed by calculating the weight of the water, which is the product of volume, density, and gravity.

Using the dimensions of the aquarium (2m length, 1m width, 1m depth) to find the volume of water.

Focusing on the top half of the water for the calculation by considering a horizontal slice through the middle of the aquarium.

Deriving the volume expression for the water slice as length (2m) times width (1m) times the small vertical change dy.

Multiplying the volume expression by the density of water (1000 kg/m³) and gravity (9.8 m/s²) to find the force.

Identifying the distance the water needs to be pumped as the vertical distance Y from the slice to the top of the aquarium.

Setting up an integral to calculate the work by integrating the force over the distance from the bottom half (Y=0) to the middle (Y=0.5m).

Performing the integration to find the work required to pump out the top half of the water, resulting in 20,150 Joules using SI units.

Alternative reference frame setup by considering the water's widest Y distance above the x-axis for the calculation.

Adjusting the volume expression to account for the Y distance and integrating from the bottom to halfway point for the work calculation.

Using the alternative setup, the integral calculation also results in 20,150 Joules, demonstrating the consistency of the method.

Emphasizing the importance of unit consistency and correct labeling for accurate work calculations.

Highlighting the practical application of the work formula in real-world scenarios like pumping water out of an aquarium.

Explaining the process in a step-by-step manner to ensure clarity and ease of understanding.

Using visual aids like drawings to illustrate the concept of slicing the water and calculating the volume of each slice.

Mentioning the possibility of using different reference points for the calculation without affecting the final result.

Transcripts

Browse More Related Video

Calculate Work to Pump Water Out of Rectangular Tank

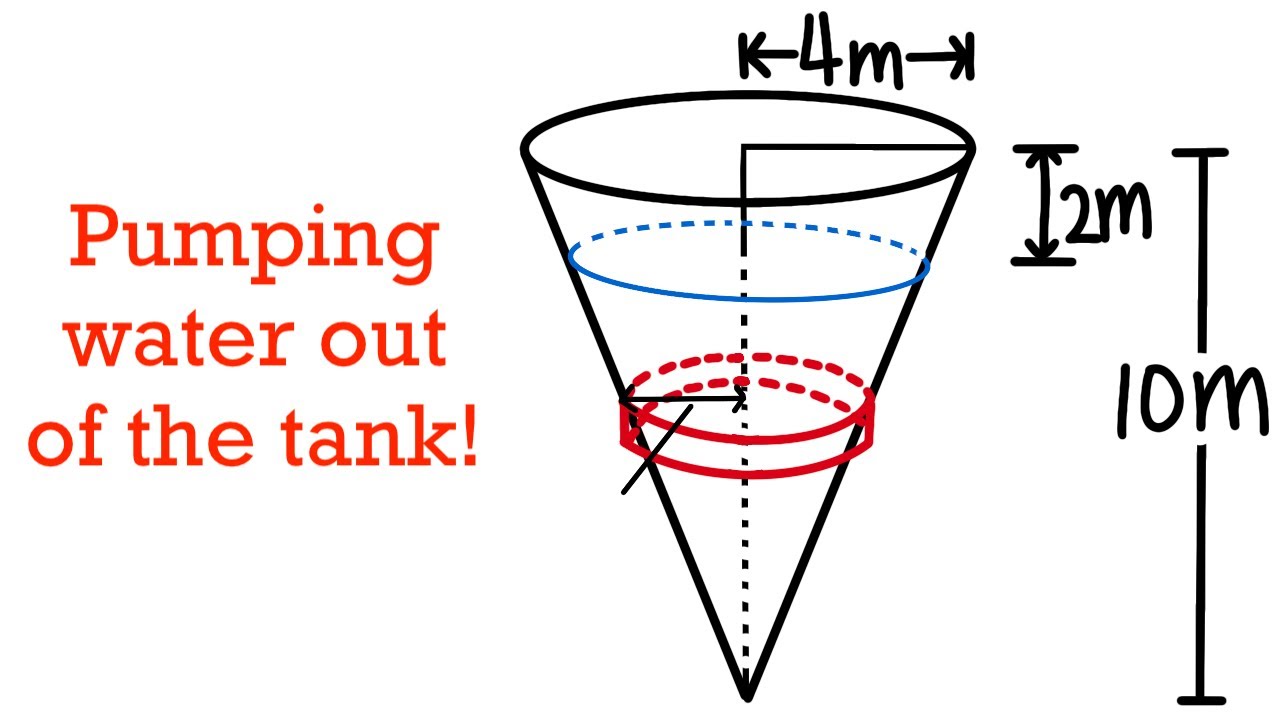
calculating work by using integral, pumping water out of a tank, calculus 2 tutorial

Calculating Work, pumping water out of a tank, calculus 2 tutorial, application of integration

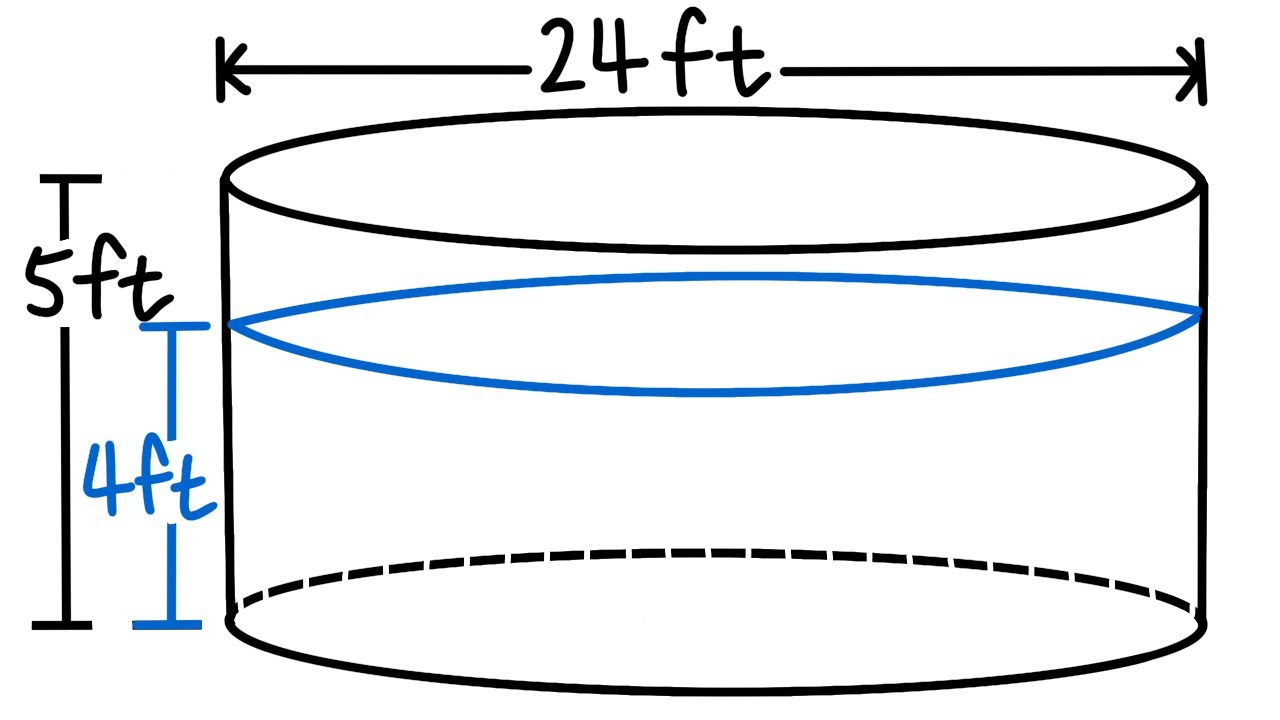
Calculating Work, pumping water out of a circular swimming pool

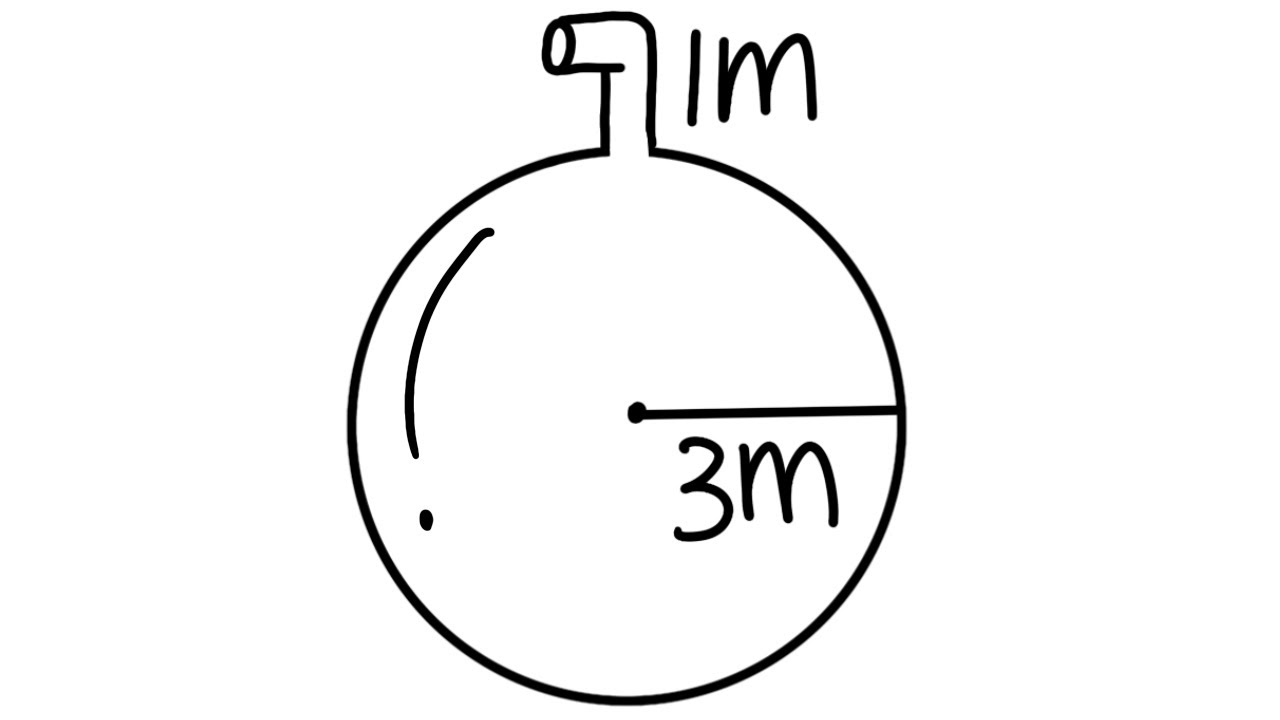
Pumping water out of a spherical tank, calculating work, calculus 2 tutorial

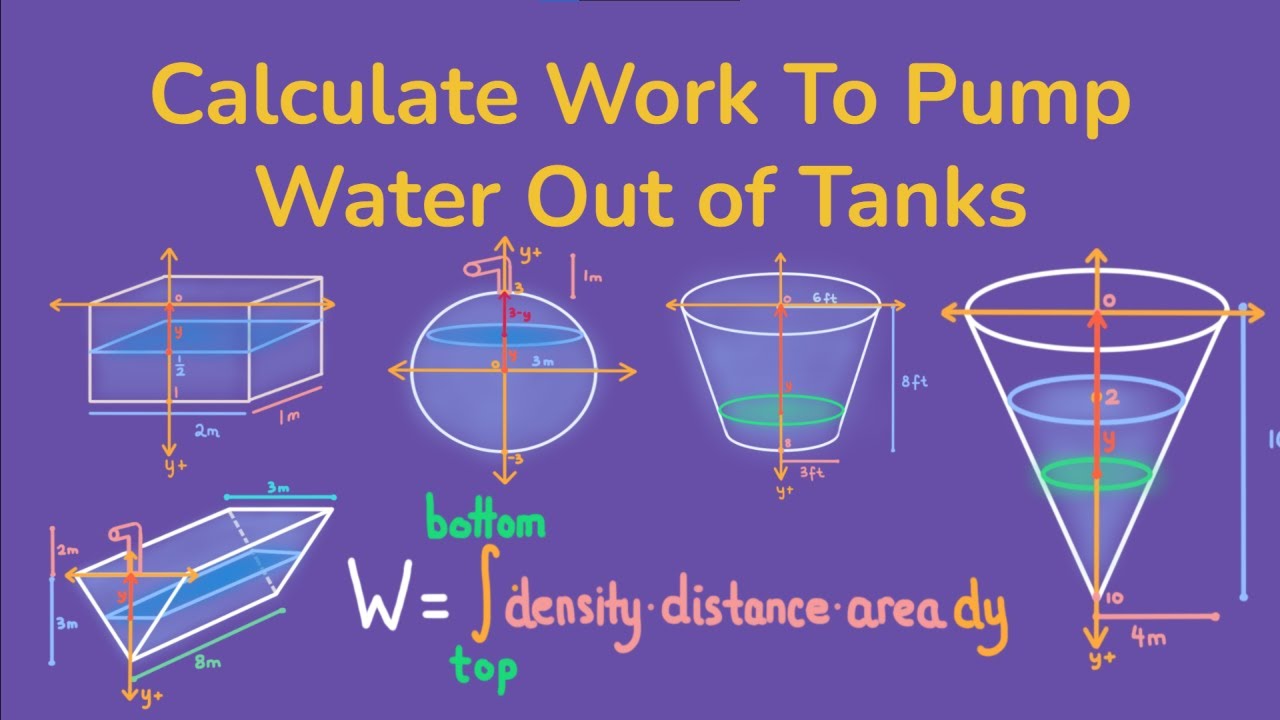
Calculate Work to Pump Liquid Out of Tanks - Calculus 2

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsIntegrationWork CalculationAquariumFluid MechanicsMathematicsDensityForceGravityVolume