Calculate Work to Pump Liquid Out of Tanks - Calculus 2
TLDRThis video tutorial demonstrates how to calculate the work required to pump water out of various tank configurations, including a rectangular aquarium and a three-dimensional sphere. The script explains the steps to set up the problem, including drawing the tank, placing axes, and determining the layers of water to be pumped. It uses integral calculus to find the work, considering factors like water density, distance, and the area of water layers, and provides the formula and calculations for each scenario, resulting in the work measured in joules or foot-pounds.
Takeaways
- 📏 The script discusses calculating work required to pump water out of various tank shapes using integral calculus.
- 📚 The first example involves an aquarium with dimensions of 2m x 1m x 1m, and the work to pump out half the water is calculated.
- 📉 The work formula used is W = ∫(density * distance * area * dy) from the bottom to the top of the water layer.
- 🔍 For the aquarium, the density of water is 9800 kg/m³ (if measured in meters), and the area of water layers is constant at 2m².
- 🧩 The integral for the aquarium example results in a work value of 2450 Joules, representing the energy needed to pump out half the water.
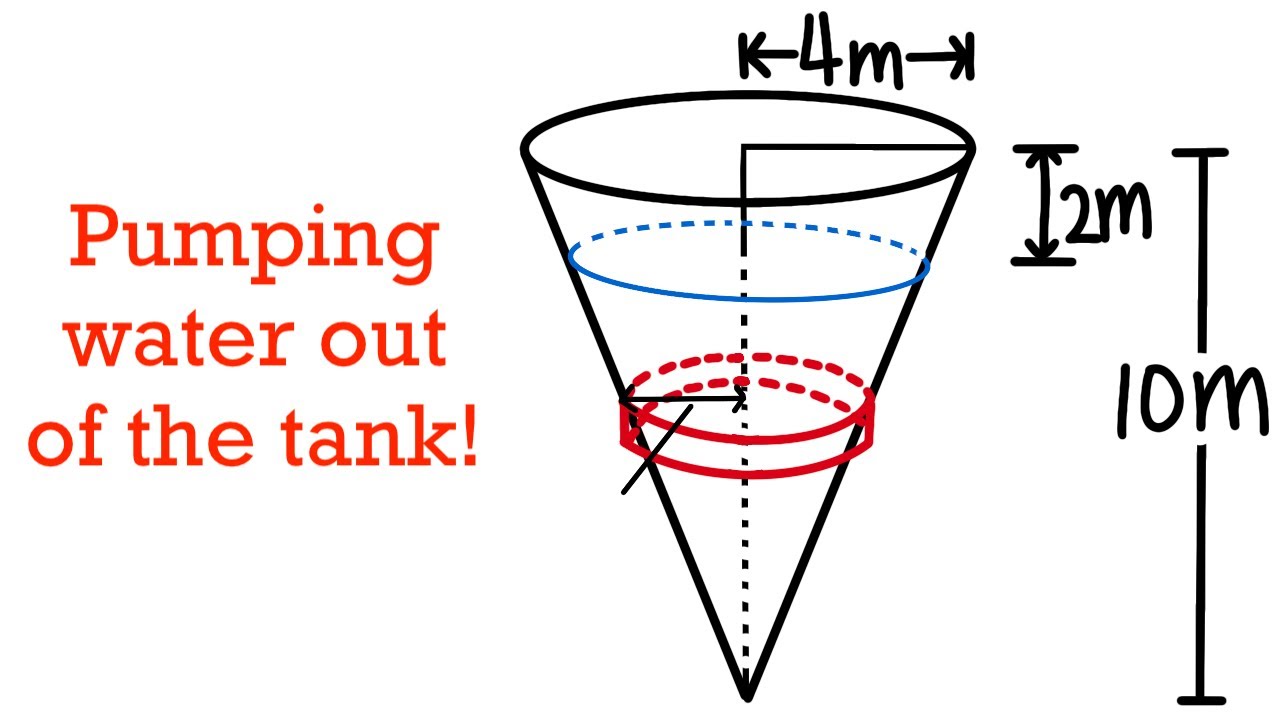
- 🌌 The second example is an inverted circular cone with a height of 10m, a base radius of 4m, and water filled to a height of 8m.
- 📐 The work to empty this tank is calculated by integrating over the volume of water, considering the varying radius with height.
- 📈 The area of water layers in the cone is given by π times the radius squared, which changes with the height y as x² = 25(9 - y²).
- 🌡 The integral for the cone results in a work value of approximately 3.4 x 10^6 Joules.
- 🛢️ Additional examples include a rectangular tank with dimensions of 8m x 3m x 3m, and a three-dimensional sphere with a radius of 3m.
- 📘 Each example follows a similar process of setting up an integral based on the geometry of the tank and the physical properties of water.
- 🔑 The takeaway is that the work required to pump water out of a tank can be calculated using the integral of the product of density, distance, and area over the volume of water.
Q & A
What is the purpose of the video?
-The purpose of the video is to demonstrate how to calculate the amount of work required to pump water out of different types of tanks and containers.
What is the first step in solving the problem of pumping water out of an aquarium?
-The first step is to visualize and draw the aquarium, understanding its dimensions and the volume of water to be pumped out.
How is the work formula applied in the context of pumping water out of a tank?
-The work formula W = ∫(density * distance * area * dy) from the bottom to the top of the tank is used to calculate the work required, where density is the fluid density, distance is the height the water is lifted, and area is the cross-sectional area of the water layer.
What is the significance of the X and Y axes in the script?
-The X and Y axes are used to establish a coordinate system for the tank, which helps in determining the position of each water layer and the corresponding work done in lifting it.
What is the density of water used in the calculations if the problem is given in meters?
-The density of water used in the calculations is 9800 kg/m³ when the problem is given in meters, which is the standard density of water in SI units.
How does the area of the layer of water change when pumping from an aquarium?
-The area of the layer of water remains constant when pumping from an aquarium, as it is the base area of the rectangular tank, which does not change with depth.
What is the difference between calculating work for a rectangular tank and an inverted circular cone?
-For a rectangular tank, the area of the water layer is a rectangle, while for an inverted circular cone, the area of the water layer is a circle, and the radius of this circle changes with depth, requiring integration with respect to the changing radius.
What is the unit of work when the problem is given in meters?
-The unit of work is joules when the problem is given in meters, as it follows the SI unit system for work done.
How does the script handle the calculation of work for a layer of water in a spherical tank?
-The script uses the formula for the area of a circle (π * radius²) and integrates over the volume of the sphere, considering the changing radius and the distance the water is lifted.
What is the final step in calculating the work to pump water out of a tank according to the script?
-The final step is to evaluate the integral of the work formula over the specified range (from the bottom to the top of the water) and simplify the result to find the total work done in joules or other units as appropriate.
Outlines
📏 Calculating Work to Pump Water from an Aquarium
This paragraph outlines the process of calculating the work required to pump half the water out of an aquarium with dimensions of 2 meters in length, 1 meter in width, and 1 meter in depth. The explanation begins with a visual representation of the tank and the establishment of the X and Y axes. It then details the integral formula for work (W), which involves the density of water, the distance each water layer is pumped (y), and the area of each layer. The density is given as 9800 if the dimensions are in meters, with the work unit being joules. The integral calculation is simplified by factoring out constants and integrating the function of y, resulting in a final work calculation of 2450 joules.
🌌 Work Required to Empty a Water-filled Inverted Cone Tank
The second paragraph describes a problem involving an inverted circular cone-shaped tank with a height of 10 meters and a base radius of 4 meters, filled with water to a height of 8 meters. The task is to calculate the work needed to pump all the water out. The explanation includes drawing a diagram, placing the X and Y axes, and determining the layers of water to be pumped. The work formula is reiterated, with the density of water given as 9800 for meters-based dimensions. The area of each water layer is calculated using the formula for the area of a circle, with the radius expressed in terms of x. The paragraph concludes with the integral calculation, resulting in the work required to empty the tank, which is approximately 3.4 x 10^6 joules.
📚 Converting Variables for Work Calculation in a Cone Tank
This paragraph focuses on the mathematical conversion of variables necessary for calculating the work to empty a cone-shaped tank. It begins with the equation of a line derived from two points on the tank's surface. The slope of the line is calculated, and the point-slope form of the line equation is established. The equation is then rearranged to solve for x in terms of y, which is substituted back into the area formula for the water layer. The integral for calculating the work is set up, and the constants are factored out. The antiderivative of the function is found, and the limits of integration from 2 to 10 are applied to find the total work, which is presented as a numerical value.
🚰 Detailed Steps to Calculate Work for a Partially-filled Circular Tank
The fourth paragraph provides a detailed explanation of calculating the work to empty a partially-filled circular tank. It starts with the tank's dimensions and the need to move water layers to the top. The process includes setting up the X and Y axes, drawing a layer of water, and using the formula for work. The density of water and the distance each layer is moved are specified. The area of the water layer is calculated using the radius in terms of x, which is then converted to y. The paragraph concludes with the integral calculation for the work, resulting in a value that is converted to feet-pounds as the unit of work.
🔁 Work Calculation for a Rectangular Tank with a Spout
This paragraph explains the process of calculating the work required to pump water out of a rectangular tank with a spout. It includes placing the X and Y axes, drawing the layers of water, and using the work formula. The density, distance, and area components of the formula are detailed, with the area calculated based on the tank's dimensions. The paragraph concludes with the integral calculation, which accounts for the additional distance the water must travel through the spout, resulting in a final work value in joules.
🌐 Calculating Work for a Spherical Tank using Integrals
The sixth paragraph discusses the calculation of work to pump water out of a three-dimensional spherical tank. It includes setting the X and Y axes at the center of the sphere, visualizing the layers of water, and using the work formula. The distance each layer is moved is adjusted for the spout height. The area of the water layer is expressed in terms of y, and the integral for work is set up. The paragraph concludes with the calculation of the integral and the final work value in joules.
📉 Integral Calculation for Work to Empty a Sphere-shaped Tank
This paragraph focuses on the integral calculation for the work required to empty a sphere-shaped tank. It starts with the tank's dimensions and the establishment of the axes. The distance from the origin to the water layer is expressed as 3 - y. The work formula is applied with the density, distance, and area components. The area is calculated using the Pythagorean relationship between x and y. The integral is set up and evaluated, resulting in a final work value in joules.
🔢 Final Calculation of Work for a Spherical Water Tank
The final paragraph wraps up the series by calculating the work to pump water out of a spherical tank. It reiterates the tank's dimensions and the integral formula for work. The constants are factored out, and the integral is simplified to a polynomial function of y. The antiderivative of this function is found, and the limits of integration are applied to calculate the total work. The final result is presented as a numerical value in joules, representing the work required to empty the tank.
Mindmap
Keywords
💡Work
💡Aquarium
💡Density
💡Integral
💡Area
💡Pumping
💡Axis
💡Volume
💡Spout
💡Three-Dimensional Sphere
Highlights
Introduction to calculating work required to pump water out of a tank.
Aquarium dimensions provided: 2m long, 1m wide, 1m deep.
Explanation of the process to pump half the water out of the aquarium.
Drawing and understanding the X and Y-axis orientation for the problem.
Calculation of work using the integral formula with density, distance, and area.
Use of density values based on units of measurement (meters or feet).
Integration of the area of water layers in the form of rectangles.
Solving the integral to find the work needed in joules.
Introduction to a problem involving an inverted circular cone tank.
Description of the cone tank's dimensions and water level.
Method to convert variables from X to Y for the cone tank problem.
Calculation of work for the cone tank using the area of circular layers.
Integration of the area formula derived from the cone's geometry.
Final work calculation for emptying the cone tank expressed in joules.
Presentation of a tank problem with a rectangular shape and a spout.
Strategy to calculate work by considering the tank's dimensions and spout height.
Conversion of the base of the water layer from X to Y for integration.
Final calculation of work to pump water out of the rectangular tank with a spout.
Introduction to calculating work for a three-dimensional sphere tank.
Understanding the geometry of the sphere and the spout's impact on work calculation.
Derivation of the area formula for spherical layers of water.
Integration of the spherical layer area in the work formula.
Final work calculation for the sphere tank in joules.
Transcripts
Browse More Related Video

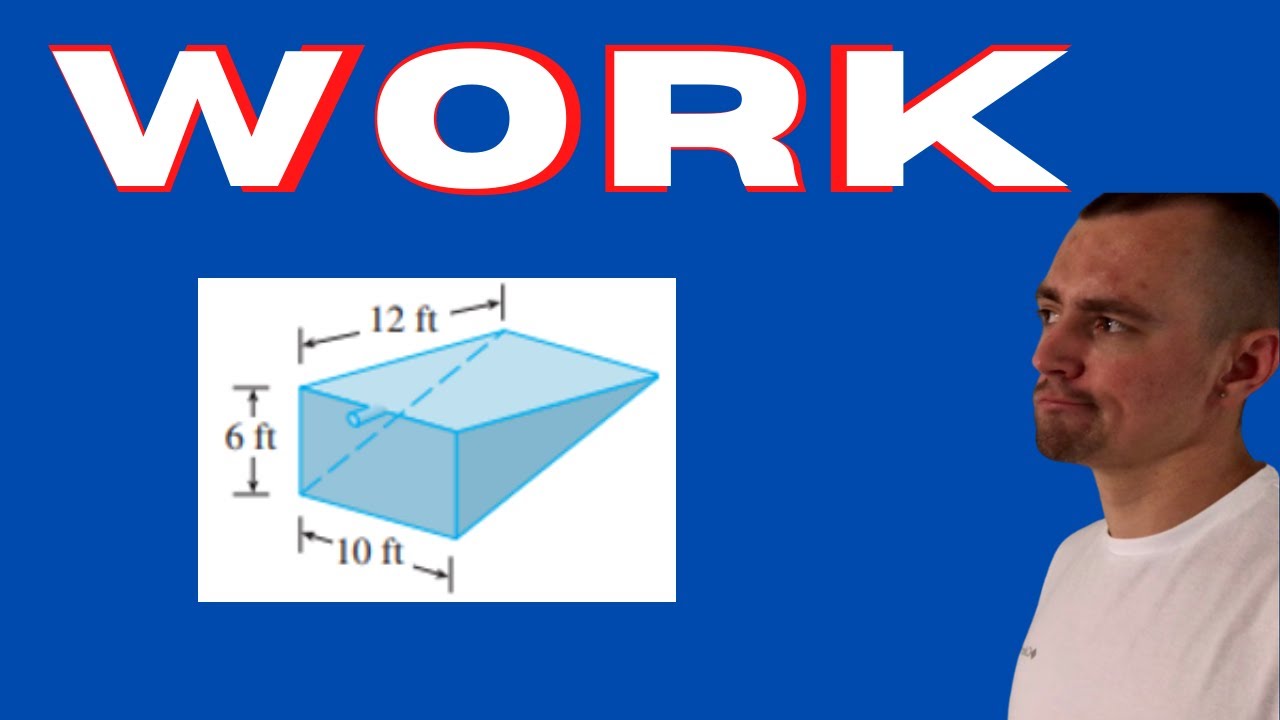
Calculate Work to Pump Water Out of Rectangular Tank
calculating work by using integral, pumping water out of a tank, calculus 2 tutorial

Calculating Work, pumping water out of a tank, calculus 2 tutorial, application of integration
FIND THE WORK REQUIRED TO PUMP THE WATER OUT OF THE TANK
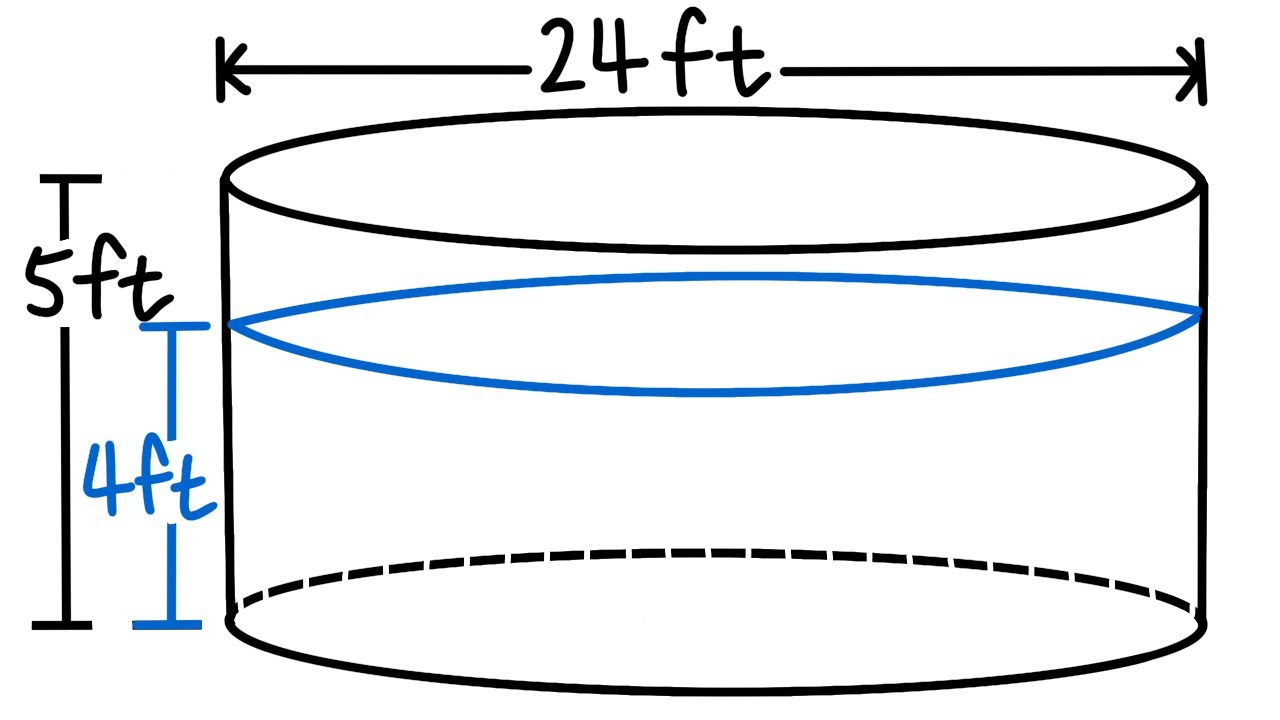
Calculating Work, pumping water out of a circular swimming pool
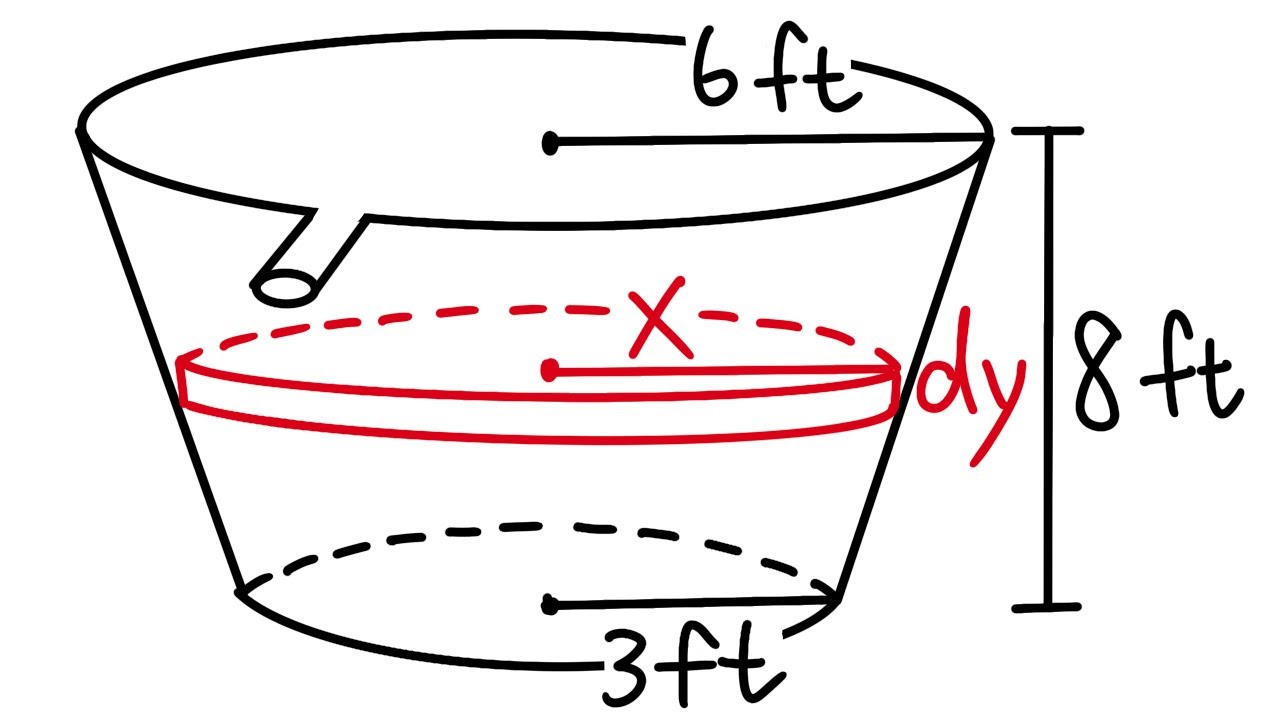
Pumping water out of a bucket, calculating work, calculus 2 tutorial
5.0 / 5 (0 votes)
Thanks for rating: