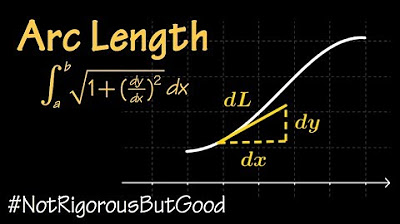Find the Arc Length of a Function with Calculus
TLDRThis educational video tutorial demonstrates how to calculate the arc length of a function between two points, using integral calculus. It introduces two formulas, one based on the derivative with respect to x and the other with respect to y, and illustrates the process with examples, including simplifying the integrand and applying the fundamental theorem of calculus. The video concludes with finding the arc length of a function in terms of y, showcasing a step-by-step approach to simplify complex integrals and solve them accurately.
Takeaways
- 🔢 The video demonstrates how to find the arc length of a function.
- 📐 The horizontal line example shows a length of 4 from point 2 to 6.
- 🧮 Arc length formulas: L = ∫(A to B) √(1 + (f'(x))²) dx and L = ∫(A to B) √(1 + (f'(y))²) dy.
- 📊 Example function: y = (2/3)x^(3/2) between 0 and 2.
- 🔍 Derivative of the function: f'(x) = x^(1/2), and (f'(x))² = x.
- 📏 Integrating from 0 to 2: use fundamental theorem of calculus and substitution.
- 🔄 Substitution: u = x + 1, and the integral is solved to find the arc length.
- 🧩 Second example: y = (2/3)(x² + 1)^(3/2) between 0 and 1.
- 📈 Simplification trick: convert integrals into a more manageable form using algebraic manipulation.
- 📝 Final example: find arc length of a function in terms of y between 1 and 2 using similar steps.
Q & A
What is the main topic of the video?
-The main topic of the video is how to find the arc length of a function between two points, A and B.
What are the two formulas provided in the video for calculating arc length?
-The two formulas provided are: L = ∫(A to B) √(1 + (f'(x))^2) dx and L = ∫(A to B) √(1 + (f'(y))^2) dy.
What is the first function given as an example in the video?
-The first function given as an example is y = (2/3) * (x^(3/2)) between 0 and 2.
How do you find the derivative of the first example function?
-The derivative of the first example function, f'(x), is found by differentiating (2/3) * (x^(3/2)), which results in x^(1/2).
What is the integral formula used to find the arc length of the first example function?
-The integral formula used is L = ∫(0 to 2) √(1 + x) dx.
What substitution method is used in the video to simplify the integral of the first example function?
-The substitution method used is u-substitution, where u is set to x + 1, thus du/dx = 1 and dx = du.
What is the final simplified form of the integral for the first example function?
-The final simplified form of the integral for the first example function is 2/3 * (x + 1)^(3/2) + C.
What is the second function given as an example in the video?
-The second function given as an example is y = (2/3) * (x^2 + 1)^(3/2) between 0 and 1.
How is the derivative of the second example function simplified in the video?
-The derivative of the second example function is simplified to 4x * (x^2 + 1)^(1/2), and then squared to get 4x^2 * (x^2 + 1).
What is the integral formula used to find the arc length of the second example function?
-The integral formula used is L = ∫(0 to 1) √(1 + 4x^2 * (x^2 + 1)) dx.
What is the trick mentioned in the video to simplify the integral of the second example function?
-The trick is to simplify the integral into the form √(a + b^2), which simplifies the calculation by removing the square root.
What is the third function given as an example in the video, and how is it different from the first two?
-The third function is given in terms of y, f(y) = y^4/8 + y^(-2)/4, and it is different because it requires using the formula L = ∫(A to B) √(1 + (f'(y))^2) dy for calculation.
How is the derivative of the third example function found in the video?
-The derivative of the third example function, f'(y), is found by differentiating the terms y^4/8 and y^(-2)/4, resulting in 1/2 * y^3 and -1/2 * y^(-3).
What is the final result of the arc length for the third example function between y = 1 and y = 2?
-The final result of the arc length for the third example function between y = 1 and y = 2 is 33/60.
Outlines
📚 Introduction to Arc Length Calculation
This paragraph introduces the topic of the video, which is finding the arc length of a function between two points, A and B. The presenter illustrates the concept with a blue function and a pink reference line, emphasizing the need for formulas when dealing with the blue line. Two integral formulas are presented for calculating arc length, depending on whether the function is given in terms of x or y. The paragraph concludes with an example of finding the arc length of the function y = (2/3) * x^(3/2) from 0 to 2, including the process of finding the derivative and setting up the integral.
🔍 Detailed Example: Arc Length of a Function in Terms of X
The second paragraph delves into a detailed example of calculating the arc length of a function given in terms of x. The function in question is y = (2/3) * x^2 + 1^(3/2), with the range from 0 to 1 on the x-axis. The presenter explains the process of finding the derivative of the function, squaring it, and simplifying the resulting expression. A trick for simplifying the integral by expressing it in the form of a + b^2 is introduced, followed by the application of the fundamental theorem of calculus to find the final answer, which is the length of the function between the specified points.
📐 Advanced Example: Arc Length of a Function in Terms of Y
This paragraph presents an advanced example of calculating the arc length for a function given in terms of y, specifically f(y) = y^4/8 + 1/4 * y^(-2). The range considered is from y = 1 to y = 2. The presenter outlines the process of rewriting the function, finding the derivative with respect to y, and squaring the derivative to prepare for the integral. A method for simplifying the integral by expressing it in the form of a + b^2 is detailed, leading to the calculation of the integral using the fundamental theorem of calculus and arriving at the arc length.
🎉 Conclusion and Call to Action
In the final paragraph, the presenter concludes the video with a summary of the process for finding the arc length of a function, both in terms of x and y. The presenter encourages viewers to ask questions in the comments section and to subscribe and like the video if they found it helpful. The paragraph ends with a light-hearted note about buying the presenter a cup of coffee, emphasizing the value of viewer support.
Mindmap
Keywords
💡Arc Length
💡Function
💡Integral
💡Derivative
💡Fundamental Theorem of Calculus
💡Square Root
💡U-Substitution
💡Chain Rule
💡Antiderivative
💡Power of a Number
Highlights
Introduction to the method for finding the arc length of a function between two points.
Explanation of using the horizontal distance as an easy method for arc length when possible.
Introduction of two formulas for calculating arc length: one using the derivative with respect to x and the other with respect to y.
Demonstration of finding the arc length of the function y = (2/3) * x^(3/2) between 0 and 2.
Derivation of the formula for arc length in terms of x by taking the derivative and squaring it.
Use of the fundamental theorem of calculus to evaluate the integral for arc length.
Application of u-substitution to simplify the integral of the square root of 1 + x.
Calculation of the final answer for the arc length of the given function between 0 and 2.
Presentation of a second example to find the arc length of y = (2/3) * x^2 + 1^(3/2) between 0 and 1.
Derivation of the formula for arc length in terms of x for the second example, including simplification.
Introduction of a trick to simplify the integral by converting it into a + b^2 form.
Calculation of the arc length for the second function using the simplified integral form.
Introduction of a third example with a function in terms of y to find the arc length between 1 and 2 on the y-axis.
Derivation of the formula for arc length in terms of y, including the derivative with respect to y.
Simplification of the integral by converting the expression under the square root into a + b^2 form.
Final calculation of the arc length for the function in terms of y between 1 and 2 on the y-axis.
Conclusion summarizing the process and results of finding arc lengths for the given functions.
Invitation for viewers to ask questions and engage with the content in the comments section.
Encouragement for viewers to subscribe, like, and support the channel for more educational content.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: