Work Done Raising a Leaky Bucket with an Integral
TLDRIn this educational script, Phil tackles a physics word problem involving lifting a leaky bucket. The bucket, initially weighing 15 pounds and containing 10 pounds of water, is raised 20 feet at a constant speed. The rope's weight density is 0.3 pounds per foot. As the bucket leaks, its weight decreases linearly to 10 pounds. Phil breaks down the problem into calculating work done on the rope and the bucket separately, using integral calculus to find the total work, which sums up to 310 foot-pounds, highlighting the concept of variable force in work calculations.
Takeaways
- 📐 The problem involves calculating the work done to raise a 5-pound bucket filled with water, which leaks during the process.
- 🚰 The bucket starts with 10 pounds of water and has 5 pounds remaining when it reaches the top, implying a constant leak rate.
- 🪢 The rope's weight is 0.3 pounds per foot, which is considered in the calculation of the work done to lift the rope itself.
- 🔍 The problem is broken down into two parts: the work done on the rope and the work done on the bucket, simplifying the analysis.
- ⚖️ The force on each 'slice' of the rope is calculated by multiplying its length by the rope's density.
- 📈 The work done on the rope is found by integrating the force over the distance from the top to the bottom of the 20-foot lift.
- 📉 The bucket's weight changes linearly as it loses water, creating a variable force that needs to be integrated over the lift.
- 📚 The work done on the bucket is calculated by setting up an integral based on the linear decrease in the bucket's weight.
- 📉 The integral for the bucket's work considers the change in weight from 15 pounds at the bottom to 10 pounds at the top.
- 🧮 The total work done is the sum of the work done on the rope and the bucket, which is calculated separately and then added together.
- 🔑 The final result of the work done to raise the bucket, considering both the rope and the leaking water, is 310 foot-pounds.
Q & A
What is the main problem discussed in the script?
-The script discusses a physics problem involving calculating the work done to raise a leaky bucket filled with water, attached to a rope of a certain weight per foot, over a distance of 20 feet at a constant speed.
What is the weight of the bucket in the problem?
-The bucket initially weighs 5 pounds but starts with 10 pounds of water, and by the time it reaches the top, there are 5 pounds of water left.
What is the weight of the rope per foot?
-The rope weighs 0.3 pounds per foot, which is its density.
What is the method used to calculate the work done on the rope?
-The work done on the rope is calculated by integrating the force exerted on each slice of the rope over the distance from 0 to 20 feet.
How is the work done on the ith slice of the rope calculated?
-The work on the ith slice of the rope is calculated by multiplying the force on the ith slice (0.3 * delta x) by the distance it is moved (x sub i).
What is the integral used to find the work done on the rope?
-The integral used to find the work done on the rope is the integral of 0.3 * x dx from 0 to 20.
What is the result of the integral for the work done on the rope?
-The result of the integral for the work done on the rope is 60 foot-pounds.
How does the weight of the bucket change as it is being lifted?
-The weight of the bucket changes linearly as it loses water at a constant rate, starting at 15 pounds when not lifted at all and decreasing to 10 pounds when it reaches the top.
What is the formula used to calculate the force on the bucket at any given height?
-The formula used to calculate the force on the bucket at any given height is 1/4 * x sub i + 10, where x sub i is the height in feet.
What is the integral used to find the work done on the bucket?
-The integral used to find the work done on the bucket is the integral of (1/4 * x + 10) dx from 0 to 20.
What is the total work done to raise the bucket and the rope?
-The total work done to raise the bucket and the rope is the sum of the work done on the rope (60 foot-pounds) and the work done on the bucket (250 foot-pounds), which equals 310 foot-pounds.
Outlines
🔍 Calculating Work Done on a Leaking Bucket
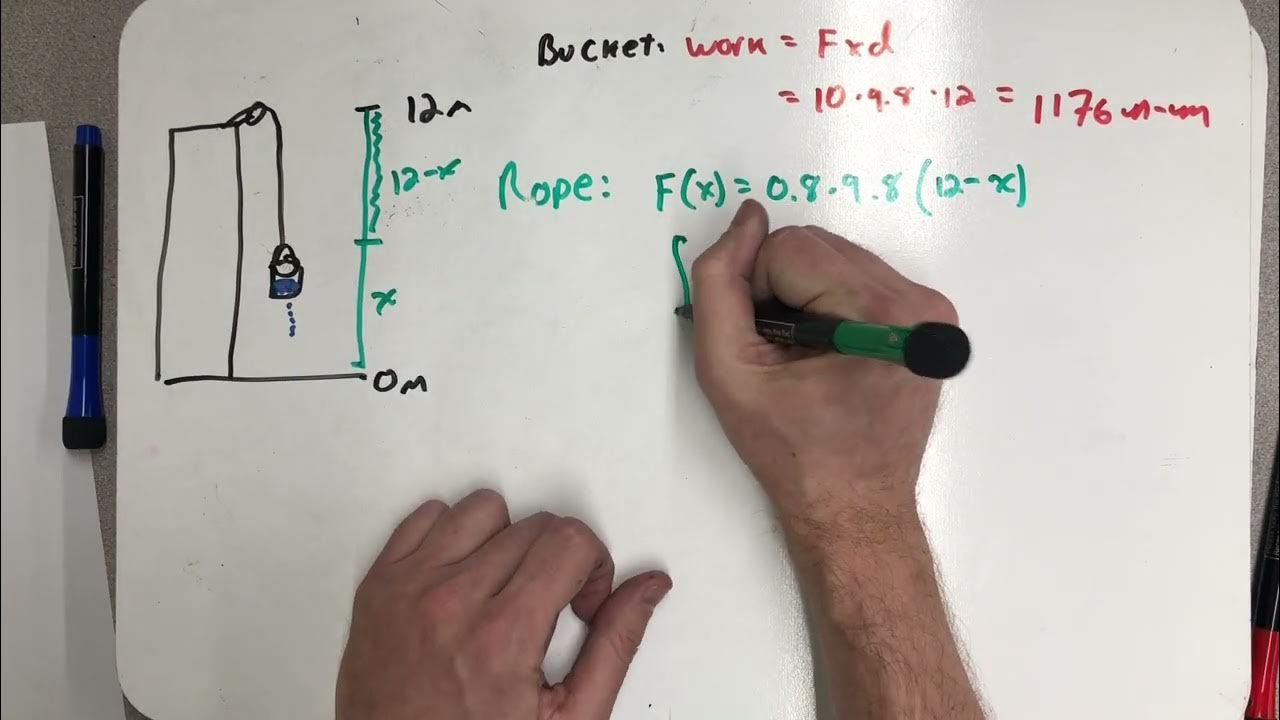
In this paragraph, Phil introduces a physics problem involving a five-pound bucket with a rope that weighs 0.3 pounds per foot. The bucket is lifted 20 feet at a constant speed, starting with 10 pounds of water, leaking until only 5 pounds remain at the top. The focus is on calculating the work done to raise the bucket. The explanation involves breaking down the problem into two parts: the rope's weight and the bucket's changing weight due to the leak. For the rope, the work is calculated using an integral of the force (0.3 pounds per foot) over the 20-foot distance. For the bucket, the work is more complex due to the variable weight as water leaks out, requiring a linear relationship between the bucket's weight and the height it is lifted.
📐 Work Calculation for a Leaking Bucket and Rope
This paragraph continues the explanation of the work done to raise the bucket. It details the process of calculating the work for both the rope and the bucket separately. For the rope, the work is calculated as an integral of the force over the distance, resulting in 60 foot-pounds. For the bucket, a linear equation is derived from the initial and final weights at different heights, leading to a calculation of work done as the bucket loses water. The work for the bucket is calculated as an integral of the force over the distance, yielding 250 foot-pounds. The total work done to raise both the rope and the bucket is then summed up to be 310 foot-pounds, providing a comprehensive solution to the problem.
Mindmap
Keywords
💡Work
💡Leaky Bucket
💡Constant Speed
💡Rope Density
💡Integral
💡Slice
💡Linear Relationship
💡Foot-Pounds
💡Force
💡Distance
Highlights
Introduction of a word problem involving a standard scenario of lifting a leaky bucket.
The bucket's weight is 5 pounds, and it is lifted 20 feet at a constant speed.
The rope's weight is 0.3 pounds per foot, emphasizing its density in the calculation.
The bucket initially contains 10 pounds of water, which leaks during the lift.
By the time the bucket reaches the top, only 5 pounds of water remain.
The problem is broken down into calculating work done for the rope and the bucket separately.
For the rope, the force on each slice is calculated based on its length and density.
The work done on each slice of the rope is the product of its force and the distance moved.
An integral is used to calculate the total work done on the rope over the 20-foot distance.
The integral's limits are from the top (0) to the bottom (20 feet) of the lift.
The work done to raise just the rope is calculated to be 60 foot-pounds.
The bucket's force changes due to the water leaking, requiring a dynamic calculation.
A linear relationship is established between the bucket's weight and its height during the lift.
The force on the bucket is calculated as a function of its height, accounting for the water loss.
The work done on the bucket is also calculated using an integral, with similar limits as the rope.
The total work done to raise the bucket, considering the water leakage, is 250 foot-pounds.
The final step is to add the work done on the rope and the bucket to get the total work.
The total work done to raise the bucket and rope is calculated to be 310 foot-pounds.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: