Calculating the Work Required to Drain a Tank

patrickJMT
14 Sept 200810:27
EducationalLearning
32 Likes 10 Comments

TLDRThis video tutorial explores the concept of work in the context of draining a triangular tank, using James Stewart's calculus textbook as a reference. It explains the work formula as the integral of force times displacement and guides through the process of calculating the volume of a cross-sectional slice, determining the force on the water, and setting up the integral with appropriate limits. The video uses similar triangles to express the width of the slice in terms of depth and illustrates the displacement needed for the water to exit the tank, providing a clear methodology for solving work-related calculus problems.

Takeaways
  • 📚 The video discusses a work problem from a calculus textbook, specifically using James Stewart's calculus book.
  • 🔍 It focuses on the work required to drain a tank, explaining the concept of work as the integral of force times displacement.
  • 📐 The general procedure for tank problems involves finding the volume of a generic cross-sectional slice of the tank.
  • 💧 The force is calculated using the density of water and the dimensions of the cross-sectional slice.
  • 📏 The example tank is triangular with a width and height of three feet, and a spout two feet tall.
  • 📉 The video demonstrates how to calculate the volume of a generic cross-sectional slice by approximating it as a box with variable width.
  • 📐 The width of the slice is determined using similar triangles, relating it to the depth 'X' from the top of the tank.
  • 🔢 The force on the slice of water is calculated by multiplying the volume of the slice by the density of water and the acceleration due to gravity.
  • 🚀 The displacement of the water is the sum of the depth 'X' and the height of the spout, which is two feet in this case.
  • ∫ The final step is to set up and evaluate the integral with the correct limits of integration, from the top (0) to the bottom (3 feet) of the tank.
  • 📝 The video emphasizes the importance of understanding the geometry of the problem and setting up the integral correctly for solving work problems related to draining tanks.
Q & A

  • What are the three types of work problems mentioned in the video?

    -The three types of work problems mentioned are tank problems, spring problems, and cable/rope problems.

  • What is the general procedure for solving tank problems as described in the video?

    -The general procedure involves finding the volume of a generic cross-sectional slice, calculating the force by multiplying the volume by the density of water (adjusted for units), determining the displacement, and then integrating the force times displacement over the limits of integration.

  • How is force calculated when the units are in feet?

    -When the units are in feet, force is calculated by multiplying the volume by 62.5 pounds, which is the weight density of water in pounds per cubic foot.

  • How is force calculated when the units are in meters?

    -When the units are in meters, force is calculated by multiplying the volume by 9.81 times 1000, which accounts for the density of water and the acceleration due to gravity in the metric system.

  • What are the dimensions of the triangular tank described in the problem?

    -The triangular tank is 10 feet long, with a height and width of 3 feet at the top. It also has a spout that is 2 feet tall.

  • How is the cross-sectional slice of the tank described in the video?

    -The cross-sectional slice is a thin slab of water taken from a certain depth (X units) from the top of the tank. It has a height of Delta X, a length of 10 feet (the length of the tank), and a width that varies depending on the depth X.

  • How is the width of the cross-sectional slice expressed in terms of X?

    -The width of the cross-sectional slice is determined using similar triangles. It is expressed as W = 3 - X, where X is the depth from the top of the tank.

  • What is the formula for the volume of the cross-sectional slice?

    -The volume of the cross-sectional slice is given by the formula 10 * (3 - X) * Delta X.

  • How is the displacement of the water slice calculated?

    -The displacement of the water slice is calculated as 2 + X, where X is the depth from the top of the tank and 2 is the height of the spout.

  • What are the limits of integration for this problem?

    -The limits of integration are from 0 to 3, where 0 is the top of the tank and 3 is the bottom of the tank.

Outlines
00:00
📚 Introduction to Calculus Work Problems

This paragraph introduces the topic of work problems in calculus, specifically focusing on the types of problems found in James Stewart's popular calculus textbook. The speaker outlines the general procedure for solving tank problems, which involves calculating the work required to drain a tank. The process includes finding the volume of a cross-sectional slice of the tank, determining the force exerted by the water using its density and gravity, and integrating this force over the displacement. The example given is of a triangular tank with specific dimensions, and the speaker explains the initial steps to set up the problem, including defining variables and considering the geometry of the tank.

05:04
📐 Calculating the Volume and Force of a Triangular Tank Slice

The speaker continues the discussion on tank problems by focusing on calculating the volume of a generic cross-sectional slice of a triangular tank. The volume is approximated as a rectangular box, with the length being constant at 10 feet and the width varying with the depth (X) from the top of the tank. Using similar triangles, the width is expressed in terms of X as (3 - X). The force on the water slice is then calculated using the volume and the density of water, considering the units in feet. The displacement required for the water to exit the tank is also discussed, taking into account the height of the tank and the spout. The integral to calculate the work is set up, with the limits of integration ranging from the top to the bottom of the tank.

10:06
🔍 General Strategy for Solving Volume Problems in Calculus

In the final paragraph, the speaker summarizes the general strategy for solving volume problems in calculus, emphasizing that the main variation between problems is the geometry involved. The speaker mentions that for cylindrical tanks, the Pythagorean theorem is often used to set up the radius generically, while for rectangular tanks, the volume is calculated using the straightforward formula of length times width times height. The speaker concludes by encouraging viewers to reach out with questions and wishing them luck in their studies.

Mindmap
Keywords
💡Work
In the context of physics and calculus, 'work' is defined as the product of force and displacement in the direction of the force. In the video, work is used to describe the effort required to drain a tank, which is calculated by integrating the force exerted on a fluid (in this case, water) over the distance it is displaced.
💡Integral
An 'integral' in calculus represents the process of finding the area under a curve, which in this video is used to calculate the total work done in draining the tank. The integral is the mathematical operation that sums up the small bits of work done on each infinitesimal slice of water as it is displaced.
💡Force
In physics, 'force' is any interaction that causes an object to change its velocity. In the script, force is calculated using the weight of the water in a slice, which is the product of its volume, the acceleration due to gravity, and the density of water.
💡Displacement
'Displacement' refers to the change in position of an object. In the video, displacement is the distance a slice of water must travel from its position in the tank to the point outside the tank where it is drained, which includes the vertical distance from the tank's bottom to the spout plus the height of the spout.
💡Tank Problems
The term 'tank problems' in the video refers to a category of calculus problems that involve calculating work done in relation to a container's geometry, such as draining a tank. The video specifically discusses the work required to drain a triangular tank.
💡Cross-Sectional Slice
A 'cross-sectional slice' is a portion of an object that is cut perpendicular to a certain axis, revealing its internal structure. In the context of the video, the cross-sectional slice represents a thin layer of water within the tank, whose volume and force are calculated to determine the work done on it.
💡Volume
The 'volume' of an object or space is the measure of its size in three dimensions. In the video, the volume of a generic cross-sectional slice of the tank is calculated to find the amount of water it contains, which is essential for determining the force exerted on that slice.
💡Density
'Density' is defined as mass per unit volume. In the script, the density of water is used to convert the volume of a water slice into its mass, which is then used to calculate the force due to gravity acting on it.
💡Similar Triangles
The concept of 'similar triangles' is used in the video to express the width of a water slice in terms of its depth (X) from the top of the tank. By recognizing the proportionality between the heights and widths of two triangles, the width of the water slice can be determined as a function of X.
💡Limits of Integration
The 'limits of integration' in calculus define the interval over which an integral is evaluated. In the video, the limits are set from the top to the bottom of the tank (from 0 to 3 feet), indicating the range over which the work to drain the tank is calculated.
💡Triangular Tank
A 'triangular tank' is a container with a triangular cross-section. In the video, the tank's geometry is crucial for determining the volume of the water slices and, subsequently, the work required to drain it. The tank's dimensions and the method for calculating the width of the slices are discussed.
Highlights

Introduction to work problems in calculus, specifically focusing on tank problems.

Explanation of the three main types of work problems: tank, spring, and cable rope problems.

Definition of work as the integral of force times displacement.

General procedure for tank problems involves finding the volume of a generic cross-sectional slice.

Units and force calculation using the density of water and gravitational acceleration.

Description of a triangular tank with specific dimensions for the problem example.

Process of creating a generic cross-sectional slice from the top of the tank.

Approximation of the volume of the slice as a rectangular box with variable width.

Use of similar triangles to express the width of the slice in terms of the depth X.

Expression of the volume of the slice as a function of X.

Calculation of force on the slice using the units in feet and the density of water.

Determination of displacement for the slice of water to be drained.

Integration of force and displacement to calculate the work required to drain the tank.

Identification of limits of integration from the top to the bottom of the tank.

Discussion on the variability of the geometry in different tank problems.

Emphasis on the importance of geometry in setting up the radius or dimensions for integration.

Conclusion summarizing the approach to solving volume problems in calculus.

Invitation for viewers to ask questions via email for further clarification.

Transcripts

Browse More Related Video

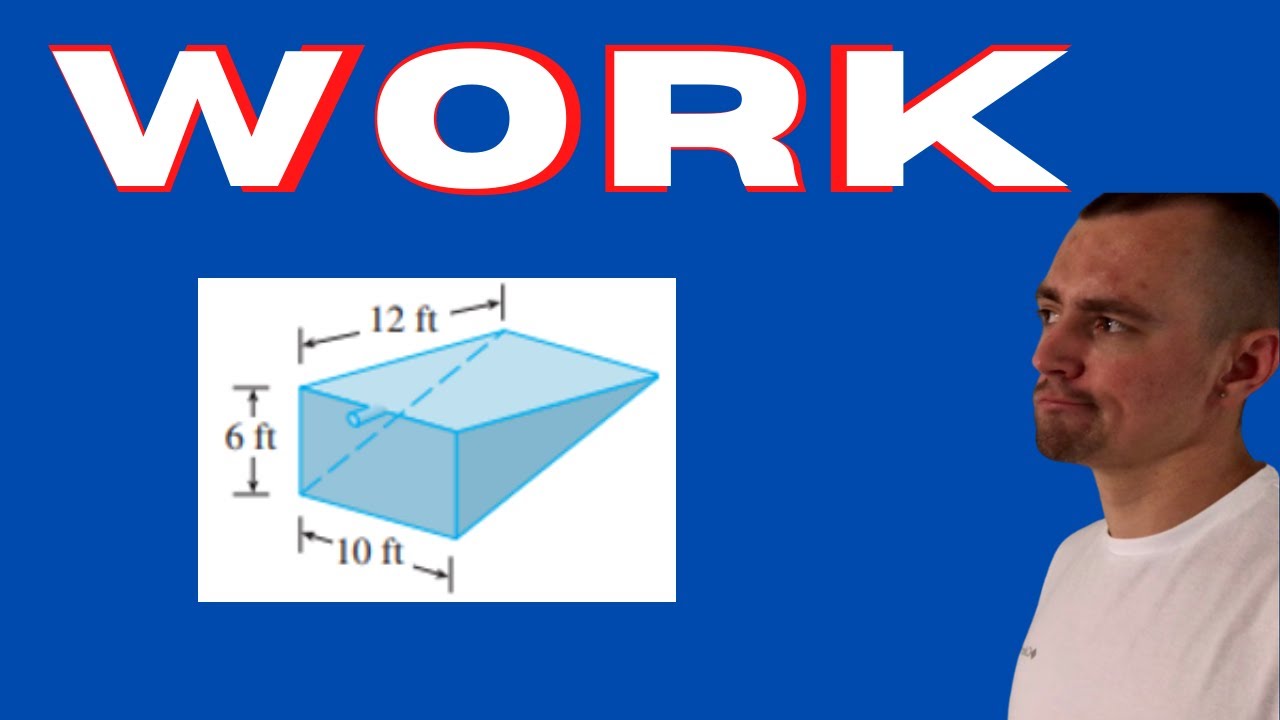
FIND THE WORK REQUIRED TO PUMP THE WATER OUT OF THE TANK

Pumping water out of a spherical tank, calculating work, calculus 2 tutorial

calculating work by using integral, pumping water out of a tank, calculus 2 tutorial

calculating work, pumping water out of a rectangular tank, calculus 2 tutorial

Calculating Work, pumping water out of a tank, calculus 2 tutorial, application of integration

Calculate Work to Pump Water Out of Rectangular Tank

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusWork ProblemTriangular TankVolumeForceDisplacementIntegrationJames StewartEducational ContentPhysicsMathematics