Pumping water out of a bucket, calculating work, calculus 2 tutorial

blackpenredpen
25 Apr 201508:25
EducationalLearning
32 Likes 10 Comments

TLDRIn this video, we calculate the work needed to pump water from a tank shaped like a bucket. We start by using the formula for work, force times distance, where force is derived from the weight of the water. We break the tank into horizontal slices, each resembling a disc, and find the volume by integrating the area of each disc. Using the weight density of water (62.5 lb/ft³), we derive the volume formula involving the radius and thickness of each disc. Finally, we integrate this over the height of the tank to find the total work required.

Takeaways
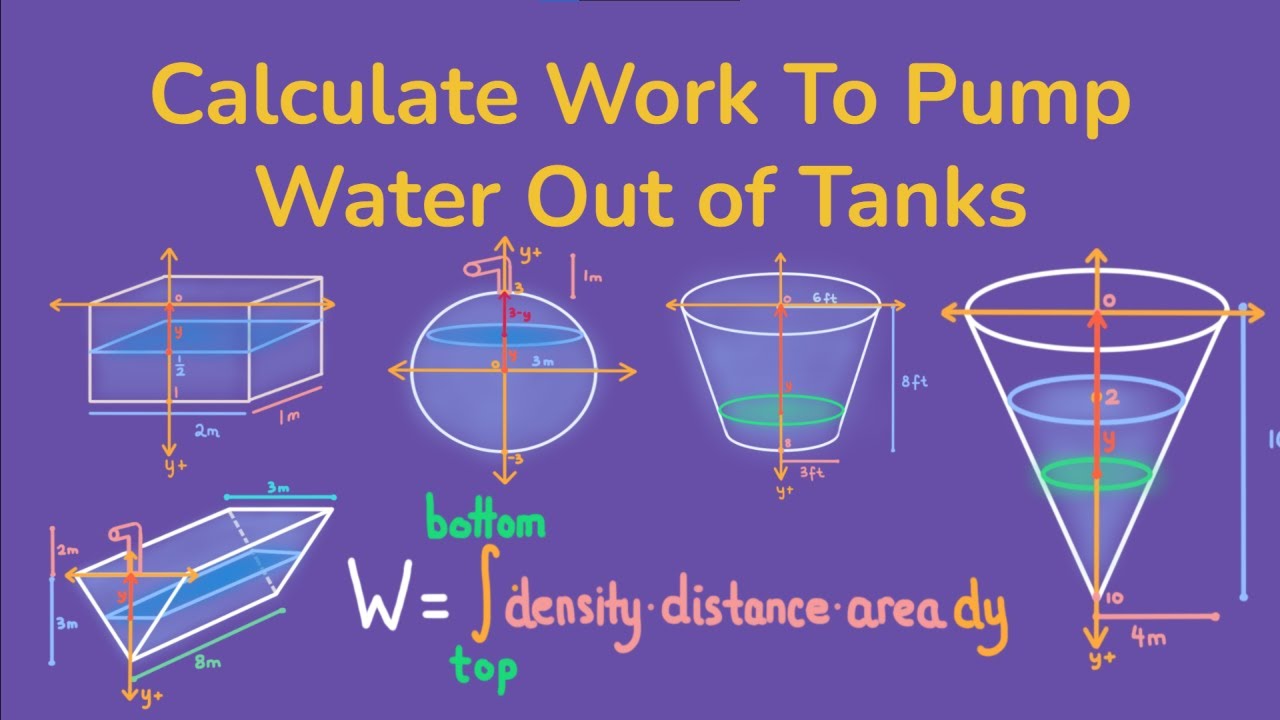
  • 🔍 The video script discusses calculating the work needed to pump water out of a cylindrical tank with a trapezoidal top.
  • 📐 The formula for work involves force times distance, with force being the weight of the water, which depends on its volume and density.
  • 🇺🇸 The script specifies the use of US customary units, with the weight density of water given as 62.5 pounds per cubic foot.
  • 📏 The volume calculation is the most challenging part and involves determining the shape and dimensions of the tank, described as a circular disc with a small thickness.
  • 📉 The tank's shape is likened to a CD, with varying slices of different sizes due to the changing radius from top to bottom.
  • 📊 The radius (X) and vertical thickness (Dy) are defined to calculate the volume of each disk-shaped slice of the tank.
  • 📈 A reference frame is set up to determine the relationship between the radius (X) and the vertical position (Y), using the dimensions of the trapezoidal top.
  • ✍️ The equation of the line that represents the sloping edge of the tank is derived from two known points, with a slope of 8/3.
  • 📝 Algebra is used to isolate X in terms of Y, resulting in the formula X = (3/8)Y + 3, which is essential for calculating the volume of the tank.
  • 🔄 The volume of the tank is calculated using the formula for the volume of a disk, π * (r^2) * thickness, with r being the function of Y found earlier.
  • 🚰 The work to pump out each disk of water is calculated by integrating the force over the distance each disk must travel, from the bottom to the top of the tank.
  • 📉 The distance each disk travels is represented by (8 - Y), where Y varies from 0 to 8, indicating the height of the tank.
Q & A

  • What is the primary formula used to calculate work in this context?

    -The primary formula used to calculate work in this context is force times distance. The force is essentially the weight of the water, which is determined by its volume and density.

  • Why is the density of water important in this calculation?

    -The density of water is important because it is used to convert the volume of water into its weight. The weight is then used to calculate the force required to pump the water out of the tank.

  • What is the weight density of water in US units?

    -In US units, the weight density of water is 62.5 pounds per cubic foot.

  • How is the volume of the tank described in the script?

    -The volume of the tank is described as being in the shape of a disc with a small thickness, where the radius is labeled as 'X' and the vertical distance or thickness as 'Dy'.

  • What geometric shape is the tank's cross-sectional area most similar to?

    -The tank's cross-sectional area is most similar to a circular disc, similar to the shape of a CD.

  • How does the script suggest finding the formula for the volume of a varying slice of the tank?

    -The script suggests using the formula for the area of a circle, \( \pi r^2 \), where 'r' is the radius, and then multiplying by the thickness 'Dy' to find the volume of each varying slice.

  • What is the method used to determine the value of 'X' (the radius) in terms of 'Y'?

    -The method used to determine the value of 'X' in terms of 'Y' is by finding the equation of the line that represents the side view of the tank, using the known points and the slope of the line.

  • What is the equation of the line used to find the relationship between 'X' and 'Y'?

    -The equation of the line used to find the relationship between 'X' and 'Y' is \( \frac{8}{3}x - y = 8 \), which is derived from the slope and the points given in the script.

  • How is the volume of the tank calculated after finding the relationship between 'X' and 'Y'?

    -The volume of the tank is calculated by integrating the formula for the volume of a disk, \( \pi (X)^2 \cdot Dy \), over the range of 'Y' from 0 to 8.

  • What is the significance of the distance '8 - y' in the calculation of work?

    -The distance '8 - y' represents the vertical distance each disk of water must travel to be pumped out of the tank, which is used in the calculation of work.

  • How is the work required to pump out the water calculated in the script?

    -The work required to pump out the water is calculated by integrating the product of the force (weight density times volume) and the distance '8 - y' over the range of 'Y' from 0 to 8.

Outlines
00:00
🧮 Calculating Work to Pump Water from a Tank

In this segment, we calculate the work needed to pump water out of a bucket-shaped tank. The work involves the force, which equates to the weight. To determine the weight, we consider the volume and then multiply by the density of water (62.5 pounds per cubic foot in US units). The hardest part is calculating the volume, done by slicing the tank horizontally and considering each slice as a thin circular disk. The radius of each disk changes depending on its vertical position, complicating the volume calculation. We then look at a front view of the tank to derive the formula for the radius in terms of vertical distance.

05:06
🔢 Deriving the Formula for Radius in Terms of Vertical Distance

Here, we derive a formula for the radius of the tank's horizontal slices in terms of the vertical distance (y). We start by identifying key points and measurements on the front view of the tank. The slope of the line representing the side of the tank is calculated and used to form an equation. Through algebraic manipulation, we isolate x (radius) as a function of y. We then use this formula in the volume calculation of the disks by integrating over the height of the tank.

Mindmap
Keywords
💡Work
In the context of physics, 'work' is defined as the product of the force applied to an object and the distance over which it is applied in the direction of the force. In the video, work is central to calculating the effort required to pump water out of a tank, using the formula 'force times distance'. The script discusses calculating work by considering the weight of the water, which is a force due to gravity, and the distance the water must be moved.
💡Force
Force is a push or pull upon an object resulting from its interaction with another object. In the script, the force required to pump water is primarily due to the weight of the water, which is a form of force acting vertically downwards due to gravity. The concept is integral to the work calculation and is directly related to the weight and distance the water is moved.
💡Weight
Weight is the force exerted on a body due to gravity. It is calculated by multiplying the mass of the object by the acceleration due to gravity. In the video, the weight of the water is determined by its volume and density, and it is a key factor in calculating the force needed to pump the water out of the tank.
💡Density
Density is a measure of mass per unit volume of a substance. It is crucial in the script for determining the weight of the water, as the density of water varies with units (e.g., pounds per cubic foot in US units). The script mentions the density of water as 62.5 pounds per cubic foot, which is used to calculate the weight and, subsequently, the work required.
💡Volume
Volume refers to the amount of space that a substance or object occupies. In the script, the volume of water in the tank is essential for calculating its weight and, by extension, the work needed to pump it out. The volume calculation involves considering the shape of the tank, described as cylindrical with a small thickness.
💡Cylinder
A cylinder is a three-dimensional shape with parallel and congruent circular bases connected by a curved surface. The script describes the tank as being in the shape of a cylinder with a circular base and a small vertical thickness, which is important for calculating the volume of water it contains.
💡Radius
The radius is the distance from the center of a circle to any point on its edge. In the context of the script, the radius (labeled as 'X') is used to describe the size of the circular base of the cylindrical tank, which is necessary for calculating the volume of the water.
💡Thickness
Thickness refers to the extent of something from one surface to another, especially in a direction perpendicular to the surfaces. In the script, the thickness (labeled as 'Dy') of the cylindrical tank is mentioned as an important dimension for calculating the volume of the water it holds.
💡Integration
Integration in mathematics is a method of summing the values of a function over an interval to find the total quantity. In the script, integration is used to calculate the total work required to pump out all the water from the tank by summing the work for each 'disc' of water from the bottom to the top of the tank.
💡Slope
Slope is a measure of the steepness of a line, defined as the ratio of the vertical change to the horizontal change between two points on the line. The script calculates the slope of a line to determine the relationship between the 'X' (radius) and 'Y' (height) coordinates, which is essential for deriving the formula for the radius in terms of height.
💡Equation of a Line
The equation of a line is a mathematical expression that defines the relationship between the coordinates of any point on the line. In the script, the equation of a line is derived to express the radius 'X' in terms of the height 'Y', which is necessary for calculating the volume of the cylindrical tank.
Highlights

Introduction to calculating the work required to pump water from a tank that resembles a bucket.

Explanation of the force times distance formula for calculating work.

Identification of weight as the primary force for the work calculation.

Clarification on the units used and the weight density of water in US units.

Approach to calculating the volume of the tank by considering its shape.

Labeling the dimensions of the tank for volume calculation: radius as X and thickness as Dy.

Understanding the varying thickness of the tank and its impact on volume calculation.

Derivation of a formula for the volume of a slice of the tank based on changing radius.

Use of the trapezoidal shape of the tank's front to derive the radius in terms of Y.

Calculation of the slope of the line representing the tank's front.

Isolation of X in terms of Y using algebraic manipulation.

Formulation of the volume equation for the tank as a function of Y.

Inclusion of the tank's density in the volume calculation.

Integration of the volume formula to account for the entire tank's volume.

Determination of the distance traveled by a disc of water during pumping.

Calculation of work by integrating the distance and volume of water discs.

Integration limits from the bottom to the top of the tank for complete work calculation.

Transcripts

Browse More Related Video

Calculating Work, pumping water out of a tank, calculus 2 tutorial, application of integration

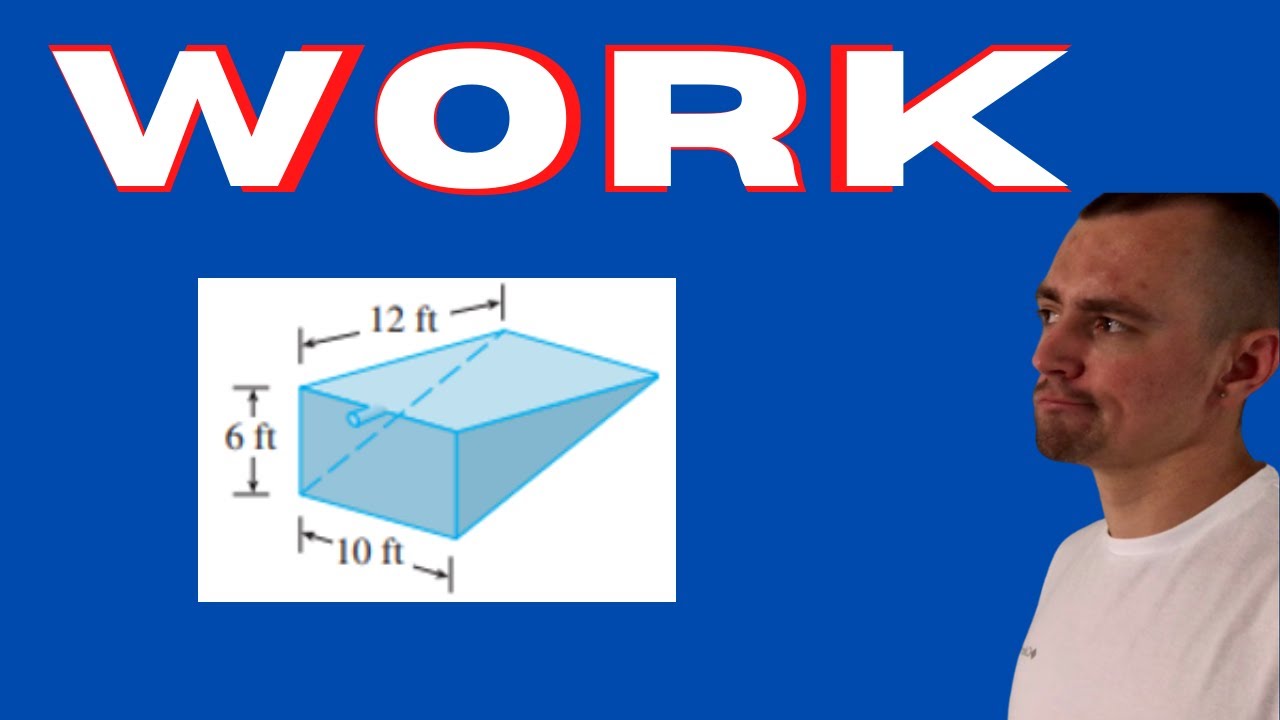
FIND THE WORK REQUIRED TO PUMP THE WATER OUT OF THE TANK

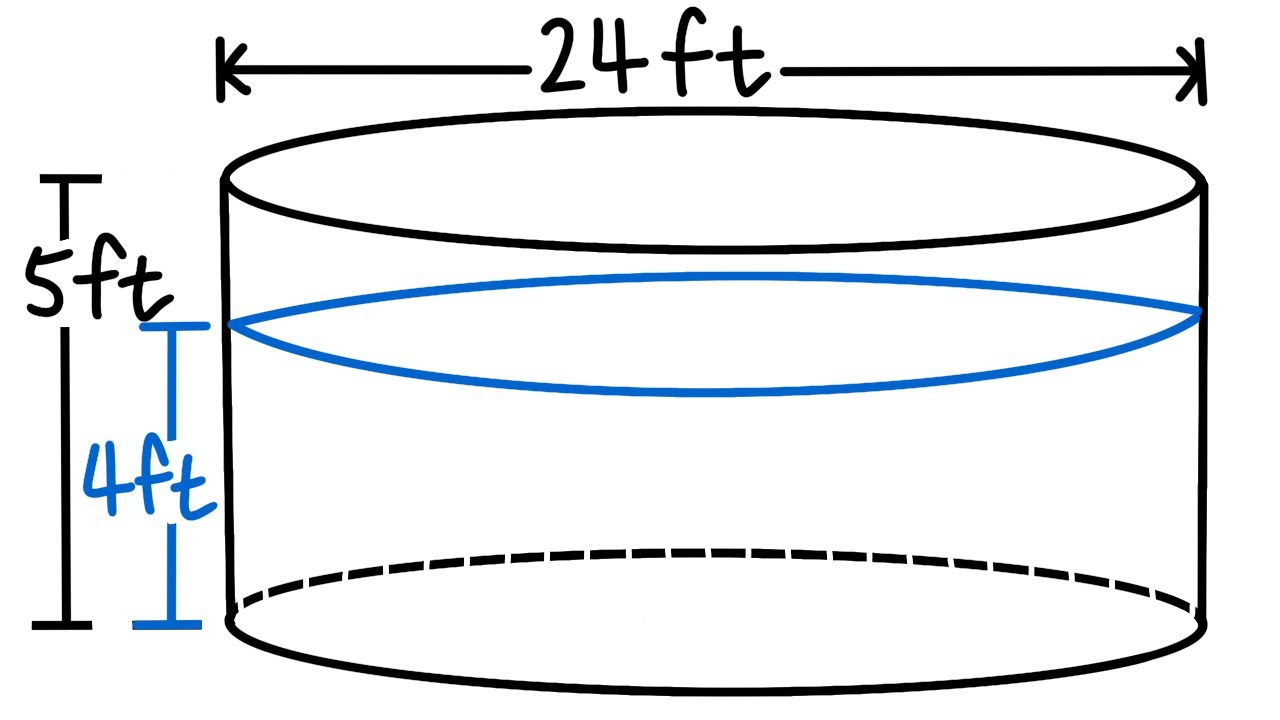
Calculating Work, pumping water out of a circular swimming pool

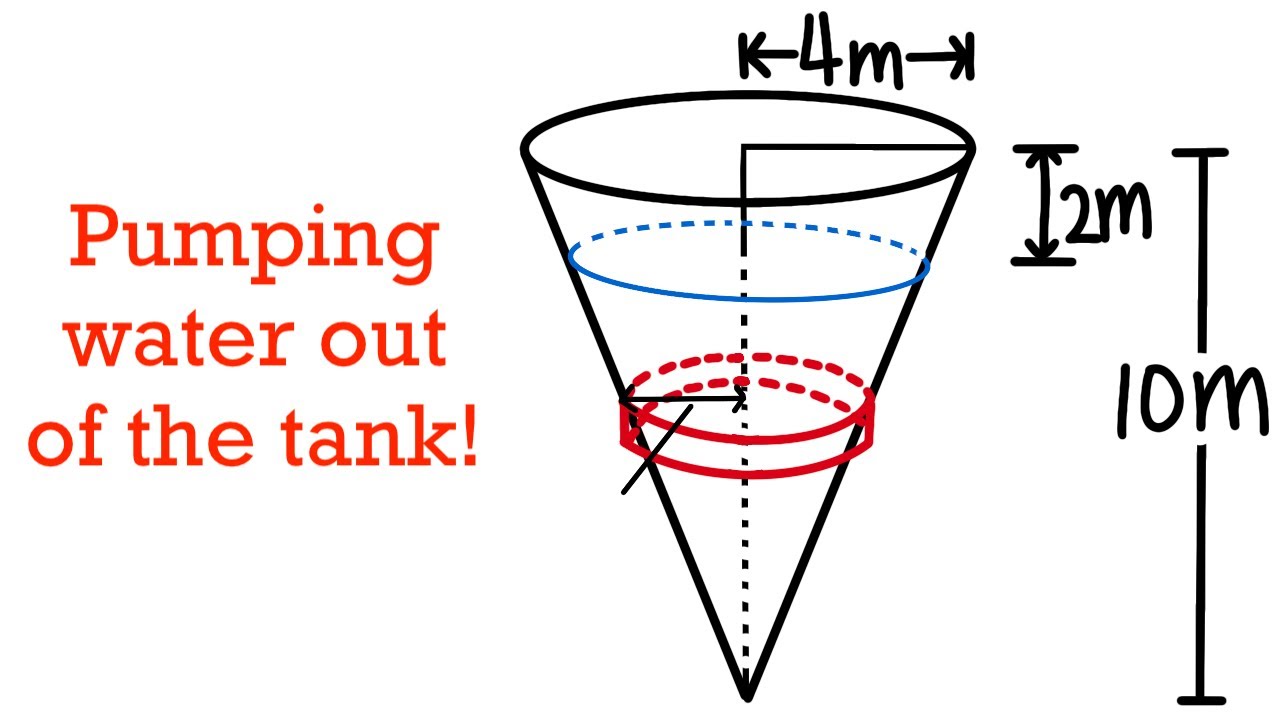
calculating work by using integral, pumping water out of a tank, calculus 2 tutorial

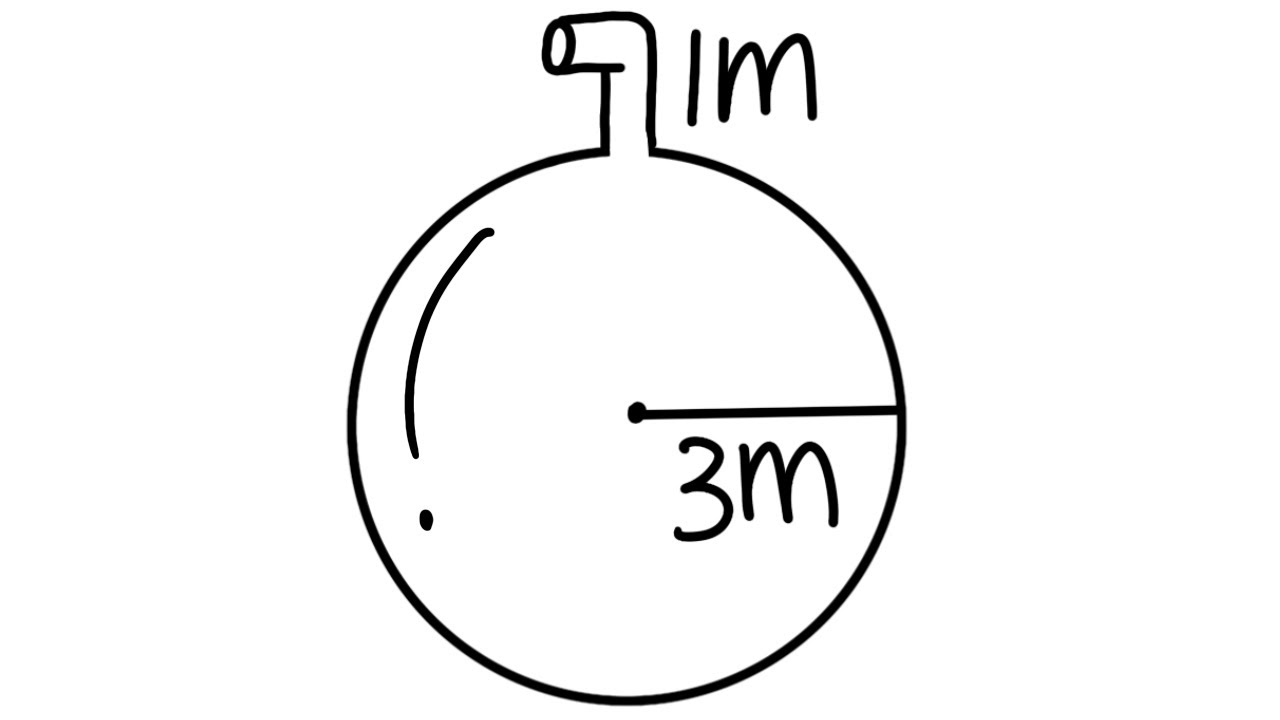
Pumping water out of a spherical tank, calculating work, calculus 2 tutorial

Calculate Work to Pump Liquid Out of Tanks - Calculus 2

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Water PumpingWork CalculationPhysicsForceVolumeDensityIntegrationMathEngineeringTank