calculating work by using integral, pumping water out of a tank, calculus 2 tutorial
TLDRThe video script delves into calculating the work required to pump water out of a tank to the top. It explains the concept of work as force times distance, emphasizing the importance of understanding density and volume in calculating weight. The script guides through setting up a reference frame, integrating geometry with algebra to find the volume of a cylinder, and using the mass density of water. It also covers the integration process to calculate the work needed, considering the distance water must be pumped and the tank's geometry, ultimately challenging viewers to solve the problem themselves.
Takeaways
- 🔍 The primary question is to calculate the work required to pump water from a tank to the top so it can be dispensed.
- 📚 Work is defined as force times distance, and force in this context is related to the weight of the water.
- 📏 Weight is calculated by considering both density and volume, with two types of density mentioned: weight density and mass density.
- 🌡 The units used for calculations are crucial, with SI units requiring a multiplication by 9.8 for gravity, whereas US units may already account for this in the density.
- 💧 The mass density of water is 1,000 kg/m³, which is a key constant in the calculations.
- 📐 The volume of the water in the tank is determined by geometrical methods, starting with a horizontal cut that creates a cylinder shape.
- 📉 The volume calculation involves integrating over the thickness of the cylinder, represented as dy, and the radius as a function of x.
- 📈 The density part of the work calculation requires multiplying by 9.8 for SI units to account for gravity.
- 📍 The distance for the work calculation is the vertical distance from the water level to the top of the tank, adjusted for the empty space at the top.
- ∫ The work is found by integrating the product of force, distance, and volume over the range of the water level from 0 to 8 meters.
- 📝 The relationship between x and y is established using the equation of a line derived from the geometry of the tank, which simplifies the integration process.
Q & A
What is the definition of work in the context of this script?
-In this script, work is defined as the product of force and distance, which is a fundamental principle in physics.
What are the two main factors to consider when calculating weight according to the script?
-The two main factors to consider when calculating weight are density and volume.
What is the difference between weight density and mass density mentioned in the script?
-Weight density refers to the force exerted by gravity on an object, while mass density is the mass per unit volume of the object. The script mentions the importance of distinguishing between the two when calculating weight.
Why is it important to pay attention to units when calculating weight in the SI unit system?
-In the SI unit system, it's important to multiply by 9.8 (the acceleration due to gravity) when calculating weight from mass density to ensure the units are consistent and correct.
What is the significance of the number 1,000 in the context of mass density of water?
-The number 1,000 represents the mass density of water in kilograms per cubic meter, which is a standard value used in calculations.
How does the script suggest finding the volume of a cylinder?
-The script suggests using the formula for the volume of a cylinder, which is the area of the base (pi times the radius squared) multiplied by the height.
What is the purpose of setting up a reference frame with x and y axes in the script?
-Setting up a reference frame with x and y axes helps in applying geometric and algebraic methods to calculate the volume and other necessary measurements for the problem.
How does the script describe the process of finding the work needed to pump water from a tank?
-The script describes the process as an integration over the volume elements of the water in the tank, considering the force of gravity, the density of water, and the vertical distance from each element to the top of the tank.
What is the equation of the line used in the script to relate x and y coordinates?
-The equation of the line is derived from the points (0,0) and (4,10), resulting in the slope of 5/2, and the equation y = (5/2)x.
How does the script calculate the work for pumping water out of the tank?
-The script calculates the work by integrating the product of the force (due to gravity and density), the volume of each thin disc of water, and the vertical distance from the disc to the top of the tank, from y=0 to y=8.
Outlines
🔍 Calculating Work to Pump Water: Understanding the Basics
The speaker is addressing a problem related to calculating the work required to pump water from a tank to its top. They start by defining work as force times distance and then delve into the concept of weight, which is crucial for this calculation. The speaker explains the importance of understanding density, both mass density and weight density, and how it relates to the volume of the water being pumped. They emphasize the need to pay attention to units, especially when using the SI system, where gravity (9.8 m/s²) must be considered. The speaker also introduces the concept of calculating the volume of a cylinder, which is part of the geometry needed to solve the problem, and sets up a reference frame to facilitate the calculation.
📚 Advanced Calculations for Pumping Water: Geometry and Integration
In this paragraph, the speaker continues the discussion on calculating the work needed to pump water, focusing on the vertical distance from the tank's bottom to its top. They explain how to determine the distance 'y' and how it relates to the overall work calculation. The speaker introduces the concept of integrating the work over the height of the tank, from 0 to 8 meters, to account for the varying distances water particles must travel. They also discuss the importance of the horizontal distance 'x' and how it can be derived from the geometry of the tank using algebra. The speaker provides a step-by-step guide on setting up the equation of a line to relate 'x' and 'y', and how to use this relationship in the work formula. The paragraph concludes with an integral expression that encapsulates the work calculation, inviting viewers to solve it as a challenge.
Mindmap
Keywords
💡Work
💡Force
💡Density
💡Volume
💡Weight
💡SI Units
💡Cylinder
💡Integrate
💡Geometry
💡Equation of a Line
💡Mass Density
Highlights
The video discusses calculating the work required to pump water from a tank to its top.
Work is defined as force times distance, emphasizing the importance of understanding these fundamental concepts.
Force is equated to weight, which is calculated based on density and volume.
Differentiating between weight density and mass density, especially in the context of units and their impact on calculations.
The importance of using the correct units, particularly SI units, and the necessity to multiply by gravity (9.8) in such cases.
The concept of 'magic number' 1,000 for the mass density of water in certain units, emphasizing precision in measurements.
Setting up a reference frame for geometrical and algebraic calculations to determine the volume of the water.
Using the formula for the volume of a cylinder to approach the problem of finding the volume of water in the tank.
Integrating calculus to find the volume by considering the tank as a series of infinitesimally thin cylinders.
The process of finding the density of water, highlighting the constants involved and the need for unit consistency.
Calculating the work by integrating the force over the distance, from the bottom to the top of the tank.
The significance of the vertical distance (Y value) in calculating the work needed to pump water out.
Integrating from a specific range (0 to 8) to account for the empty space at the top of the tank.
The use of geometry and algebra to find the relationship between X and Y coordinates in the tank.
Deriving the equation of the line that represents the tank's shape and its implications for the calculations.
Isolating X to find its relationship with Y, which is crucial for the integral calculation of work.
The final integral setup to calculate the work, incorporating all the derived variables and constants.
Encouraging viewers to perform the calculations themselves and to engage by commenting with their findings.
Transcripts
Browse More Related Video
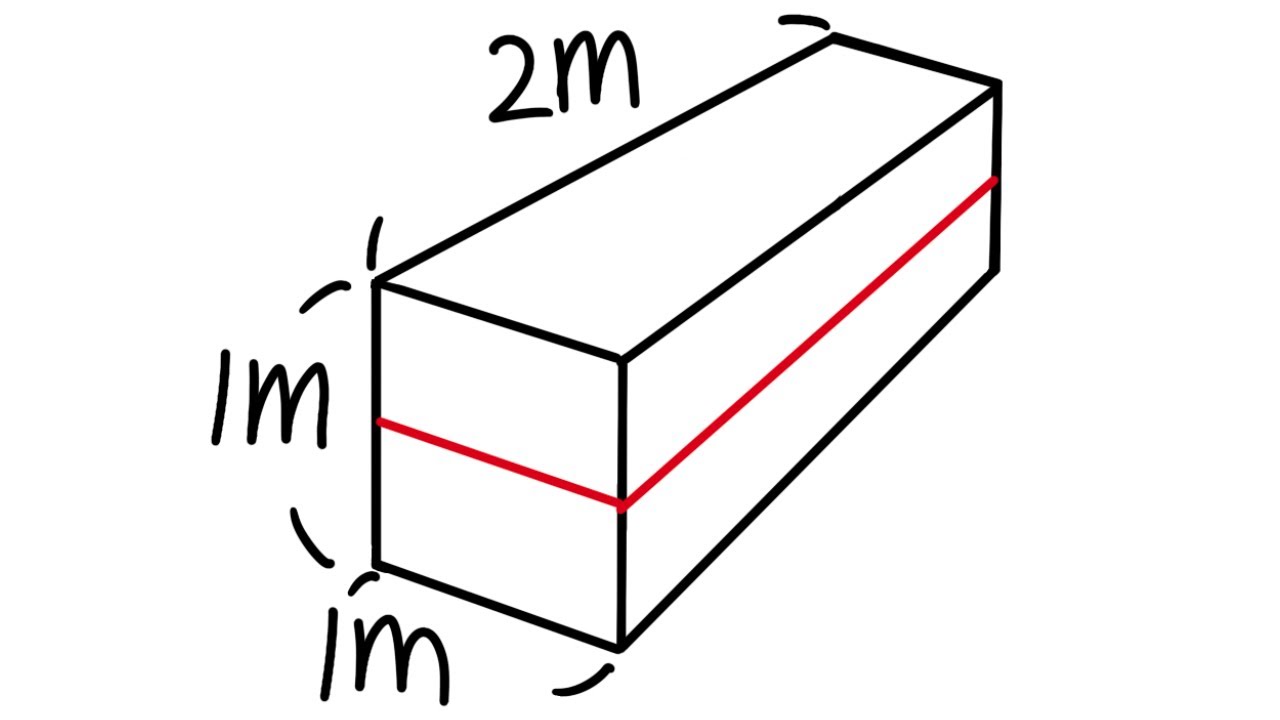
calculating work, pumping water out of a rectangular tank, calculus 2 tutorial

Calculating Work, pumping water out of a tank, calculus 2 tutorial, application of integration
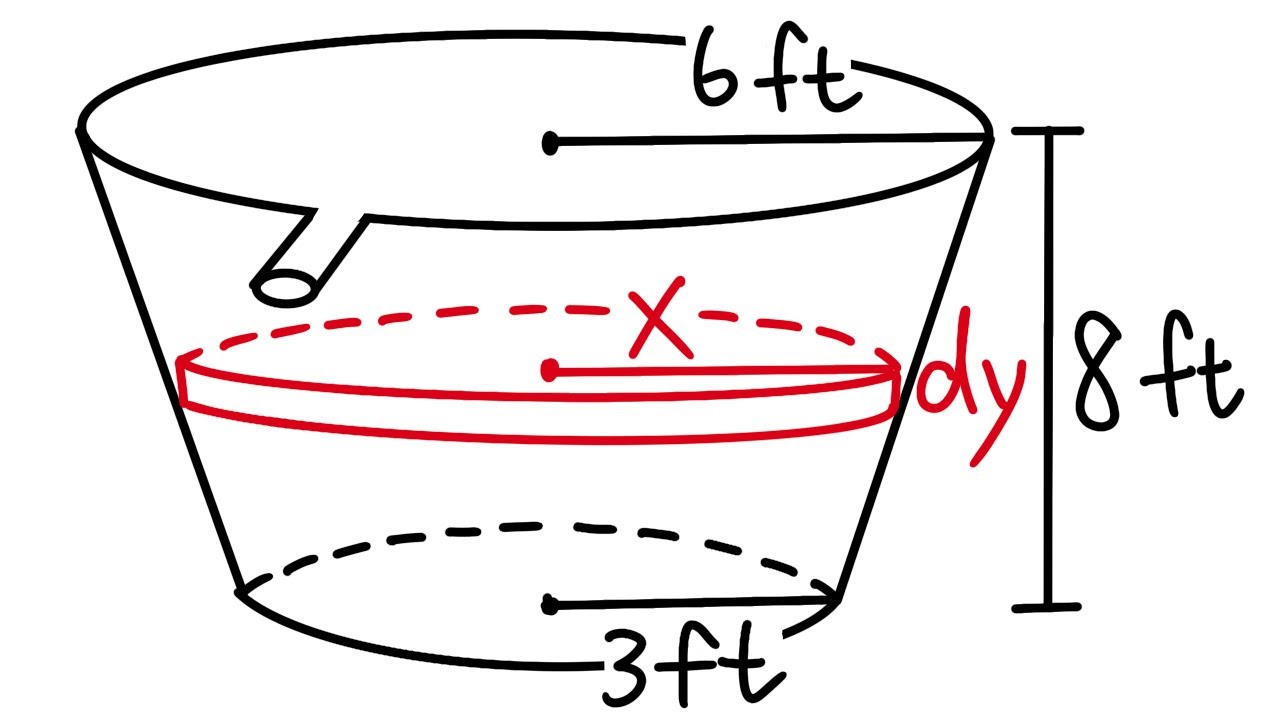
Pumping water out of a bucket, calculating work, calculus 2 tutorial
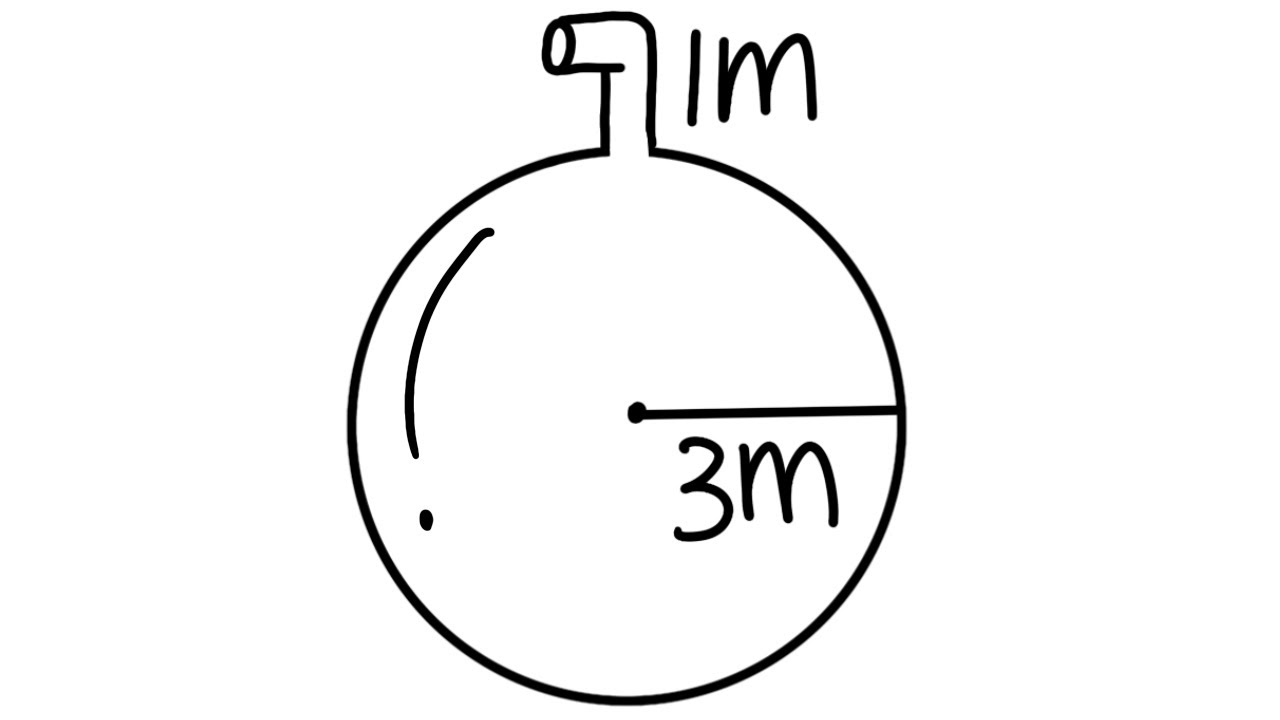
Pumping water out of a spherical tank, calculating work, calculus 2 tutorial

Calculate Work to Pump Water Out of Rectangular Tank
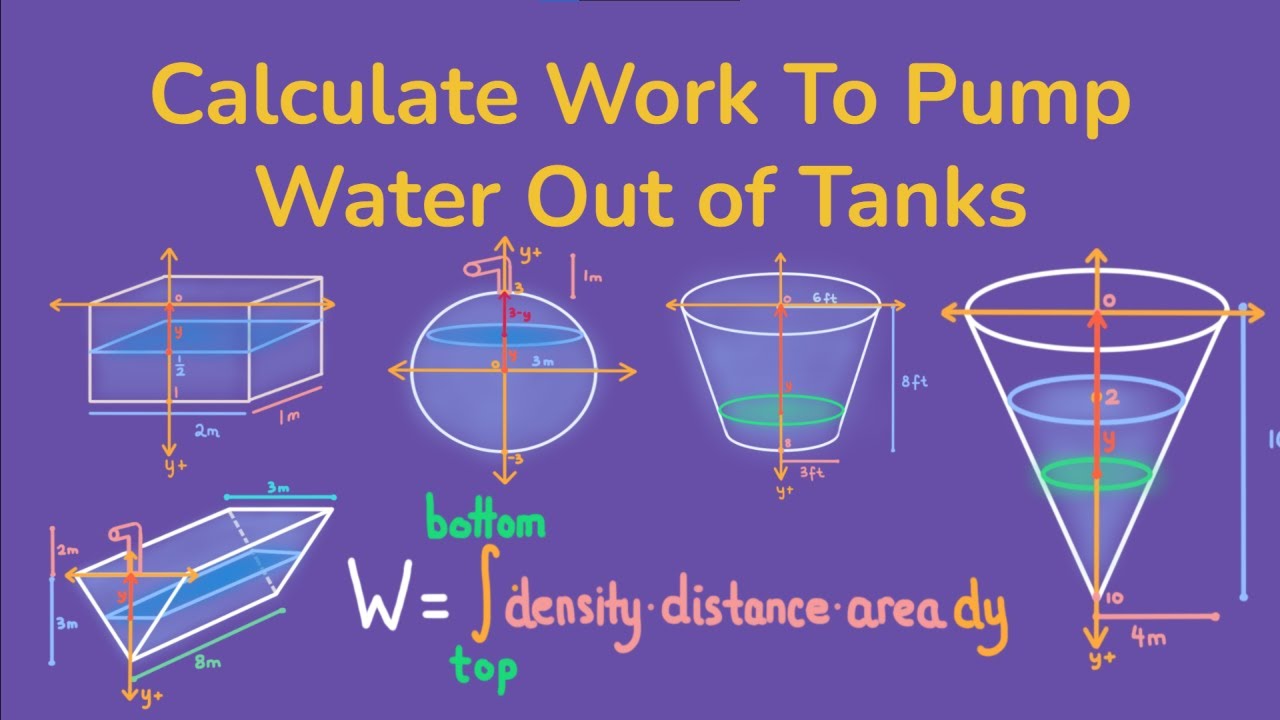
Calculate Work to Pump Liquid Out of Tanks - Calculus 2
5.0 / 5 (0 votes)
Thanks for rating: