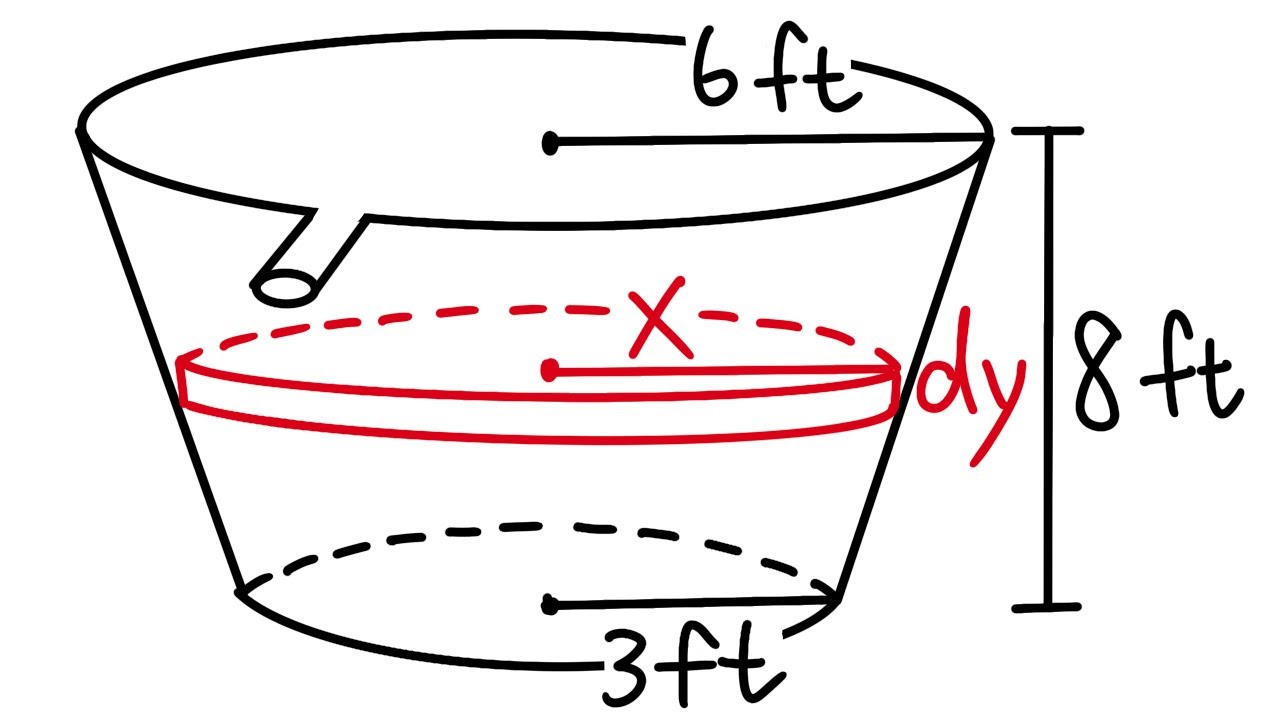
A tank is full of water. find the work required to pump

WNY Tutor
30 Oct 201608:25
EducationalLearning
32 Likes 10 Comments

TLDRThe video script presents a detailed physics problem involving the calculation of work done to lift water from a cylindrical tank through a spout. It introduces a small cylindrical portion of water with variable thickness Delta X and radius R, which is expressed in terms of the depth X below the spout. Using geometric similarity and the volume formula for a cylinder, the script derives an expression for the force required to lift this portion. The work done on the entire tank of water is then calculated through integration, resulting in a final answer of approximately 1.04 * 10^5 foot-pounds, illustrating the application of calculus in physics.

Takeaways
  • 📏 The problem involves measuring the depth 'x' below the spout at the top of a water tank.
  • 📐 The entire height of the tank is 8 feet, and the distance from the top to the water surface is '8 - x'.
  • 🔍 A small cylindrical portion of water is considered for calculating the volume and force required to lift it.
  • 📏 The thickness of the cylindrical portion is denoted as 'Delta X', a very small quantity.
  • 🌀 The volume of the cylindrical portion is calculated using the formula for the volume of a cylinder: Pi * radius^2 * height.
  • 📐 The radius 'r' of the cylinder is derived from the geometry of the tank, involving similar triangles and proportions.
  • 🔢 The expression for the radius 'r' in terms of 'x' is derived using the tank's dimensions and the concept of similar triangles.
  • ⚖️ The force required to lift the water is the weight of the water, calculated as the density times the volume.
  • 🔄 The work done to lift the water is the force times the distance, which is the depth 'x' below the spout.
  • ∫ The total work done on all the water in the tank is found by integrating the work function from 0 to 8 feet.
  • 📊 The final answer for the work done is obtained by evaluating the integral and is approximately 1.04 * 10^5 foot-pounds.
Q & A

  • What is the purpose of the video script?

    -The purpose of the video script is to explain the process of calculating the work required to empty a tank of water through a spout by integrating the work done on small cylindrical portions of water.

  • What is the significance of the variable 'x' in the script?

    -In the script, 'x' represents the depth below the spout at the top of the tank, which is used to calculate the distance the water must travel to be lifted out through the spout.

  • What is the total height of the tank mentioned in the script?

    -The total height of the tank is 8 feet, as indicated in the script.

  • What is the role of the small cylindrical portion of water in the script?

    -The small cylindrical portion of water is used to represent an infinitesimally small part of the water in the tank, which helps in applying the concept of integration to calculate the total work done.

  • What is the significance of the term 'Delta X' in the script?

    -The term 'Delta X' is used to denote the very small thickness of the cylindrical portion of water being considered for the calculation of work done on that portion.

  • How is the radius of the cylinder related to the variable 'x' in the script?

    -The radius of the cylinder is expressed in terms of 'x' using the derived expression involving similar triangles and the proportions of the tank's dimensions.

  • What is the density of the water given in the script?

    -The density of the water is given as 62.5 pounds per cubic foot.

  • How is the force required to lift a small portion of water calculated in the script?

    -The force required to lift a small portion of water is calculated by multiplying the density of the water by the volume of that portion.

  • What is the formula for the work done on a small portion of water in the script?

    -The work done on a small portion of water is the product of the force acting on that portion and the distance it has to travel, which is represented by the variable 'x'.

  • What mathematical concept is used to calculate the total work done on all the water in the tank?

    -The mathematical concept of integration is used to calculate the total work done on all the water in the tank by summing up the work done on infinitesimally small portions of water.

  • What is the final result of the calculation in the script?

    -The final result of the calculation is approximately 1.04 * 10^5 foot-pounds, representing the total work required to empty the tank.

Outlines
00:00
📏 Measuring Depth and Calculating Water Volume

The video script begins by instructing viewers to pause and attempt a problem on their own before continuing. The problem involves measuring the depth below the spout at the top of a tank, using the variable 'x' to represent the distance between two arrowheads on a diagram. The tank's total height is given as 8 feet, allowing the calculation of the remaining distance as '8 - x'. A small cylindrical portion of water within the tank is highlighted, with a thickness denoted by 'Delta X'. The volume of this cylinder is calculated using the formula for the volume of a cylinder, which is π times the radius squared times the height. The script then introduces a diagram with a circle representing the cylinder and labels various distances, including 'D', which is derived from the relationship between similar triangles in the diagram. The radius 'r' of the cylinder is expressed in terms of 'x', and this expression is used to calculate the volume of the water. The force required to lift the water is determined by multiplying the water's density by its volume.

05:02
🔄 Calculating Work Done on Water through Integration

The second paragraph delves into the concept of work done on the water within the tank. It starts by defining work as the force acting on a cylindrical portion of water times the distance it must travel, which is represented by 'x'. The work done on this small portion is then simplified by moving 'x' to the front of the equation. The script introduces the idea of integrating this work function across the entire height of the water, from 0 to 8 feet, to find the total work done on all the water. The integration process involves removing constants and changing the notation from 'Delta X' to 'DX'. The script guides through the integration process, which includes expanding the expression, simplifying, and then integrating term by term. The limits of integration are applied, and the result is simplified to find the total work done, which is given in foot-pounds. The final step involves plugging the upper limit of integration into the integrated function and subtracting the result of the lower limit, which simplifies to zero due to the nature of the function. The final answer is calculated to be approximately 1.04 * 10^5 foot-pounds, representing the work done to lift all the water out through the spigot.

Mindmap
Keywords
💡Cylinder
A cylinder is a three-dimensional geometric shape with parallel and congruent circular bases connected by a curved surface. In the video, the concept of a cylinder is central to understanding the volume of water in the tank, which is approximated by considering a series of infinitesimally thin cylindrical portions. The script uses the formula for the volume of a cylinder, \( \pi r^2 h \), where \( r \) is the radius and \( h \) is the height, to calculate the volume of these portions.
💡Volume
Volume refers to the amount of space occupied by a substance or object. In the context of the video, the volume is used to calculate the space taken up by the water in the tank, which is essential for determining the work required to lift the water out through the spout. The script describes how to calculate the volume of a cylindrical portion of water using the formula for the volume of a cylinder.
💡Density
Density is a measure of mass per unit volume of a substance. In the script, the density of water is given as 62.5, which is used to calculate the weight of the water in the tank. The weight is then used to determine the force required to lift a small cylindrical portion of water, which is a key step in calculating the work done.
💡Force
Force is a push or pull upon an object resulting from its interaction with another object. In the video, the force is calculated by multiplying the density of the water by its volume, which represents the weight of the water. This force is then used to determine the work done on a small cylindrical portion of water as it is lifted.
💡Work
Work in physics is defined as the product of the force acting on an object and the distance over which it is applied. The script explains how to calculate the work done on the water in the tank by multiplying the force (weight of the water) by the distance the water must be lifted, which is represented by the variable \( X \) in the script.
💡Integration
Integration is a fundamental concept in calculus that represents the process of summing up infinitesimally small quantities to find a total. In the script, integration is used to calculate the total work done on all the water in the tank by summing up the work done on each infinitesimally small cylindrical portion of water from the bottom to the top of the tank.
💡Similar Triangles
Similar triangles are triangles that have the same shape but different sizes, with corresponding angles being equal and corresponding sides being in proportion. The script identifies two similar triangles in the diagram of the tank and uses their proportionality to derive an expression for the radius of the cylindrical portion of water in terms of the variable \( X \).
💡Proportion
A proportion is a statement that two ratios are equal. In the context of the video, the script uses the concept of proportion to relate the sides of similar triangles, allowing for the calculation of the radius of the cylinder based on the known dimensions of the tank and the depth \( X \) below the spout.
💡Radius
The radius is the distance from the center of a circle to any point on its edge. In the script, the radius of the cylindrical portion of water is calculated using the derived expression involving the tank's dimensions and the variable \( X \). This radius is crucial for calculating the volume of the cylinder and, subsequently, the work done on the water.
💡Integral
An integral in calculus is a mathematical operation that represents the process of integration. The script describes the process of integrating the work function over the distance that the water must travel, from 0 to 8 feet, to find the total work done on the water in the tank.
💡Foot-pound
A foot-pound is a unit of measurement for work in the Imperial system, where work is calculated as the product of force in pounds and distance in feet. The script concludes with the calculation of work in foot-pounds, which is the result of multiplying the force (in pounds) by the distance (in feet) the water is lifted.
Highlights

The problem involves calculating the work done to lift water out of a tank through a spigot.

The depth below the spout is measured by variable X.

The total height of the tank is given as 8 feet.

A small cylindrical portion of water is considered for calculation, with thickness Delta X.

The volume of the cylindrical water portion is calculated using the formula for a cylinder.

The radius of the cylinder is derived from the geometry of the tank.

Similar triangles are identified to express the radius in terms of X.

An expression for the radius R in terms of X is developed using proportions.

The force required to lift the water is calculated as the weight of the water.

The density of water is given as 62.5, used in the force calculation.

The work done on a small portion of water is the force times the distance X.

Integration is used to calculate the total work done on all the water in the tank.

The integral of the work function is simplified by moving constants outside the integral.

The integral is solved by applying the power rule and distributing terms.

The upper limit of integration is 8 feet, representing the full height of the tank.

The lower limit of integration is 0, which simplifies the calculation.

The final result of the integral gives the total work done in foot-pounds.

The approximate numerical value of the work done is calculated.

Transcripts

Browse More Related Video

Pumping water out of a spherical tank, calculating work, calculus 2 tutorial

Calculus gr 12 Exam Questions

Calculating Work, pumping water out of a circular swimming pool

Work Done Raising a Leaky Bucket with an Integral

Pumping water out of a bucket, calculating work, calculus 2 tutorial

Calculus Work Pump Water From a Circular Swimming Pool

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsCalculusWork CalculationFluid DynamicsIntegrationCylinder VolumeForce AnalysisWater TankProblem SolvingEducational Content