Arc Length of Parametric Curves
TLDRThis educational video script offers a detailed guide on calculating the arc length of a parametric function. It explains the prerequisites for the formula's application, such as the continuity of derivatives and the curve's single traversal. The script walks through two examples, illustrating the process of finding derivatives, setting up integrals, and applying u-substitution to solve for arc lengths. It concludes with the final results, providing a clear understanding of the concept.
Takeaways
- 📚 The video explains how to calculate the arc length of a parametric function where x and y are functions of t, with conditions that f'(t) and g'(t) are continuous on the interval [α, β] and the curve is transverse once as t increases.
- 🔍 The formula for arc length is given by the integral from α to β of the square root of (dx/dt)^2 + (dy/dt)^2 with respect to t.
- 📘 The first example involves x(t) = 2 + 6t^2 and y(t) = 5 + 4t^3, with t ranging from 0 to √8, and the process of finding dx/dt and dy/dt is demonstrated.
- 🧩 The arc length calculation involves simplifying the integral and factoring out common terms to make the integration easier.
- 🔑 U-substitution is recommended as an integration technique, which is applied by setting u = 1 + t^2 and solving for dt in terms of du.
- 📉 The limits of integration change with the substitution, and the example shows how to evaluate these new limits based on the original variable t.
- ✂️ The integral is simplified by separating it into two radical expressions and integrating each part separately.
- 📈 The power rule for integration is used to find the antiderivative of the simplified expression, resulting in the arc length calculation.
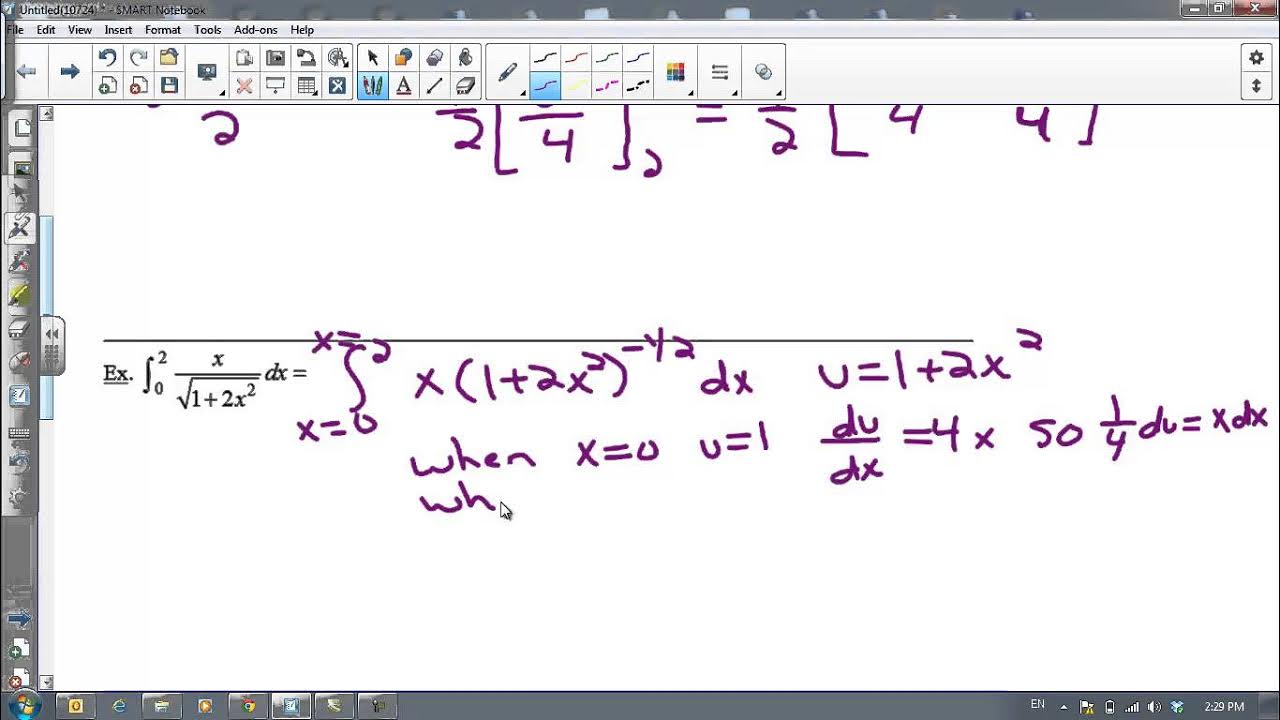
- 📝 The second example provided involves x(t) = 9t^2 and y(t) = 9t - 3t^3, with the goal of finding the arc length from 0 to 2.
- 📐 The process of simplifying the expression for the integral in the second example involves factoring and recognizing perfect square trinomials.
- 📊 The antiderivative for the second example is found by integrating t^2 and 1 separately, and then evaluating from the lower to the upper limit of integration.
- 🎯 The final step in both examples is to plug in the limits of integration to find the numerical value of the arc length.
Q & A
What is the formula for calculating the arc length of a parametric function?
-The arc length of a parametric function is calculated using the integral from alpha to beta of the square root of (dx/dt)^2 plus (dy/dt)^2 with respect to t, where x and y are functions of t, and f'(t) and g'(t) are continuous on the interval [alpha, beta].
What are the conditions required for the parametric curve to be considered for arc length calculation?
-The conditions are that x and y are functions of t, their derivatives f'(t) and g'(t) are continuous on the interval [alpha, beta], and the curve can only be traversed once as t increases.
In the example given, what are the functions for x and y in terms of t?
-In the example, x(t) = 2 + 6t^2 and y(t) = 5 + 4t^3.
What is the range of t for the first example problem in the script?
-The range of t for the first example is from 0 to the square root of 8.
How do you find dx/dt and dy/dt for the first example?
-For the first example, dx/dt is 12t (the derivative of 2 + 6t^2 with respect to t), and dy/dt is 12t^2 (the derivative of 5 + 4t^3 with respect to t).
What substitution method is recommended for evaluating the integral of the arc length formula in the first example?
-The recommended substitution method is u-substitution, where u = 1 + t^2, and then solving for dt in terms of du.
What is the integral expression for the arc length in the first example after simplification?
-After simplification, the integral expression for the arc length in the first example is the integral from 0 to the square root of 8 of 12t times the square root of (1 + t^2) with respect to t.
What is the antiderivative of the simplified arc length integral in the first example?
-The antiderivative involves integrating 12t * sqrt(1 + t^2), which after substitution becomes 6 times the integral from 1 to 9 of sqrt(u) du, leading to 4 * (u^(3/2)) evaluated from 1 to 9.
What is the final calculated arc length for the first example as t increases from 0 to the square root of 8?
-The final calculated arc length for the first example is 104 units.
What are the functions for x and y in the second example problem presented in the script?
-In the second example, x(t) = 9t^2 and y(t) = 9t - 3t^3.
How do you find the arc length for the second example where t ranges from 0 to 2?
-For the second example, you would calculate the integral from 0 to 2 of the square root of (18t)^2 plus (9 - 9t^2)^2 with respect to t, simplify the expression, and then integrate to find the arc length.
Outlines
📚 Finding Arc Length of Parametric Functions
This paragraph introduces the concept of finding the arc length of a parametric curve where both x and y are functions of a parameter t. It sets the conditions for the problem: the derivatives of x and y with respect to t must be continuous on the interval [α, β], and the curve should be traversed only once as t increases. The formula for arc length is given as the integral from α to β of the square root of (dx/dt)^2 + (dy/dt)^2. An example is provided with x(t) = 2 + 6t^2 and y(t) = 5 + 4t^3, with t ranging from 0 to √8. The process involves calculating dx/dt and dy/dt, simplifying the integral, and using u-substitution to evaluate it. The integral is simplified to √(144t^2 + t^4), factored, and then separated into two radical expressions, leading to the use of u-substitution with u = 1 + t^2 to find the arc length.
📈 Calculating Arc Length with U-Substitution
The second paragraph continues the example problem from the first, focusing on the application of u-substitution to evaluate the integral for arc length. It details the steps of changing the variable t to u, where u = 1 + t^2, and adjusting the differential dt to du/2t. The integral simplifies to 6 times the integral from 1 to 9 of the square root of u, which is then solved using the power rule for integration. The limits of integration are adjusted according to the values of t at the endpoints, resulting in the calculation of (9^(3/2) - 1^(3/2)) times 4, which simplifies to 104. This is the arc length as t increases from 0 to √8.
🔍 Advanced Arc Length Calculation with Factoring
The final paragraph presents a new example of calculating arc length with a different set of parametric equations: x(t) = 9t^2 and y(t) = 9t - 3t^3. The process involves finding dx/dt and dy/dt, and then applying the arc length formula. The integral to be solved is ∫√(18t^2 + (9 - 9t^2)^2) dt from 0 to 2. The expression is simplified by factoring and recognizing a perfect square trinomial, which allows the integral to be separated into two radicals. The resulting integral is 9 times the integral from 0 to 2 of (t^2 + 1) dt, which is then solved by finding the antiderivative and evaluating it at the endpoints, yielding a final arc length of 42.
Mindmap
Keywords
💡Arc Length
💡Parametric Function
💡Derivative
💡Integral
💡Square Root
💡Transverse
💡Continuous
💡U Substitution
💡Power Rule
💡Limits of Integration
💡Factor Out
Highlights
Introduction to the concept of finding the arc length of a parametric function.
Explanation of the conditions required for finding arc length, including the continuity of derivatives and the curve's transversality.
The mathematical formula for calculating arc length using the integral of the square root of the sum of squares of derivatives.
Example problem setup with parametric functions x(t) and y(t), and the restriction of t between 0 and √8.
Derivation of dx/dt and dy/dt for the given parametric functions.
Simplification of the integral expression for arc length by combining like terms and factoring out common factors.
Introduction of the u-substitution technique for integrating the simplified arc length expression.
Calculation of the new integral limits after applying u-substitution based on the original t limits.
Integration of the new expression using the power rule and simplification to find the arc length.
Final calculation of the arc length for the first example, resulting in a numerical answer.
Introduction of a second example problem with different parametric functions for x(t) and y(t).
Derivation of the new derivatives dx/dt and dy/dt for the second example.
Simplification of the integral for the second example by factoring and combining terms under a square root.
Identification of a perfect square trinomial in the integral expression and its factorization.
Integration of the factored expression to find the arc length for the second example.
Final calculation of the arc length for the second example, providing a step-by-step solution.
Conclusion of the video with the final arc length result for the second example.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: