Work Problems Examples | Calculus 2 - JK Math
TLDRThis video script explores various work problems solvable with calculus, starting with basic constant force scenarios like lifting a bag of cat litter and pushing a truck. It then transitions to variable force problems involving springs, where calculus is essential. The script explains calculating spring constants, work done in stretching springs, and introduces propulsion and lifting problems with variable forces, such as lifting a sandbag that loses weight. It concludes with pumping problems, calculating the work to pump water out of cylindrical and trough-shaped tanks, using integral calculus to find the total work done.
Takeaways
- 📚 The script provides an educational overview of work problems solvable with calculus, including both basic and advanced scenarios.
- 🔧 The fundamental concept of work is introduced as the energy transferred by a force along a displacement, calculated as force times displacement.
- 🚀 The first example demonstrates calculating the work done in lifting a 35-pound bag of cat litter to a height of 10 feet, resulting in 350 foot-pounds of work.
- 🚛 The second example illustrates the work done in pushing a truck 20 meters with a constant force of 300 newtons, equating to 6000 joules of work.
- 🔄 The script transitions to variable force problems, necessitating the use of calculus and definite integrals to calculate work, starting with spring problems.
- 🌱 An example of a spring problem is dissected, involving finding the spring constant, determining how far a 50-pound object would stretch the spring, and calculating work to stretch it to a specific length.
- 🔗 The spring constant is determined to be 20 pounds per foot using Hooke's Law, and the work required to stretch the spring to 4 feet is calculated to be 10 foot-pounds.
- ⚙️ Propulsion problems are discussed, involving lifting an object against gravity, with an example of lifting an astronaut 20 miles from the moon's surface.
- 🌌 The work done in a propulsion problem is calculated using Newton's law of universal gravitation, with the force varying inversely with the square of the distance from the center of mass.
- 🏗️ The script covers lifting problems with variable forces, such as a bag of sand losing weight as it is lifted, using a definite integral to calculate the work done.
- 💧 Pumping problems are introduced, where the work required to pump water out of a tank or trough is calculated using the weight density of the liquid and the volume of the liquid being moved.
Q & A
What is the basic formula for calculating work in the context of the video?
-The basic formula for calculating work is work equals force times displacement.
How many foot-pounds of work is required to lift a 35-pound bag of cat litter to a height of 10 feet?
-350 foot-pounds of work are required to lift a 35-pound bag of cat litter to a height of 10 feet.
What is the unit of work in the metric system?
-The unit of work in the metric system is the joule, which is equivalent to a newton meter.
How can you find the spring constant for a spring?
-You can find the spring constant by using Hooke's Law, which states that the force on the spring is equal to the spring constant times the displacement of the spring.
What is the spring constant in pounds per foot for a spring that stretches 0.5 feet under a 10-pound force?
-The spring constant is 20 pounds per foot, calculated by dividing the force (10 pounds) by the displacement (0.5 feet).
How much work is required to stretch a spring from its natural length to a length of 4 feet, given a spring constant of 20 pounds per foot?
-The work required is 10 foot-pounds, calculated by integrating the force function (20x) from the spring constant over the displacement (from 0 to 1 foot).
What is the formula for calculating work when dealing with a variable force?
-The formula for calculating work with a variable force is the integral from a to b of the force function times dx.
How much work is needed to stretch a spring one foot beyond its natural length if it requires 15 foot-pounds to stretch it eight inches?
-The work needed is 30 foot-pounds, derived from the integral of the spring force function (30x) over the displacement (from 0 to 1 foot), after converting 8 inches to feet.
What is the force exerted by gravity on an astronaut weighing 180 pounds on Earth's surface on the surface of the Moon?
-The force exerted by gravity on the Moon's surface is 30 pounds, which is 1/6th of the astronaut's weight on Earth.
How can you calculate the work done in lifting an object with a variable force, such as a bag of sand that loses weight as it is lifted?
-You can calculate the work done by setting up a definite integral with the variable force function, which represents the changing weight of the object, and integrating over the displacement.
What is the work done in lifting a bag of sand 18 feet high if it starts at 144 pounds and loses half its weight during the lift?
-The work done is 1944 foot-pounds, calculated by integrating the force function (144 - 4x) from 0 to 18 feet.
How do you calculate the work required to wind a rope onto a pulley when lifting a bucket?
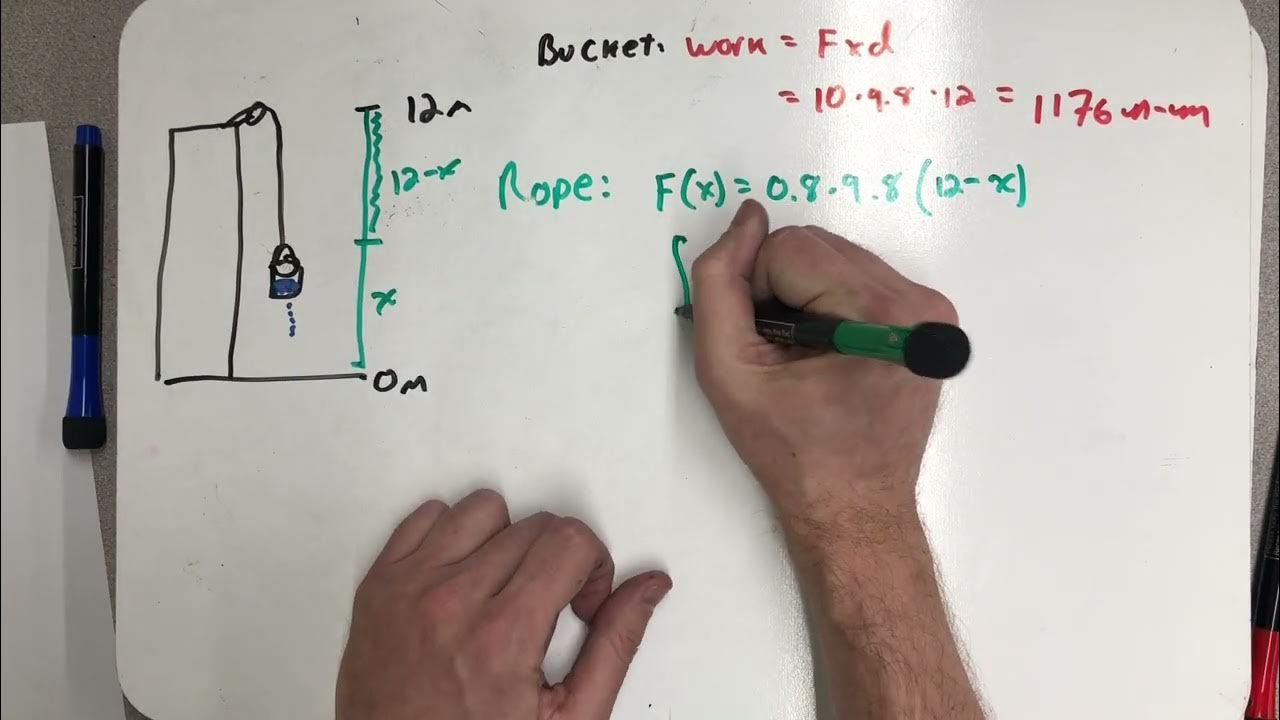
-The work required is calculated using the formula for work with a variable force, integrating the force function that accounts for the bucket's weight and the decreasing weight of the rope as it is wound onto the pulley.
What is the work done in winding a 30-foot rope onto a pulley to lift a 15-pound bucket?
-The work done is 675 foot-pounds, calculated by integrating the force function (30 - 0.5x) from 0 to 30 feet.
How can you find the work required to pump all the water out of a cylindrical tank?
-The work required is found by integrating the product of the weight density of the liquid, the cross-sectional area of the water slice, the displacement, and dx over the height of the water in the tank.
What is the work done by pumping water out of a tank that is two-thirds filled with water up to a height of 6 feet?
-The work done is calculated by integrating the force on slices of water over the height of the water, resulting in approximately 56,160π foot-pounds.
How do you calculate the work required to pump water over the top of a trough with triangular ends?
-The work is calculated using the weight density of water and integrating the cross-sectional area of the water slice (20x) times the displacement (3 - x) over the height of the water (from 0 to 1 foot).
What is the work required to pump all the water over the top of a trough filled to a height of 1 foot?
-The work required is 1456 foot-pounds, obtained by evaluating the integral of the work formula over the height of the water in the trough.
Outlines
📚 Introduction to Work Problems in Calculus
The video begins with an introduction to work problems that can be solved using calculus. It starts with two basic examples involving constant forces: lifting a 35-pound bag of cat litter to a height of 10 feet and pushing a truck 20 meters with a force of 300 newtons. The work done in these scenarios is calculated using the formula work = force × displacement. The video then transitions to more complex problems involving variable forces, which will be addressed using calculus, specifically definite integrals.
🔍 Calculating Spring Constant and Work Done
This paragraph delves into spring problems, where the work done in stretching or compressing a spring is calculated. The example given involves a spring with a natural length of 3 feet, stretched to 3.5 feet by a 10-pound weight. The spring constant is determined to be 20 pounds per foot. Further, it explains how to calculate the displacement and work required to stretch the spring to different lengths, eventually using calculus to find the work needed to stretch the spring to 4 feet, which is found to be 10 foot-pounds.
🚀 Propulsion Problems and Calculating Work in Space
The script moves on to propulsion problems, which involve lifting objects into space. An example is provided where an astronaut, weighing 180 pounds on Earth, needs to be lifted 20 miles from the Moon's surface. The Moon's gravity is 1/6th of Earth's. The work done in this scenario is calculated using a force function derived from Newton's law of universal gravitation. The constant of proportionality is determined, and a definite integral is used to calculate the work, which is approximately 3,111,428.6 foot-pounds.
🏗️ Lifting Problems with Variable Forces
The paragraph discusses lifting problems where the force is variable, such as a bag of sand that loses sand at a constant rate as it is lifted. The bag initially weighs 144 pounds and is lifted to a height of 18 feet, at which point it weighs half of its original weight. The work done in lifting the sand is calculated using a definite integral with a force function that accounts for the decreasing weight of the sand. The final work required is found to be 1944 foot-pounds.
🪣 Winding a Rope and the Work Done in Lifting a Bucket
This section describes a problem involving a 5-pound bucket containing 10 pounds of water suspended from a 30-foot rope that weighs half a pound per foot. The work done in winding the rope onto a pulley to lift the bucket is calculated. The force function considers the constant weight of the bucket and the variable weight of the rope as it is wound onto the pulley. The work is calculated using a definite integral with bounds from 0 to 30 feet, resulting in 675 foot-pounds.
💧 Pumping Water from a Cylindrical Tank
The script addresses a pumping problem where water is pumped out of a cylindrical tank that is two-thirds full. The tank has a radius of 5 feet and a height of 9 feet. The work required to pump the water over the tank's rim is calculated using a formula that includes the weight density of water, the cross-sectional area of the water slices, and the distance each slice needs to be pumped. The definite integral is set up with bounds from 0 to 6 feet, and the work is found to be 56,160π foot-pounds.
🛁 Pumping Water from a Trough with Triangular Ends
The final example involves a trough that is 15 feet long and 4 feet wide at the top, with triangular ends that are 3 feet high. The trough is filled with 1 foot of water, and the work required to pump all the water over the top is calculated. Using similar triangles, a variable width for the water slices is determined, and the cross-sectional area for each slice is calculated. The work is found using a definite integral with bounds from 0 to 1 foot, resulting in 1456 foot-pounds.
Mindmap
Keywords
💡Work
💡Calculus
💡Force
💡Displacement
💡Spring Constant
💡Definite Integral
💡Foot-pounds
💡Joules
💡Pumping Problem
💡Weight Density
Highlights
Introduction to work problems solvable with calculus, emphasizing basic scenarios and formulas.
Explanation of calculating work done in lifting a bag with a constant force, using the formula work = force × displacement.
Demonstration of calculating work in lifting a 35-pound bag to a 10-foot height, resulting in 350 foot-pounds of work.
Transition to metric system for work calculation, using newtons and meters instead of pounds and feet.
Example of calculating work done pushing a truck 20 meters with a 300-newton force, equaling 6000 joules.
Introduction to variable force problems, necessitating the use of calculus and definite integrals.
Spring problem analysis involving calculating the spring constant and work done in stretching a spring.
Method to find the spring constant using force equilibrium and displacement.
Calculation of work required to stretch a spring beyond its natural length using integration.
Solving a spring problem where the work done is given to find the spring constant and new work calculations.
Propulsion problem setup using Newton's law of universal gravitation to calculate work done in space.
Detailed calculation of lifting an astronaut from the moon's surface, incorporating gravity differences.
Lifting problems involving variable forces, such as a bag of sand losing weight as it's lifted.
Derivation of a force function for a bag of sand that decreases in weight as it's lifted.
Calculation of work done in winding a rope onto a pulley, considering the variable weight of the rope.
Pumping problems overview, focusing on calculating work required to move fluids in or out of containers.
Method to calculate work in pumping water out of a cylindrical tank using the weight density of water.
Final example involving a trough with triangular ends, calculating work to pump water over the top.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: