Finding Work using Calculus - The Cable/Rope Problem - Part b

patrickJMT
2 Mar 201007:05
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, the presenter explores the concept of work required to lift a heavy rope of 60 feet in two parts. Initially, the entire 200 pounds per foot rope is lifted, requiring 3600 foot-pounds. In Part B, the focus shifts to lifting only the top half of the rope. Through a detailed explanation involving calculus, the presenter demonstrates that lifting the first half of the rope requires more work than half the total, due to the increasing force needed to overcome the weight of the entire rope. The intuitive conclusion is that lifting the first half takes 2700 foot-pounds, emphasizing the engineering implications of force distribution in lifting heavy objects.

Takeaways
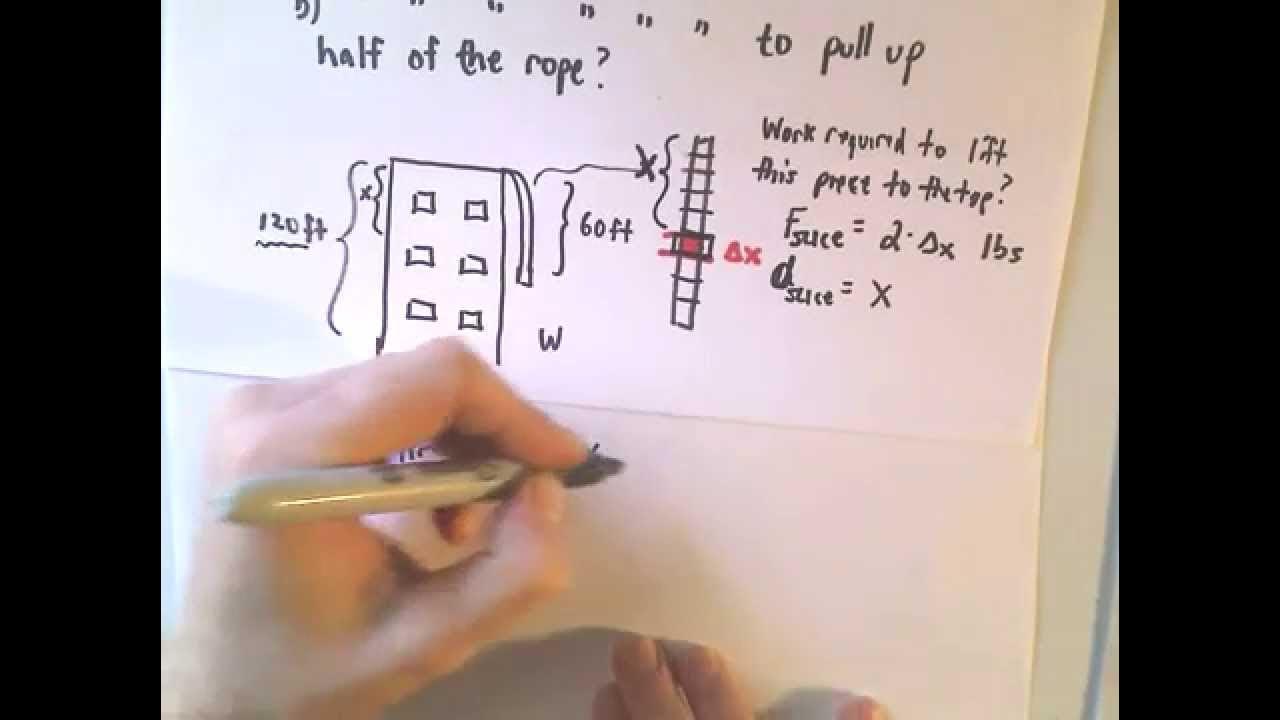
  • ๐Ÿ“ The problem involves calculating the work required to pull up half of a 60-foot long, 200 pounds per foot heavy rope hanging over a 120-foot high building.
  • ๐Ÿ”ข The total work to lift the entire rope was previously calculated to be 3600 foot-pounds.
  • ๐Ÿค” The script poses the question of whether lifting half the rope would require exactly half the work, more, or less, prompting intuitive reasoning.
  • ๐Ÿ“š The solution involves breaking the problem into two parts: calculating the work for the top half and the bottom half of the rope separately.
  • ๐Ÿ“‰ The top half of the rope (first 30 feet) is considered first, with the work calculated by integrating the force over the displacement from 0 to 30 feet.
  • ๐Ÿ“ˆ The bottom half of the rope experiences a constant force but a different displacement of 30 feet for each slice, regardless of its position.
  • โš–๏ธ The force on any slice of the rope is calculated as 2 times the differential length (2 * ฮ”X), reflecting the weight per foot.
  • ๐Ÿ“ The displacement for the top half varies with X, while for the bottom half, it is a constant 30 feet, leading to different integrals for each section.
  • ๐Ÿงฎ The integral for the top half is 2x * dx from 0 to 30, and for the bottom half, it's 60 * dx from 30 to 60, representing the work done for each section.
  • ๐Ÿ“‰ The antiderivative of 2x is x^2, and the work for the top half is calculated by evaluating this from 0 to 30, while the bottom half is a simpler calculation of 60 times the upper limit of integration.
  • ๐Ÿ”‘ The total work to lift half the rope is found to be 2700 foot-pounds, which is less than half the work required to lift the entire rope, illustrating a non-linear relationship between the amount of rope lifted and the work done.
  • ๐Ÿ’ก The script concludes with an intuitive explanation that lifting the first half of a heavy rope requires overcoming the weight of the entire rope, whereas lifting the second half involves less weight, hence less work.
Q & A

  • What is the total length of the heavy rope mentioned in the script?

    -The heavy rope mentioned in the script is 60 feet long.

  • What is the weight of the rope per foot?

    -The rope weighs 200 pounds per foot.

  • How high is the building from which the rope is hanging?

    -The building is 120 feet high.

  • What was the calculated work required to lift the entire rope in the first part of the problem?

    -The work required to lift the entire rope was calculated to be 3600 foot-pounds.

  • What is the objective of Part B of the problem?

    -The objective of Part B is to determine the work required to pull up only half of the rope.

  • Why can't the work for lifting the top and bottom halves of the rope be calculated at once?

    -The work for lifting the top and bottom halves cannot be calculated at once because the displacement for each slice of the rope varies depending on its position on the rope.

  • What is the displacement for a slice of the rope from the top half when being lifted?

    -The displacement for a slice of the rope from the top half is equal to X, where X is the distance down from the top of the building.

  • What is the displacement for a slice of the rope from the bottom half when being lifted?

    -The displacement for a slice of the rope from the bottom half is always 30 feet, regardless of its position on the rope.

  • What is the total work required to lift the first half of the rope according to the calculations in the script?

    -The total work required to lift the first half of the rope is 2700 foot-pounds.

  • Why does lifting the first half of the rope take more work than lifting the entire rope?

    -Lifting the first half of the rope takes more work because you are overcoming the weight of the entire rope, whereas when lifting the entire rope, the weight is distributed throughout the process.

  • What is the intuitive explanation for why lifting the first half of the rope takes more work than half the work of lifting the entire rope?

    -The intuitive explanation is that when lifting the first half, you are compensating for the weight of the entire rope, whereas in the latter half, much of the weight is already at the top, requiring less force to lift the remaining portion.

Outlines
00:00
๐Ÿ” Calculating Work for Lifting Half a Heavy Rope

This paragraph discusses the second part of a physics problem involving a 60-foot long, 200-pounds-per-foot heavy rope hanging over a 120-foot building. The initial problem calculated the work required to lift the entire rope, which was 3600 foot-pounds. The focus here is on calculating the work needed to lift only the top half of the rope. The speaker introduces the concept by questioning whether lifting half the rope would require exactly half the work, and then explains the process of breaking down the problem into two integrals, one for the top half and one for the bottom half of the rope. The force and displacement for each section are considered, leading to the integral calculations for the work done on each half.

05:05
๐Ÿ“š Work Comparison: Full Rope vs. Half Rope

The speaker concludes the problem by revealing that lifting the first half of the rope requires 2700 foot-pounds of work, which is less than the 3600 foot-pounds needed for the full rope. This result is counterintuitive, as lifting the first half requires more work than expected. The explanation provided is that when lifting the first half, one must overcome the weight of the entire rope, whereas for the second half, much of the weight is already lifted. The speaker uses an analogy of a very heavy cable on a tall building to illustrate this concept, emphasizing the importance of understanding these principles from an engineering perspective. The paragraph ends with an invitation for comments or questions, highlighting the speaker's desire for engagement and understanding.

Mindmap
Keywords
๐Ÿ’กWork (Physics)
In physics, 'work' is defined as the amount of energy transferred by a force acting upon an object as it moves along the direction of the force. In the context of the video, the work required to lift the rope is the energy needed to overcome gravity and the weight of the rope itself. The script discusses calculating this work in foot-pounds, which is a unit of energy in the imperial system.
๐Ÿ’กCable Rope
A 'cable rope' refers to a heavy and strong rope typically used for lifting or securing heavy loads. In the video, the rope is central to the problem being discussed, with its weight and length being key factors in determining the work required to lift it. The script describes a 60-foot long, 200-pounds-per-foot rope hanging over a building.
๐Ÿ’กBuilding Height
The 'building height' is the vertical distance from the base to the top of a structure. In the script, the building is 120 feet high, which is the reference point for calculating the work needed to lift the rope to the top, emphasizing the significance of height in the work calculation.
๐Ÿ’กFoot-Pounds
'Foot-pounds' is a unit of measurement used to express the amount of work done or energy transferred. In the video, the work required to lift the entire rope is calculated in foot-pounds, which is relevant because it quantifies the effort needed to move the rope against gravity.
๐Ÿ’กIntegral
In calculus, 'integral' refers to a concept that represents the opposite of differentiation, used to calculate the accumulated quantity of a variable over a given range. The script mentions breaking the problem into integrals to calculate the work for lifting different sections of the rope, illustrating the application of calculus in physics.
๐Ÿ’กDisplacement
'Displacement' in physics is the change in position of an object. The script discusses the displacement of different sections of the rope as they are lifted, which is crucial for determining the work done on each section because work is a product of force and displacement.
๐Ÿ’กSlice
In the context of the script, a 'slice' refers to a small, imaginary segment of the rope. The work done on each slice is calculated to understand the total work required to lift the rope. The script uses the concept of slicing to break down the problem into more manageable parts.
๐Ÿ’กForce
'Force' is any interaction that, when unopposed, will change the motion of an object. The script mentions the force on a slice of the rope, which is the weight of that slice, and is essential in calculating the work done to lift the rope.
๐Ÿ’กAntiderivative
An 'antiderivative' is a function that represents the reverse process of differentiation. In the script, the antiderivative is used to find the work done over a range of the rope's length, showing how calculus is applied to solve the problem.
๐Ÿ’กConceptual Understanding
'Conceptual understanding' refers to the ability to grasp the fundamental principles or ideas behind a subject. The script emphasizes the importance of understanding the physics concepts involved in the problem, rather than just performing calculations, to appreciate the real-world implications of lifting heavy objects.
๐Ÿ’กEngineering Perspective
The 'engineering perspective' involves approaching problems with an understanding of the practical applications and implications of solutions. The script encourages thinking about the problem from an engineering standpoint, considering the real-world scenarios where such calculations would be necessary.
Highlights

Introduction to Part B of the cable rope problem, involving lifting half of a 60-foot, 200 pounds per foot heavy rope hanging over a 120-foot building.

Calculation of the work required to lift the entire rope, which was found to be 3600 foot-pounds in Part A.

Discussion on the intuition behind whether lifting half the rope would require half the work.

Explanation of the need to break the integral into two parts due to the varying displacement of rope sections.

Description of the work required for the top half of the rope, integrating from 0 to 30 feet.

Calculation of the force on a slice of the rope and its displacement for the top half.

Explanation of the work for the bottom half of the rope, where displacement is constant at 30 feet.

Integration of the work for the bottom half of the rope, integrating from 30 to 60 feet.

Total work calculation by adding the work for both the top and bottom halves of the rope.

Derivation of the antiderivative for the work done on the top half of the rope, resulting in x squared.

Calculation of the work done on the bottom half of the rope, using a constant displacement of 30 feet.

Final calculation of the total work required to lift half the rope, which is 2700 foot-pounds.

Comparison of the work required to lift the entire rope versus half the rope, revealing that lifting half takes more than half the work.

Intuitive explanation of why lifting the first half of the rope requires more work than the last half.

Practical implications of the findings for engineering, emphasizing the importance of conceptual understanding.

Encouragement for readers to think conceptually about the problem and its engineering applications.

Invitation for readers to comment or ask questions, fostering engagement and discussion.

Transcripts

Browse More Related Video

Finding Work using Calculus - The Cable/Rope Problem

Work Done Raising a Leaky Bucket with an Integral

Leaky Bucket

Calculus Work Pump Water From a Circular Swimming Pool

Calculating Work, pumping water out of a circular swimming pool

Physics 15 Torque (18 of 25) Body Mechanics: Ex. 6, F=? on Back Muscle

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsEngineeringRope ProblemWork CalculationForce AnalysisIntegral BreakdownConceptual ThinkingEducationalProblem SolvingEngineering Intuition