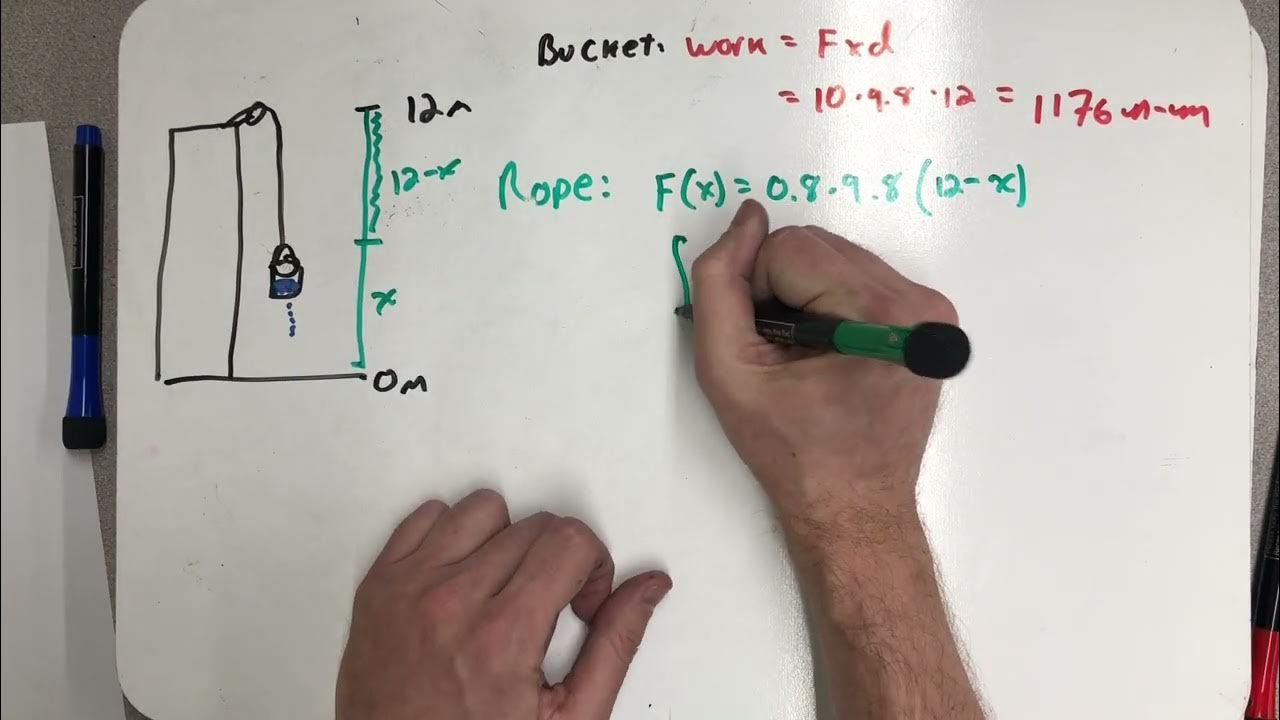
Work to lift a leaking bucket

David Lippman
30 Jun 201103:26
EducationalLearning
32 Likes 10 Comments

TLDRThe script discusses a physics problem involving a bucket with a variable mass due to a leak, complicating the work calculation. An 8-meter tall building, a negligible weight rope, and a bucket starting at 10 kg are described. As the bucket is lifted, it loses 0.5 kg for each meter, affecting the force exerted by gravity. The challenge is to calculate the work done by integrating the force over the distance, considering the changing mass from the bottom to the top of the building.

Takeaways
  • 🏢 The problem involves a building that is 8 meters tall and a bucket that starts with a mass of 10 kg.
  • 🪢 The rope's weight is negligible and not considered in the problem.
  • 🕳 The bucket has a hole and leaks 0.5 kg of material for each meter it is lifted.
  • 📉 As the bucket is lifted, its mass decreases due to the leaking material.
  • 🔢 The initial mass of the bucket is 10 kg, and it decreases linearly as it is lifted, reaching 6 kg at the top.
  • 🧲 Gravity is a factor in the problem, and the force acting on the bucket is the product of gravity and the bucket's mass.
  • 📈 The force acting on the bucket is not constant due to the changing mass as it is lifted.
  • 📚 A variable 'x' is introduced to represent the height the bucket has been lifted in meters.
  • 🔍 The remaining mass of the bucket at any height 'x' is calculated by subtracting the mass lost due to leakage from the initial mass.
  • 📝 The work done in lifting the bucket for a small distance 'dx' is the product of the force at that height and 'dx'.
  • 🧩 The total work done in lifting the bucket to the top of the building is found by integrating the work done for each small movement from the bottom to the top.
  • ∫ The integration is performed over the range from 0 to 8 meters, representing the entire height of the building.
Q & A

  • What is the height of the building mentioned in the script?

    -The building is 8 meters tall.

  • Why is the weight of the rope considered negligible in this problem?

    -The weight of the rope is considered negligible because the problem focuses on the mass and force changes of the bucket, not the rope.

  • What is the initial mass of the bucket with the sand?

    -The bucket starts with a mass of 10 kilograms.

  • How much mass does the bucket lose for every meter it is lifted?

    -The bucket loses 0.5 kilograms of sand for each meter it is lifted.

  • What is the final mass of the bucket when it reaches the top of the building?

    -By the time the bucket reaches the top, it will have lost 4 kilograms of sand, leaving it with 6 kilograms of mass.

  • What force is acting on the bucket as it is lifted?

    -Gravity is the force acting on the bucket as it is lifted, and it is dependent on the mass of the bucket.

  • How is the force on the bucket changing as it is lifted?

    -The force on the bucket is changing because the mass of the bucket is decreasing as it loses sand, making the force dependent on the height it has been lifted.

  • What variable is introduced to represent the distance the bucket has been lifted?

    -The variable 'x' is introduced to represent the distance the bucket has been lifted in meters.

  • What is the formula for calculating the remaining mass of the bucket after it has been lifted x meters?

    -The remaining mass is calculated by starting at 10 kg and subtracting 0.5 kg for each meter lifted, which is represented as 10 - (0.5 * x) kg.

  • Why is the work done on the bucket broken up into tiny movements?

    -The work is broken up into tiny movements because the force on the bucket is not constant, and it allows for the calculation of work over small distances where the force can be considered essentially constant.

  • How is the total work done on the bucket calculated?

    -The total work done on the bucket is calculated by integrating the work done over all the tiny movements from the bottom to the top of the building, which is represented by integrating from 0 to 8 meters.

Outlines
00:00
🏗️ Calculating Work with Variable Mass

The paragraph introduces a physics problem involving a variable mass scenario where the force exerted is not constant. An 8-meter tall building with a bucket attached to a rope is described. Initially, the bucket weighs 10 kg but has a hole causing it to lose 0.5 kg of sand for every meter it is lifted. This results in a decreasing force due to gravity as the bucket ascends. The concept of integrating small movements (dx) to calculate the total work done in lifting the bucket from the bottom to the top of the building is introduced, emphasizing the need to consider the variable mass over the distance.

Mindmap
Keywords
💡work problems
Work problems in physics involve scenarios where an object is moved against a force, typically gravity, and the energy required to do so is calculated. In the video's context, the complexity arises from the variable mass of the object, making the work calculation non-standard. The script discusses a bucket with a variable mass due to a leak, complicating the work done in lifting it.
💡mass
Mass is a measure of the amount of matter in an object, typically measured in kilograms. In the video, the mass of the bucket starts at 10 kg and decreases as it ascends due to the leak, making the force exerted on it change as it is lifted, which is central to the problem presented.
💡force
Force is the push or pull upon an object resulting from its interaction with another object. The video script describes how the force acting on the bucket changes as its mass decreases, emphasizing that the force is not constant throughout the lifting process.
💡gravity
Gravity is the force that attracts two objects with mass towards each other, and in this context, it is the force that the bucket must overcome to be lifted. The script mentions gravity as a factor in calculating the work done on the bucket.
💡variable
A variable is something that can change or take on different values. In the script, the mass of the bucket is variable because it decreases as sand leaks out, which is a key aspect of the problem being discussed.
💡leak
A leak refers to the unintended escape of a substance from a container. In the video, the bucket has a hole causing it to leak sand, which is a crucial element of the problem as it affects the bucket's mass and the work required to lift it.
💡integration
Integration in mathematics is a method of calculating the accumulated effect of a small change over a continuous interval. The script describes using integration to sum up the work done over the entire height of the building as the bucket is lifted, accounting for the changing mass.
💡tiny movements
Tiny movements refer to infinitesimally small increments of distance or change. The script uses the concept of lifting the bucket by an infinitesimally small amount, DX, to consider the work done over these small distances, which is then summed up through integration.
💡remaining mass
Remaining mass is the mass of an object after some of it has been lost or used up. The script calculates the remaining mass of the bucket after it has been lifted a certain height, which is essential for determining the current force acting on it.
💡distance
Distance is the measure of space between two points. In the context of the video, the distance refers to the height the bucket is lifted, which is integral to calculating the work done on the bucket as its mass changes.
💡current force
Current force refers to the force acting on an object at a specific moment or position. The script explains that the force on the bucket changes with its position as it is lifted, which is why the force is considered 'current' and dependent on the height x.
Highlights

The problem involves a scenario where the mass or force of an object is not constant, complicating the work calculation.

An 8-meter tall building is used as the context for the problem.

A rope with negligible weight is involved in the problem setup.

A bucket with an initial mass of 10 kg is at the bottom of the building.

The bucket has a hole causing it to leak 0.5 kg of sand for each meter lifted.

The force exerted on the bucket changes as it is lifted due to the loss of mass.

Gravity and mass are considered to calculate the force acting on the bucket.

A variable 'x' is introduced to represent the distance the bucket has been lifted.

The remaining mass of the bucket is calculated based on the distance lifted.

The force acting on the bucket is the product of gravity and the remaining mass.

The work done on the bucket is considered in small increments as it is lifted.

The work for a small movement is calculated using the current force and the distance moved.

The total work is obtained by integrating the work done over all small movements from the bottom to the top of the building.

Integration is used to sum up the work done over the entire lifting process.

The integration process considers the variable force due to the changing mass of the bucket.

Transcripts

Browse More Related Video

Leaky Bucket

Work Done Raising a Leaky Bucket with an Integral

Work done on lifting/falling things - Solved numerical | Work & Energy | Physics | Khan Academy

Pumping water out of a bucket, calculating work, calculus 2 tutorial

Uniform Circular Motion - 3 - Ferris Wheel

Treating systems (the hard way) | Forces and Newton's laws of motion | Physics | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics ProblemLeaking BucketVariable MassWork CalculationGravity ForceIntegrationDynamic SystemEducational ContentScience LessonMechanical WorkProblem Solving