Finding Work using Calculus - The Cable/Rope Problem
TLDRThis video tutorial demonstrates how to calculate the work required to pull a 60-foot, 2-pounds-per-foot heavy rope to the top of a 120-foot building. It breaks down the problem into an integral calculus approach, simplifying the process by dividing the rope into small segments and calculating the work needed for each. The video also poses a thought-provoking question about the work required to pull up half of the rope, challenging viewers to consider the implications of the building's height relative to the rope's length.
Takeaways
- 📚 The video is an instructional guide on solving a work-related problem involving a cable or rope.
- 🔍 The problem involves a 60-foot long rope weighing 2 pounds per foot hanging over a 120-foot building.
- 🔧 The concept of work is defined as force times displacement, and the video focuses on integrating this concept.
- 📏 The rope is divided into small segments or 'slices' to calculate the work required to lift each segment.
- 📈 The work done on each segment is modeled as an integral, with the force on the segment and its displacement as variables.
- 📐 The force on a segment is calculated by multiplying the weight per foot by the width of the segment (2 pounds per foot times delta x).
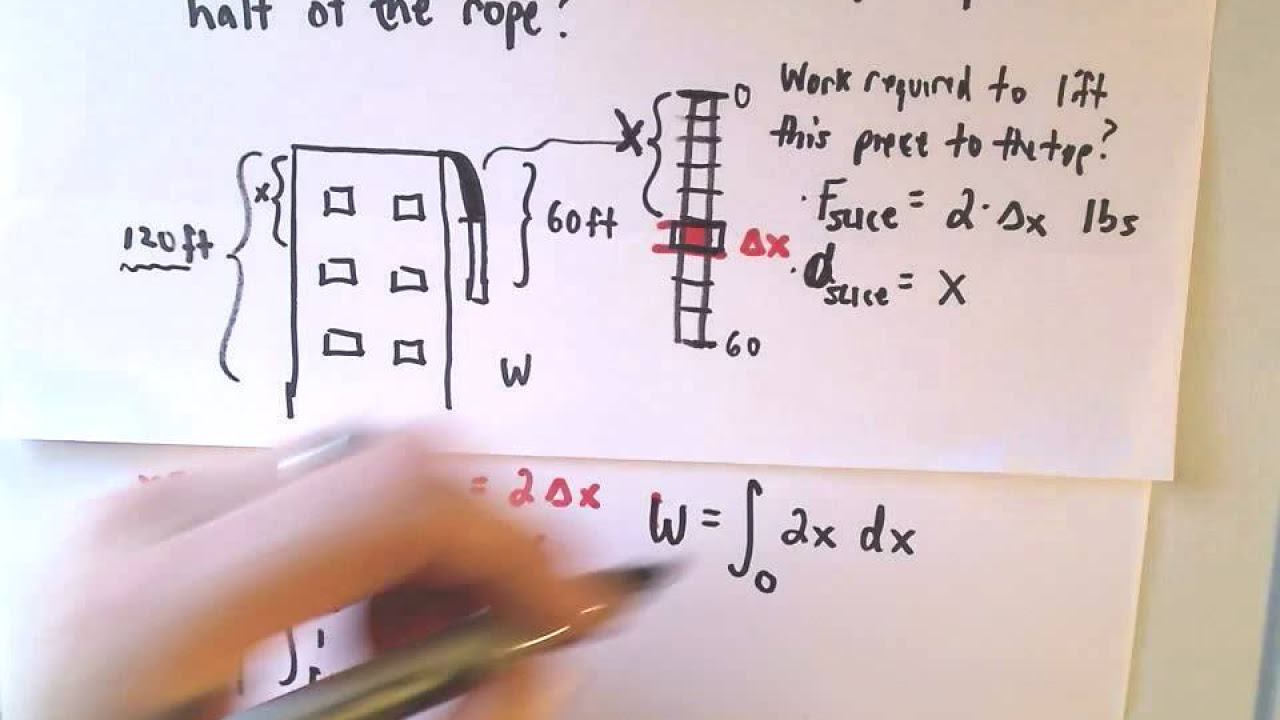
- 📉 A variable 'x' is introduced to represent the distance from the top of the building to the segment being considered.
- 🔄 The displacement for each segment is the distance 'x' it must travel to reach the top, which is also 'x'.
- 📝 The integral to solve for the total work is set up as the integral of 2x dx over the limits from 0 to 60 feet.
- 📊 The result of the integral gives the total work required to pull the entire rope to the top, which is 3600 foot-pounds.
- 🤔 Part B of the problem invites viewers to consider the work required to pull up only half of the rope and to think intuitively about the effort involved at different stages.
Q & A
What is the main topic of the video?
-The main topic of the video is to demonstrate an example of calculating work in relation to a cable and rope problem.
What are the common types of work problems mentioned in the script?
-The common types of work problems mentioned are those involving Hooke's Law and springs, cable and rope problems, and draining tank problems.
What is the definition of work given in the script?
-The definition of work given in the script is force times displacement when the force is constant.
What is the significance of the rope's weight in the problem?
-The rope's weight is significant because it determines the force acting on each segment of the rope, which is essential for calculating the work required to lift the rope.
How is the rope problem simplified in the script?
-The rope problem is simplified by dividing the rope into small segments, calculating the work required to lift each segment, and then integrating over the length of the rope.
What is the length of the rope in the problem?
-The rope is 60 feet long.
What is the weight of the rope per foot?
-The rope weighs 2 pounds per foot.
What is the height of the building in the problem?
-The building is 120 feet high.
What is the integral used to calculate the work required to pull the entire rope to the top?
-The integral used is ∫(2x) dx from 0 to 60, which simplifies to x^2 evaluated from 0 to 60.
What is the result of the integral for the work required to pull the entire rope?
-The result of the integral is 3600 foot-pounds, which is the work required to pull the entire rope to the top.
What is the purpose of introducing the variable x in the script?
-The variable x is introduced to represent the distance from the top of the building to the segment of the rope being considered, which helps in calculating the displacement for each segment.
What is the significance of the building's height in relation to the rope's length?
-The building's height is significant because it is taller than the rope, ensuring that the entire rope hangs over the edge and is relevant to the calculation of work.
What is the concept of 'lifting half of the rope' in Part B of the problem?
-The concept of 'lifting half of the rope' refers to calculating the work required to pull up only the first half of the rope's length, which is an interesting question to consider the distribution of work.
What is the intuitive question posed at the end of the script regarding lifting half of the rope?
-The intuitive question is whether it would take half as much work to lift the first half of the rope compared to the second half, or if it even matters which half is lifted first.
Outlines
🔍 Introduction to Cable Rope Work Problem
The script introduces a basic cable and rope work problem, contrasting it with more complex scenarios like Hooke's Law and springs. The presenter aims to demonstrate that such problems can be simpler than anticipated. The problem involves a 60-foot long, 2 pounds per foot heavy rope hanging over a 120-foot high building. The task is to calculate the work required to pull the rope to the top in Part A and half of the rope in Part B. The script emphasizes the building's height being greater than the rope's length, which simplifies the problem by avoiding the rope's coiling at the bottom.
📚 Calculating Work for Rope Lifting
This paragraph delves into the mathematical approach to calculate the work required to lift the rope. The presenter uses the concept of integrating the force over the displacement to find work, like finding the area under a curve with rectangles. The rope is conceptually divided into small segments, each with a force calculated by its weight per unit length. The work for each segment is then the product of this force and its displacement, which is the distance from the top of the building to the segment's starting point. The presenter introduces a variable 'x' to represent this distance and explains the process of setting up the integral with the correct limits of integration, which in this case are from 0 to 60 feet, representing the length of the rope. The integral of 2x with respect to x from 0 to 60 yields 3600 foot-pounds, which is the work required to lift the entire rope.
Mindmap
Keywords
💡Work
💡Cable and Rope Problems
💡Force
💡Displacement
💡Integral
💡Riemann Sum
💡Building Height
💡Limits of Integration
💡Foot-Pounds
💡Part A and Part B
Highlights
Introduction to a basic cable rope problem involving work calculations.
Definitions of work in terms of force and displacement, and the concept of integrating work.
Setting up the problem with a 60-foot rope weighing 2 pounds per foot hanging over a 120-foot building.
Explanation of why the building's height is relevant to the problem.
Approach to solving the problem by dividing the rope into segments and calculating work for each.
Calculating the force on a segment of the rope based on its width.
Introduction of variable 'x' to represent the distance from the top of the building to a segment of the rope.
Understanding displacement as the distance a rope segment must travel to reach the top.
Transforming the work calculation into an integral with the force and displacement.
Determining the limits of integration for the entire length of the rope.
Integration of the work function to find the total work required to pull the rope.
Result of the integration showing the work required as 3600 foot-pounds for the entire rope.
Discussion on the practical application of the work calculation in real-world scenarios.
Introduction to Part B of the problem, which involves pulling up half of the rope.
A thought experiment on the intuitive understanding of work required for pulling different sections of the rope.
Invitation for the audience to consider the implications of the building's height on the problem.
Teaser for the continuation of the problem in a follow-up video.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: