Techniques for Finding Derivatives
TLDRThe video script offers an in-depth exploration of derivative techniques, focusing on the concept of derivatives as instantaneous rates of change or slopes at any point on a curve. It introduces various notations for derivatives, such as F'(x), dy/dx, and d/dx(f(x)), emphasizing their equivalence in expressing the rate of change. The script then delves into derivative rules that simplify the process of finding derivatives, starting with the constant rule, which states that the derivative of a constant function is zero. The power rule is highlighted as a fundamental principle for differentiating polynomial functions, followed by the constant multiple rule, which allows the separation of constants when differentiating functions. The script also touches on the application of derivatives in rewriting radicals with rational exponents and handling negative exponents. Further, it covers the sum/difference rule for differentiating composite functions and illustrates how to find the slope of a tangent line at a specific point by substituting an x-value into the derivative. The concept of marginal analysis in business and economics is introduced, where derivatives are used to find rates of change in costs, revenues, and profits, with 'marginal' referring to the rate of change. Practical examples of how to derive revenue and profit functions from demand and cost functions are provided, along with calculating marginal revenue and profit at a given quantity. The script concludes by encouraging the application of these concepts in real-world scenarios, emphasizing the utility of derivatives in understanding and analyzing changes in various economic variables.
Takeaways
- 📘 The definition of a derivative is the limit of the difference quotient as H approaches zero, which represents the instantaneous rate of change or slope of a curve at a given point.
- 📚 Different notations for derivatives include F'(x), dy/dx, and d/dx(f(x)), all of which are used to represent the rate of change or slope at any point on a curve.
- 🏎️ Derivative rules are shortcuts developed from repeated use of the derivative definition, simplifying the process of finding derivatives without directly applying the limit definition.
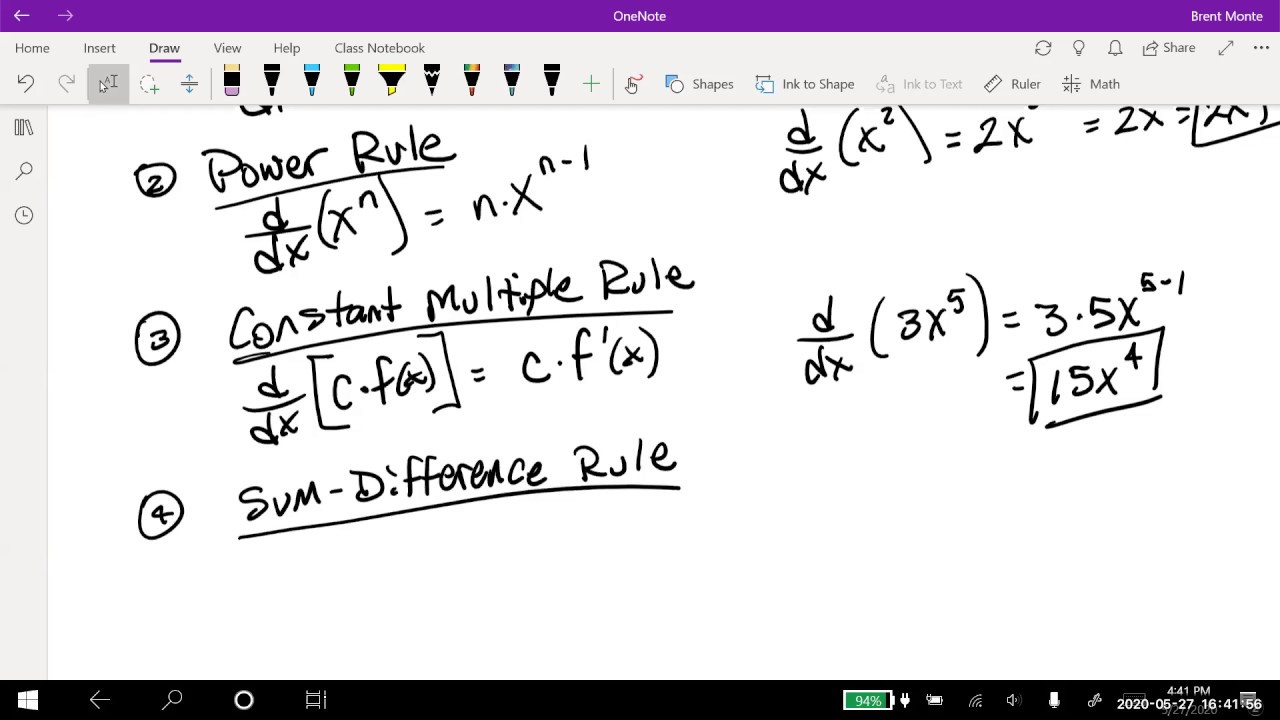
- 🅿️ The power rule states that the derivative of x to the nth power is n times x to the (n-1)th power, which simplifies finding derivatives of polynomial terms.
- 🆑 The constant rule indicates that the derivative of a constant function is always zero, as the slope of any tangent line on a constant function is horizontal.
- ✅ The constant multiple rule allows the separation of constants from functions when taking derivatives, meaning the derivative of a constant times a function is the constant times the derivative of the function.
- 🛠️ Radicals can be rewritten with rational exponents, allowing for the application of the power rule to functions involving roots.
- 🔄 The sum or difference rule states that the derivative of a sum or difference of functions is the sum or difference of the individual derivatives.
- 📈 In business and economics, the term 'marginal' refers to the rate of change, such as marginal cost, revenue, or profit, which can be found by taking the derivative of the respective functions.
- 📊 Derivatives are used to analyze various business functions like demand, cost, revenue, and profit to understand how these variables change with respect to each other.
- 📌 To find the slope of a tangent line at a specific point on a curve, plug the x value into the derivative formula to get the instantaneous rate of change at that point.
- 📉 Negative exponents can be converted to positive exponents by flipping the base to the other side of a fraction, which is a useful technique when simplifying derivatives.
Q & A
What is the definition of a derivative in terms of the limit?
-The derivative of a function f(x) is defined as the limit as h approaches 0 of the difference quotient, which is [f(x + h) - f(x)] / h.
What does the derivative of a function represent?
-The derivative of a function represents the instantaneous rate of change, or the slope of the tangent line to the curve at any given point.
What are the different notations used for derivatives in the transcript?
-The different notations for derivatives include F'(x), dy/dx, d/dx(f(x)), and df/dx.
What is the constant rule in differentiation?
-The constant rule states that the derivative of a constant function is always zero, as the slope of any tangent line on a constant (horizontal) function is zero.
How does the power rule simplify the process of finding derivatives?
-The power rule simplifies the process by stating that to find the derivative of x to the nth power, you multiply by the exponent (n) and then decrease the exponent by one.
What is the constant multiple rule in differentiation?
-The constant multiple rule states that the derivative of a constant multiplied by a function is the constant times the derivative of the function. This allows you to factor out the constant and then multiply by the result of the derivative of the function.
How can you rewrite a radical function to apply the power rule?
-A radical function can be rewritten with a rational exponent by dividing the power by the index of the radical, which then allows you to apply the power rule for differentiation.
What is the sum or difference rule for derivatives?
-The sum or difference rule states that the derivative of a sum or difference of functions is equal to the sum or difference of the individual derivatives. This means you can take the derivative of each term separately and then add or subtract them to find the overall derivative.
How can you find the slope of the tangent line at a specific point on a curve?
-To find the slope of the tangent line at a specific point, you first find the derivative of the function, which gives you the slope at any point on the curve. Then, you substitute the specific x-value into the derivative to find the slope at that point.
What is marginal analysis and how does it relate to derivatives?
-Marginal analysis is a method used in business and economics to study the rate of change of variables such as costs, revenues, and profits. The term 'marginal' refers to the rate of change, and derivatives provide these rates of change by giving the derivative of cost, revenue, or profit functions.
How are demand, revenue, cost, and profit functions related in the context of business and economics?
-In business and economics, demand functions relate the quantity of items (X) to the price (P). Revenue is the total money generated from sales, calculated as the quantity sold (X) times the price (P). Cost functions represent the expenses associated with producing or selling X items. Profit is the remaining money after subtracting the total costs from the total revenue. All these functions can be differentiated to analyze the rates at which these variables change.
Outlines
😀 Introduction to Derivatives and Notations
The video begins with an introduction to derivatives, explaining the concept as the instantaneous rate of change or slope of a curve at any given point. It emphasizes the definition of a derivative in terms of a limit, known as the difference quotient. The presenter also introduces various notations for derivatives, such as F'(x), dy/dx, and d/dx[f(x)], highlighting their equivalence and the importance of recognizing these notations. The video then transitions into discussing shortcuts or rules for finding derivatives, which are derived from repeated application of the definition, leading to patterns that simplify the process.
📚 Derivative Rules: Constant and Power Rules
The presenter explains the constant rule, which states that the derivative of a constant function is always zero, as there is no change in the slope. This is followed by the power rule, a fundamental rule for differentiating polynomial functions. The power rule involves multiplying the exponent by the variable and then decreasing the exponent by one. Several examples are provided to illustrate the application of these rules, making the process of finding derivatives more efficient and less tedious.
🔢 Constant Multiple Rule and Radical Functions
The video covers the constant multiple rule, which allows the separation of constants from functions when differentiating. It is shown that the derivative of a constant times a function is the constant times the derivative of the function. The presenter also addresses the differentiation of radical functions, demonstrating how to rewrite radicals with rational exponents to apply the power rule. This section simplifies the differentiation of complex expressions involving roots and fractions.
🔄 Sum and Difference Rule for Derivatives
The sum and difference rule is introduced, which allows for the differentiation of a sum or difference of functions by finding the derivative of each individual function and then summing or differencing the results. This rule is particularly useful for handling polynomial functions with multiple terms. The video also touches on the concept of negative exponents and their proper representation in derivatives, ensuring that the final expressions are simplified and exponents are positive.
📈 Applications of Derivatives: Marginal Analysis
The video explores the application of derivatives in business and economics, specifically in the context of marginal analysis. It explains that the term 'marginal' refers to the rate of change, such as marginal cost, revenue, or profit. Derivatives are used to find these rates of change for functions like cost, revenue, and profit. The video provides a basic example involving newspapers sold at a newsstand, showing how to derive revenue and profit functions from given demand and cost functions and how to calculate marginal revenue and profit at a specific quantity.
📚 Derivative Applications in Business and Economics
The presenter concludes with a brief overview of how derivatives are used in business and economics, emphasizing the importance of understanding rates of change, such as marginal cost, revenue, and profit. The video outlines the process of deriving revenue and profit functions from demand and cost functions and then using these to calculate marginal values at specific points. It also highlights the significance of understanding the context and units when interpreting the results of derivative calculations in real-world scenarios.
Mindmap
Keywords
💡Derivative
💡Difference Quotient
💡Limit
💡Instantaneous Rate of Change
💡Slope of a Tangent Line
💡Constant Rule
💡Power Rule
💡Constant Multiple Rule
💡Rational Exponential Form
💡Sum/Difference Rule
💡Marginal Analysis
Highlights
The definition of a derivative is introduced as the limit of the difference quotient as H approaches zero.
Derivatives are used to find the instantaneous rate of change or slope of a function at a specific point.
Different notations for derivatives are presented, including F Prime of X, d/dx y, and D/DX of f of x.
Derivative rules are shortcuts derived from repeated use of the limit definition to simplify finding derivatives.
The constant rule states that the derivative of a constant function is always zero.
The power rule is a fundamental derivative rule that applies to polynomial functions, involving multiplying by the exponent and decreasing it by one.
The constant multiple rule allows the derivative of a constant times a function to be found by multiplying the constant by the derivative of the function.
Radicals can be rewritten with rational exponents to apply the power rule for differentiation.
Negative exponents can be converted to positive exponents by flipping the base to the other side of a fraction.
The sum or difference rule for derivatives allows for the differentiation of multiple terms by taking the derivative of each term separately.
The concept of marginal analysis is introduced, relating to rates of change in business and economics.
Marginal cost, revenue, and profit are all rates of change derived from their respective functions using derivatives.
Demand, cost, revenue, and profit functions are all interconnected and can be analyzed using derivatives to understand their rates of change.
An example is provided to demonstrate how to derive revenue and profit functions from given demand and cost functions.
The marginal revenue and marginal profit are calculated for a specific quantity sold, illustrating the application of derivatives in economics.
The importance of understanding the concept of marginal in business and economics as a term for rate of change is emphasized.
Practical applications of derivatives are shown through the calculation of slopes of tangent lines and equations of tangent lines at specific points on a curve.
Graphical verification of the tangent line equation is demonstrated using a calculator, providing a method to check work.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: