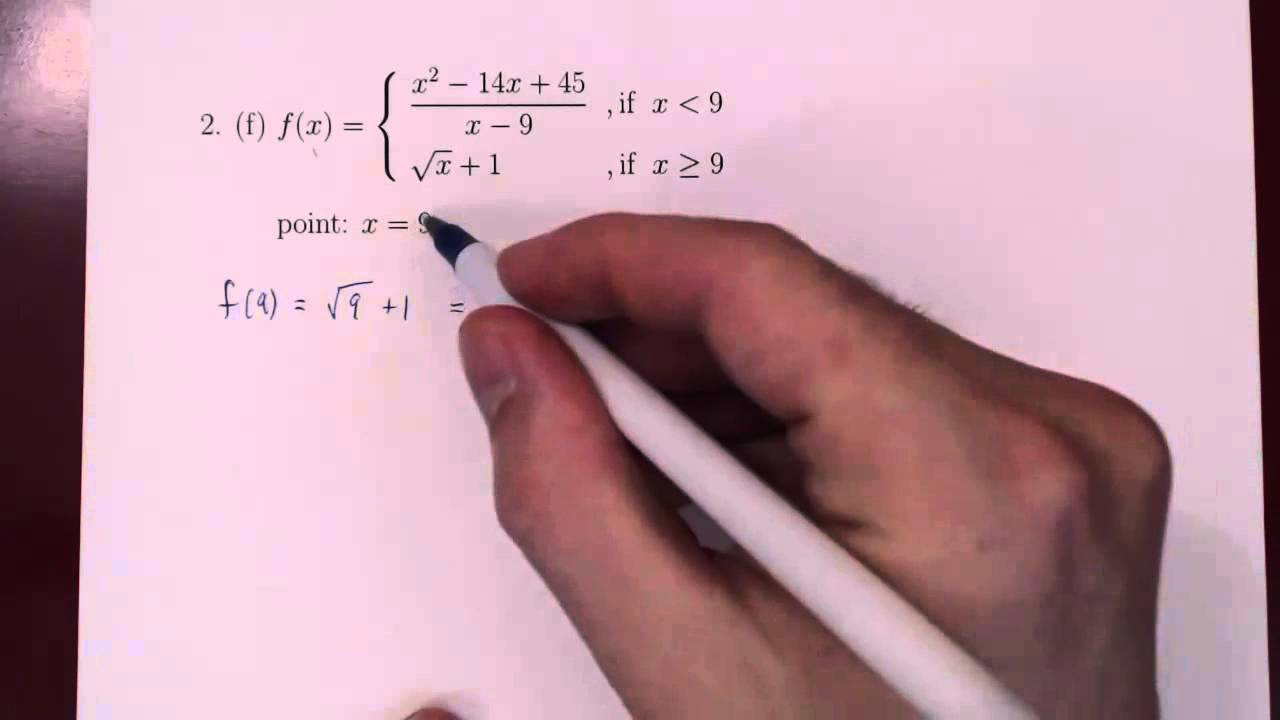BusCalc 05 Limits Examples Pt 1
TLDRIn this comprehensive video, the presenter guides viewers through a series of calculus problems focused on limits. The first example involves estimating the limit of a function as x approaches one using Microsoft Excel, which is demonstrated to approach one from both the left and right sides. The second example applies limit properties to solve a complex limit expression involving functions f(x) and g(x), resulting in the answer 9. The third example explores piecewise functions, illustrating how to graph and evaluate limits at points of discontinuity, and how to modify the function to achieve continuity. Lastly, the video covers the limit of a polynomial function as x approaches a specific value, emphasizing the continuity of polynomials and simplifying the limit to a straightforward evaluation at the given point.
Takeaways
- 📊 To estimate limits numerically, approach the limit from both sides and use tools like Microsoft Excel for a table of values and visualization.
- 🔢 When a function is undefined at a point, like ln(x)/(x-1) at x=1, evaluate the left-sided and right-sided limits to determine the two-sided limit.
- 📉 For limits involving quotients, apply the quotient rule to separate the limit into a quotient of two limits, provided the denominator's limit is not zero.
- ➖ Use the difference rule for limits to break down complex expressions into simpler parts by taking the difference of two limits.
- 📈 Recognize that constants can be factored out of limits using the product rule, simplifying the evaluation process.
- 🔁 Understand that piecewise functions can be continuous or discontinuous, depending on whether the segments connect at their endpoints.
- 📐 When graphing piecewise functions, ensure that each segment is correctly represented and that any discontinuities are clearly marked.
- 🔍 Evaluate the one-sided limits at the endpoints of a piecewise function to determine if a two-sided limit exists.
- 📉 For polynomial functions, the limit as x approaches a certain value is simply the value of the polynomial at that point, due to the continuity of polynomials.
- ✅ Given the continuity of polynomials, directly substitute the value of x into the polynomial to find the limit, avoiding unnecessary complex calculations.
- 📚 Learning and applying limit rules is crucial for solving calculus problems that involve complex limit expressions and functions.
Q & A
What is the first example problem discussed in the video?
-The first example problem is about estimating the limit as x approaches one of the function natural log(x) divided by (x - 1) using a calculator.
Why is the function undefined at x equals one in the first example?
-The function is undefined at x equals one because plugging in x = 1 results in a division by zero, which is not a real number.
How does the speaker approach estimating the limit numerically in the first example?
-The speaker uses Microsoft Excel to calculate the function's value for a sequence of numbers approaching 1 from the left and right sides to estimate the left-sided and right-sided limits.
What is the purpose of using a scatter plot in Excel as demonstrated in the video?
-The scatter plot in Excel is used to visualize the trend of the function's values as x approaches 1, helping to observe how the values are approaching a certain number.
What is the second example problem in the video about?
-The second example problem involves using limit properties to find the limit as x approaches 4 of the expression (5 times g(x) cubed minus 4) divided by (1 minus f(x)), given that the limit of f(x) as x approaches 4 is 5 and the limit of g(x) as x approaches 4 is 2.
How does the speaker apply the limit rules to solve the second example problem?
-The speaker applies the quotient rule and the difference rule for limits to break down the expression into simpler parts, then uses the given limits for f(x) and g(x) to simplify and find the final limit.
What is the third example problem in the video?
-The third example problem is about graphing and evaluating limits of a piecewise function h(x) that is defined in three different pieces based on the value of x.
How does the speaker demonstrate the graphing of the piecewise function?
-The speaker initially attempts to graph the function manually and then uses Desmos, an online graphing tool, to demonstrate the graph more professionally.
What is the significance of the right-sided and left-sided limits in the third example?
-The right-sided and left-sided limits are used to determine whether the two-sided limit exists at a particular point. If the one-sided limits do not agree, the two-sided limit does not exist at that point.
What is the fourth example problem in the video?
-The fourth example problem asks for the limit as x approaches two of the polynomial function x cubed minus three x squared plus x minus five.
Why are polynomials always continuous?
-Polynomials are always continuous because they are smooth functions without any breaks, jumps, or asymptotes, allowing for the limit to simply be the value of the polynomial evaluated at the given point.
How does the speaker calculate the limit in the fourth example?
-The speaker calculates the limit by directly substituting x with 2 in the polynomial expression and performing the arithmetic operations to find the value.
Outlines
🧮 Estimating Limits Numerically with Excel
The video begins with an introduction to solving limit problems numerically using Microsoft Excel as a substitute for a physical calculator. The first example involves finding the limit as x approaches 1 of the function ln(x)/(x-1). The presenter demonstrates that plugging in x=1 results in an undefined expression and instead shows how to calculate the left-sided limit by entering values of x that approach 1 from the left. Using Excel, a table of values is created, showing the natural logarithm of x divided by (x-1) for x values from 0.5 to 0.999. The presenter emphasizes the importance of Excel skills for business applications and shows how to create a scatter plot in Excel to visualize the approach to the limit.
📐 Limit Properties and Two-Sided Limits
The second paragraph focuses on using limit properties to solve a more complex limit problem. Given two functions f(x) and g(x) with known limits as x approaches 4, the task is to find the limit of a quotient involving these functions. The presenter applies the quotient rule and the difference rule for limits to break down the expression into simpler components. After simplifying, the presenter demonstrates how to handle constants and products within limits and uses the given information to substitute known values, ultimately finding that the limit in question is 9. The importance of understanding and applying limit rules is highlighted.
📈 Graphing and Analyzing Piecewise Functions
The third paragraph discusses the concept of piecewise functions, which are defined by different expressions over different intervals. The presenter introduces a piecewise function h(x) with three distinct pieces and explains how to graph each piece on the coordinate plane. The function is then evaluated at specific points to determine the behavior of the function and its limits as x approaches -2 and 2. The presenter uses Desmos, an online graphing tool, to visualize the function and to illustrate the concept of continuity in piecewise functions. The video also touches on how to modify a piecewise function to make it continuous.
🔍 Evaluating Limits of Polynomials
The fourth paragraph deals with finding the limit of a polynomial function as x approaches a specific value. The presenter explains that polynomials are always continuous, which means the limit of a polynomial as x approaches any value is simply the value of the polynomial at that point. The example given is to find the limit as x approaches 2 for the polynomial x^3 - 3x^2 + x - 5. By substituting x with 2, the presenter calculates the value of the polynomial at that point, resulting in a limit of -7.
Mindmap
Keywords
💡Limit
💡Natural Logarithm
💡Microsoft Excel
💡Piecewise Function
💡Continuity
💡Quotient Rule
💡Polynomial
💡Desmos
💡One-Sided Limit
💡Two-Sided Limit
💡Logarithmic Function
Highlights
The video demonstrates how to estimate limits numerically using a calculator, specifically Microsoft Excel, for the function ln(x)/(x-1) as x approaches 1.
The importance of checking both left-sided and right-sided limits to determine the existence of a two-sided limit is emphasized.
Excel is recommended for its powerful table of values and visualization features, particularly useful in a business calculus context.
The video shows how to create a scatter plot in Excel to visualize the approach of a function's output to a certain value.
Limit properties are used to find the limit of a complex function as x approaches 4, showcasing the application of limit rules.
The quotient rule for limits is applied to break apart a limit of a quotient into a quotient of two limits.
The limit of a difference is simplified into the difference of limits, illustrating the use of limit rules for algebraic manipulation.
The constant multiplier rule is applied to pull a constant outside of a limit, simplifying the expression.
The video concludes that the limit as x approaches 4 of a given function results in 9, demonstrating the successful application of limit rules.
Piecewise functions are introduced, highlighting their potential for both continuity and discontinuity at the junctions between pieces.
The video uses Desmos to graph piecewise functions professionally and to evaluate limits at specific points.
The concept of continuity in piecewise functions is explored, showing how to modify functions to ensure no discontinuities.
The limit of a polynomial as x approaches a certain value is found by simply evaluating the polynomial at that point, due to their continuous nature.
The video provides a step-by-step calculation for finding the limit of a polynomial, resulting in a value of -7.
Excel's capabilities for numerical estimation of limits and visualization of function behavior are emphasized throughout the video.
The practical application of limit concepts in calculus for business is highlighted, stressing the relevance of mathematical skills in professional contexts.
The video concludes by reinforcing the importance of understanding limit properties and their application in solving complex limit problems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: